Lesson 13
Rectangles with Fractional Side Lengths
13.1: Areas of Squares (5 minutes)
Warm-up
In this warm-up, students review how to find and record the area of a square with whole-number and fractional side lengths. The first question is open-ended to encourage students to notice many things about the area of each square, the relationships between them, and other geometric ideas they might remember from earlier grades. The second question prepares students for the work in this lesson. Focus class discussion on this question.
As students discuss the second question, note those who think of the area of a \(\frac13\)-inch square in terms of:
- Tiling, i.e., determining how many squares with \(\frac13\)-inch side length cover a square with 1-inch side length and dividing the area of 1 square inch by that number
- Multiplying \(\frac13 \boldcdot \frac13\)
Launch
Arrange students in groups of 2. Display the image and the first question for all to see. Give students 1 minute of quiet time to make observations about the squares. Follow with a brief whole-class discussion.
If not mentioned by students, ask students what they notice about the following:
- The area of each square
- How to record the area in square inches
- Whether one square could tile another square completely
Then, give students 1–2 minutes to discuss the second question with their partner.
Student Facing

- What do you notice about the areas of the squares?
- Kiran says “A square with side lengths of \(\frac13\) inch has an area of \(\frac13\) square inches.” Do you agree? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may struggle in getting started with the second question. Suggest that they try marking up the given 1-inch square to show \(\frac13\)-inch squares.
Activity Synthesis
Consider telling students that we can call a square with 1-inch side length “a 1-inch square.”
Ask previously identified students to share their response to the second question. Illustrate their reasoning for all to see. After each person shares, poll the class on whether they agree with the answer and the explanation. If not mentioned in students’ explanations, highlight the following ideas:
- A square with a side length of 1 inch (a 1-inch square) has an area of 1 in2.
- A 2-inch square has an area of 4 in2, because 4 squares with 1-inch side length are needed to cover it.
- A \(\frac12\)-inch square has an area of \(\frac14\) in2 because 4 of them are needed to completely cover a 1-inch square.
- A \(\frac13\)-inch square has a side length of \(\frac13\) inch, so it would take 9 squares to cover a 1-inch square. Its area is therefore \(\frac19\) square inch.
13.2: Areas of Squares and Rectangles (20 minutes)
Activity
This activity serves two purposes:
- To review and illustrate the idea from grade 5 that the area of a rectangle with fractional side lengths can be found by multiplying the two fractions, just as in the case of whole numbers.
- To prepare students to reason about a prism with fractional edge lengths. Students connect the area of a square with fractional side length with that of a unit square. Later, they transfer this idea to find the volume of prisms with fractional edge lengths. They will then compare whole cubic units and fractional cubic units.
As students work, monitor the ways students represent and reason about the area of the rectangle with fractional side lengths in the last question. A few possibilities are shown in the Possible Responses. Select students who use different strategies to share later.
Launch
Keep students in groups of 2. Give students 7–8 minutes of quiet work time and 2–3 minutes to share their responses and drawings with their partner. Provide each student with \(\frac14\)-inch graph paper and a straightedge.
Supports accessibility for: Organization; Attention
Student Facing
Your teacher will give you graph paper and a ruler.
-
On the graph paper, draw a square with side lengths of 1 inch. Inside this square, draw another square with side lengths of \(\frac14\) inch.
Use your drawing to answer the questions.
- How many squares with side lengths of \(\frac 14\) inch can fit in a square with side lengths of 1 inch?
- What is the area of a square with side lengths of \(\frac 14\) inch? Explain or show your reasoning.
-
On the graph paper, draw a rectangle that is \(3\frac12\) inches by \(2\frac14\) inches.
For each question, write a division expression and then find the answer.
- How many \(\frac14\)-inch segments are in a length of \(3\frac12\) inches?
- How many \(\frac14\)-inch segments are in a length of \(2\frac14\) inches?
- Use your drawing to show that a rectangle that is \(3\frac12\) inches by \(2\frac14\) inches has an area of \(7\frac78\) square inches.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have trouble counting grid squares or using a ruler on graph paper and struggle to measure the lengths of the rectangle. Consider preparing pre-drawn copies of the rectangle for students who may benefit from them.
Activity Synthesis
Focus the whole-class discussion on the last question. Invite previously selected students to share their answers and diagrams in the sequence shown in the Possible Responses. Ask students to explain how they found that \(3\frac12 \boldcdot 2\frac14\) equals \(7\frac 78 \text { in}^2\). Record their reasoning for all to see.
Consider displaying the following images and highlighting the areas of the sub-rectangles with fractional side lengths.
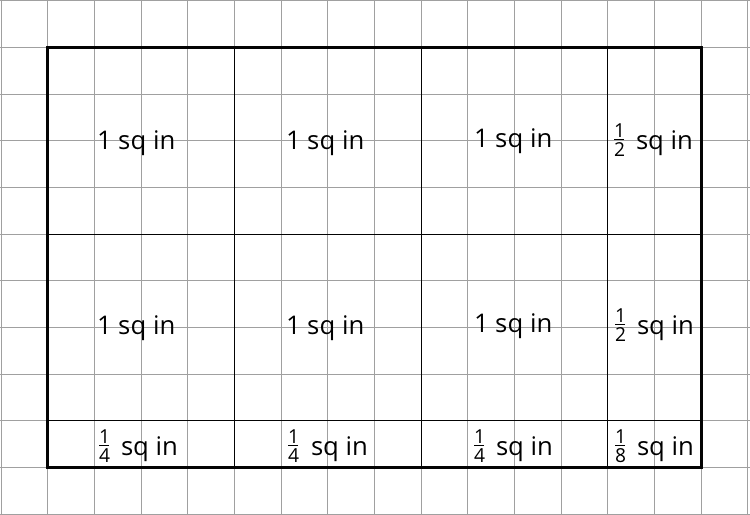
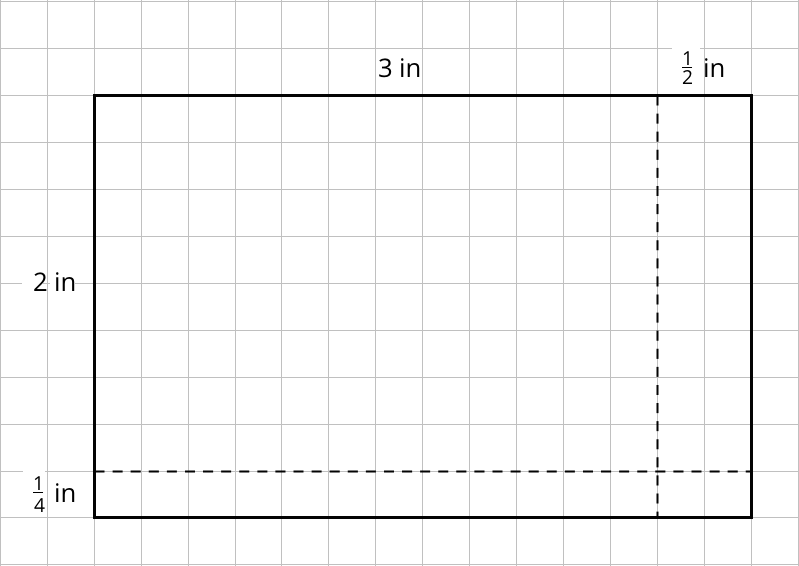
Compare and contrast the different strategies. Then, ask students how the area they found would compare to the product \(3\frac12 \boldcdot 2\frac14\). Ask them to calculate the product. Make sure students see that the product of the two numbers is equal to the area of the rectangle. \(\displaystyle 3\frac12 \boldcdot 2\frac14 = \frac72 \boldcdot \frac 94 = \frac{63}{8} = 7\frac78\)
Design Principle(s): Support sense-making; Maximize meta-awareness
13.3: Areas of Rectangles (10 minutes)
Optional activity
This activity also revisits grade 5 work on finding the area of a rectangle with fractional side lengths. Students interpret and match numerical expressions and diagrams. Because the diagrams are unlabeled, students need to use the structure in the expressions and in the diagrams to make a match (MP7). This work reinforces their understanding of the area of rectangles and of multiplication. Specifically, it helps them see how the product of two mixed numbers (or two fractions that are greater than 1) can be found using partial products.
Launch
Give students 2–3 minutes of quiet work time. Emphasize the direction that states, “All regions shaded in light blue have the same area” before students begin working.
Student Facing
Each of these multiplication expressions represents the area of a rectangle.
\(2 \boldcdot 4\)
\(2\frac12 \boldcdot 4\)
\(2 \boldcdot 4\frac 34\)
\(2\frac12 \boldcdot 4\frac34\)
-
All regions shaded in light blue have the same area. Match each diagram to the expression that you think represents its area. Be prepared to explain your reasoning.
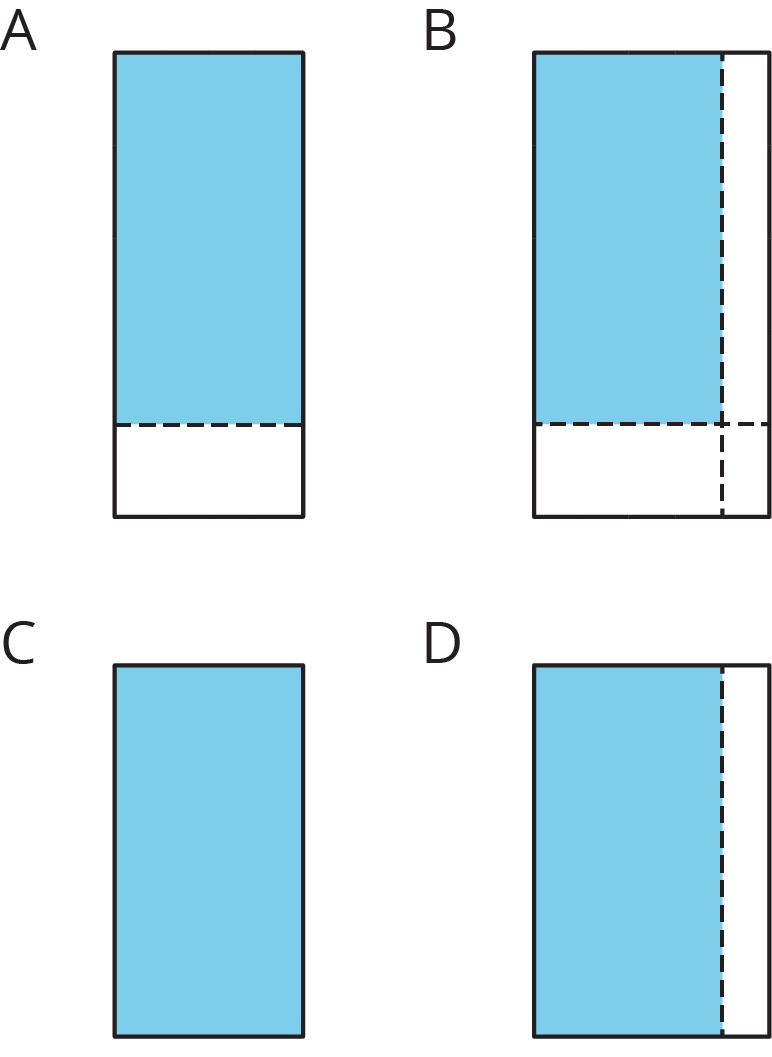
- Use the diagram that matches \(2\frac12 \boldcdot 4\frac34\) to show that the value of \(2\frac12 \boldcdot 4\frac34\) is \(11\frac78\).
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The following rectangles are composed of squares, and each rectangle is constructed using the previous rectangle. The side length of the first square is 1 unit.

-
Draw the next four rectangles that are constructed in the same way. Then complete the table with the side lengths of the rectangle and the fraction of the longer side over the shorter side.
short side long side \(\frac {\text {long side}}{\text{short side}}\) 1 1 2 3 - Describe the values of the fraction of the longer side over the shorter side. What happens to the fraction as the pattern continues?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
In answering the second question (showing that \(2\frac12 \boldcdot 4\frac34 = 11\frac78\)), some students may neglect to use the diagram and simply multiply the whole numbers in the side lengths (the 2 and 4), multiply the fractions (the \(\frac12\) and \(\frac34\)), and then add them. Allow them to pursue this path of reasoning, but later, when they recognize their answer is less than \(11\frac78\), refer them to the diagram. Ask them to identify the rectangles whose areas they have calculated and those they have not accounted for, and to think about how they could find the area of the entire rectangle.
When adding partial products with fractions in different denominators, some students may simply add the numerators and denominators. Remind them to attend to the size of the fractional parts when adding or subtracting fractions.
Activity Synthesis
For each diagram, ask one or more students to share which expression they think matches. Ask students to share their reasoning for how they matched the figure to the expression. Consider displaying the four figures for all to see and recording students’ reasoning or explanations on the figures. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
- “Do you agree or disagree? Why?”
For the second question, ask students for the area of each section in Figure B. Label each section with its side lengths and its area and display for all to see. If not already articulated by students, highlight that combining all the partial areas gives us a sum of \(11\frac78\), which is the area of the entire rectangle.
13.4: How Many Would it Take? (Part 2) (15 minutes)
Activity
This activity consolidates prior work on the area of rectangles and the current work on division of fractions. Students determine how many tiles with fractional side lengths are needed to completely cover another rectangular region that also has fractional side lengths. Besides dividing fractions, students also need to plan their approach, think about how the orientation of the tiles affects their calculation and solution, and attend carefully to the different measurements and steps in their calculation. The experience here prepares students to work with lengths and volumes in the culminating lesson (in which students determine how many small boxes with fractional edge lengths will fit into larger boxes that also have fractional edge lengths).
As students work, identify those whose diagrams or solutions show different tile orientations. Also notice students who consider both ways of laying the tiles before finding the solutions.
Launch
Keep students in groups of 2. Give students 7–8 minutes of quiet work time and 2–3 minutes to share their responses with their partner, or give 10 minutes for them to complete the activity in groups.
Design Principle(s): Support sense-making
Student Facing
Noah would like to cover a rectangular tray with rectangular tiles. The tray has a width of \(11\frac14\) inches and an area of \(50\frac58\) square inches.
- Find the length of the tray in inches.
- If the tiles are \(\frac{3}{4}\) inch by \(\frac{9}{16}\) inch, how many would Noah need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.
- Draw a diagram to show how Noah could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but does not need to show every tile.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might only determine the amount of tiles needed to line the four sides of the tray. If this happens, suggest that they look at their drawing of the tray and check whether their tiles cover the entire area of the tray.
Activity Synthesis
Invite students who chose different tile orientations to show their diagrams and explain their reasoning. Display these two diagrams, if needed.
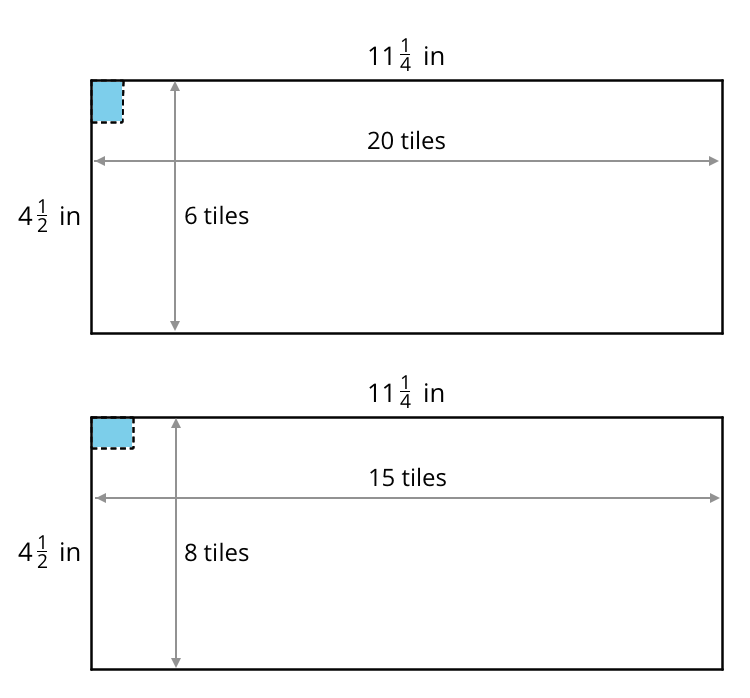
Point out how in this problem, the two different tile orientations do not matter, as the length and the width of the tiles are factors of both the length and the width of the tray. This means we can fit a whole number of tiles in either direction, and can fit the same number of tiles to cover the tray regardless of orientation.
But if the side lengths of the tiles do not both fit into \(11\frac14\) and \(4\frac12\) evenly, then the orientation of the tiles does matter (i.e., we may need more or fewer tiles, or we may not be able to tile the entire tray without gaps if the tiles are oriented a certain way).
Use the opportunity to point out that a diagram does not have to show all the details (i.e., every single tile) to be useful.
Lesson Synthesis
Lesson Synthesis
Review the different ways of reasoning about the area of a rectangle with fractional side lengths. If time permits, consider asking students to illustrate each reasoning strategy mentioned.
- “What are some ways that we can find the area of a rectangle that is \(5\frac12\) cm by \(3\frac12\) cm?” We can:
- See how many \(\frac12\)-cm squares cover the rectangle completely and multiply it by the area of each square, which is \(\frac14\) sq cm
- Decompose the rectangle into whole centimeter squares (with 1-cm side length) and other rectangles with fractional side lengths, find their areas, and add them
- Decompose the rectangle into sub-rectangles with whole-number side lengths and fractional side lengths, find their areas, and add them by multiplying the side lengths of the rectangle.
Emphasize that because we can multiply the side lengths of a rectangle (even if they are not whole numbers) to find its area, if we know the area of a rectangle and one side length, we can find the length of the other side by dividing.
- “Suppose we know that the width of a rectangle is \(4\frac35\) cm and the area is \(16\frac {1}{10}\) sq cm. How can we find its length?” (We can find \(16\frac{1}{10} \div 4\frac35 = {?}\))
- “How do we check our quotient?” (We can multiply it by the width \(4\frac35\) and see if we get the given area.)
13.5: Cool-down - Two Frames (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If a rectangle has side lengths \(a\) units and \(b\) units, the area is \(a \boldcdot b\) square units. For example, if we have a rectangle with \(\frac12\)-inch side lengths, its area is \(\frac12 \boldcdot \frac12\) or \(\frac14\) square inches.
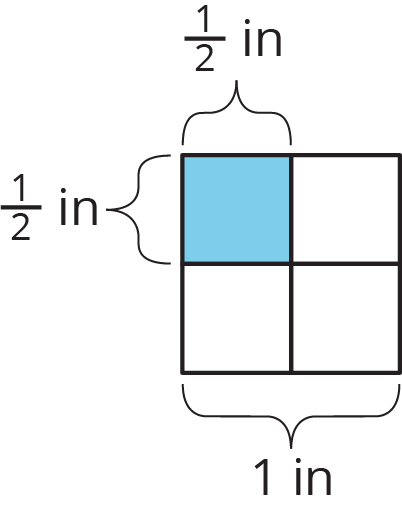
This means that if we know the area and one side length of a rectangle, we can divide to find the other side length.

If one side length of a rectangle is \(10\frac12\) in and its area is \(89\frac14\) in2, we can write this equation to show their relationship: \(\displaystyle 10\frac12 \boldcdot {?} =89\frac14\)
Then, we can find the other side length, in inches, using division: \(\displaystyle 89\frac14 \div 10\frac12 = {?}\)