Lesson 15
Volume of Prisms
15.1: A Box of Cubes (5 minutes)
Warm-up
This warm-up reviews the volume work students had done previously to prepare for the work in this lesson. It reinforces the idea of using unit cubes and fractional-unit cubes as a way to measure the volume of a rectangular prism.
Launch
Give students 2–3 minutes of quiet work time. Follow with a class discussion.
Student Facing
-
How many cubes with an edge length of 1 inch fill this box?
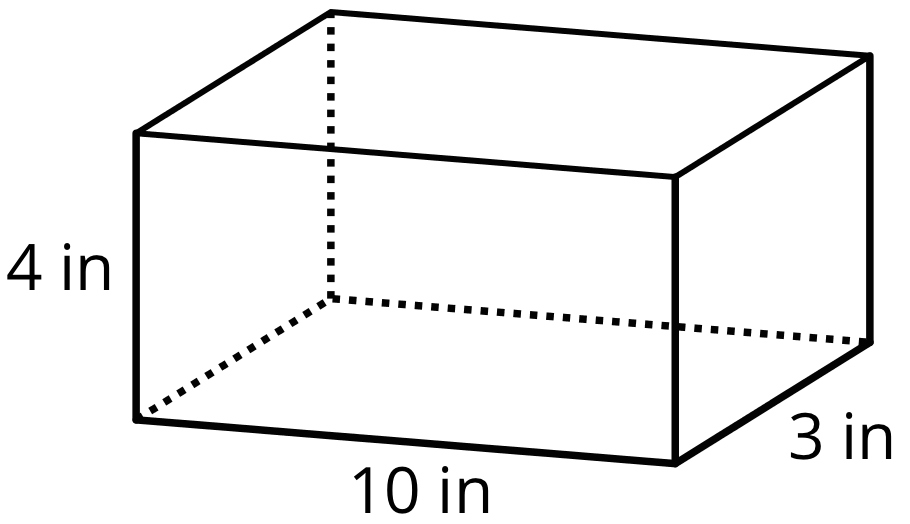
- If the cubes had an edge length of 2 inches, would you need more or fewer cubes to fill the box? Explain your reasoning.
- If the cubes had an edge length of \(\frac 12\) inch, would you need more or fewer cubes to fill the box? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select several students to share their responses and reasoning. After each person explains, ask students to indicate whether they agree. To involve more students in the discussion, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
- “Do you agree or disagree with the reasoning? Why?”
Tell students that they will use their understanding of the volume of rectangular prisms to solve other geometric problems.
15.2: Cubes with Fractional Edge Lengths (20 minutes)
Activity
In this activity, students continue the work on finding the volume of a right rectangular prism with fractional edge lengths. This time, they do so by packing it with unit cubes of different unit fractions for their edge lengths—\(\frac13\), \(\frac12\), and \(\frac14\) of an inch. They use these cubes to find the volume of the prism in cubic inches, decide which unit fraction works better to accomplish this goal and why, and explain whether cubes of different fractional edge lengths would lead to the same volume in cubic inches (MP3).
As students work, notice those who are able to clearly explain why cubes with a particular fractional edge length are preferable as a unit of measurement and why the volume in cubic inches will be the same regardless of the cubes used. Invite them to share later.
Launch
Arrange students in groups of 3–4. Give them 8–10 minutes of quiet work time, and then 5 minutes to discuss their responses with their group. Ask groups to be sure to discuss the third question. Encourage students to draw a sketch to help with reasoning, if needed.
Supports accessibility for: Memory; Conceptual processing
Student Facing
- Diego says that 108 cubes with an edge length of \(\frac13\) inch are needed to fill a rectangular prism that is 3 inches by 1 inch by \(1\frac13\) inch.
-
Explain or show how this is true. If you get stuck, consider drawing a diagram.
- What is the volume, in cubic inches, of the rectangular prism? Explain or show your reasoning.
-
-
Lin and Noah are packing small cubes into a larger cube with an edge length of \(1\frac12\) inches. Lin is using cubes with an edge length of \(\frac12\) inch, and Noah is using cubes with an edge length of \(\frac14\) inch.
- Who would need more cubes to fill the \(1\frac12\)-inch cube? Be prepared to explain your reasoning.
- If Lin and Noah each use their small cubes to find the volume of the larger \(1\frac12\)-inch cube, will they get the same answer? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students have trouble getting started, ask them to revisit their work with \(\frac12\)-inch cubes from a previous lesson. Remind them that a cube with \(\frac 12\)-inch edge length has a volume of \(\frac18\) in3 (because we can fit 8 of such cubes in a 1-inch cube). Ask them to think about how many \(\frac13\)-inch cubes can fit into a 1-inch cube, or think about what the volume of a \(\frac13\)-inch cube is in cubic inches.
Some students may not be able to visualize and keep track of the measurements of the boxes in this task. Encourage students to draw and label the measurements of the boxes described in these questions.
Activity Synthesis
Select several students to share their responses and articulate their reasoning. Compare the different strategies students used for finding the volume of the rectangular prism. Ask students:
- “Does it matter which fractional-unit cubes we use to find the volume? Why or why not?” (As long as the unit fraction can fit evenly into all three edge lengths of the prism, it doesn’t matter what unit fraction we use.)
- “Do certain unit fractions work better as edge lengths of the small cubes than others?” (It helps to use as large a unit fraction as possible, since it means using fewer cubes and working with fractions that are closer to 1.)
- “Is there another way of finding the volume of a rectangular prism with fractional edge length besides using these small cubes?” (Multiply the fractional edge lengths.)
Point out that it is helpful to use a unit fraction that is a common factor of the fractional edge lengths of the prism. Make sure students also recognize that multiplying the edge lengths of the prism is a practical way to find the volume of such a rectangular prism.
15.3: Fish Tank and Baking Pan (20 minutes)
Optional activity
In this activity, students solve word problems that involve finding the volume of rectangular prisms that have fractional edge lengths, and calculate unknown edge lengths given other measurements. The last question in the activity requires students to interpret how the same volume of liquid would fit in two different containers in the shape of rectangular prisms.
As they work, monitor for different representations students use to solve the problems.
Launch
Keep students in groups of 3–4. Give students 5 minutes of quiet work time for the first question and 2–3 minutes to discuss their responses with their group. Then, give students time to complete the second question either individually or with their group. Encourage students to draw a sketch to help with reasoning, if needed.
Supports accessibility for: Language; Conceptual processing
Student Facing
-
A nature center has a fish tank in the shape of a rectangular prism. The tank is 10 feet long, \(8\frac14\) feet wide, and 6 feet tall.
-
What is the volume of the tank in cubic feet? Explain or show your reasoning.

- The nature center's caretaker filled \(\frac45\) of the tank with water. What was the volume of the water in the tank, in cubic feet? What was the height of the water in the tank? Explain or show your reasoning.
-
Another day, the tank was filled with 330 cubic feet of water. The height of the water was what fraction of the height of the tank? Show your reasoning.
-
-
Clare’s recipe for banana bread won’t fit in her favorite pan. The pan is \(8\frac12\) inches by 11 inches by 2 inches. The batter fills the pan to the very top, and when baking, the batter spills over the sides. To avoid spills, there should be about an inch between the top of the batter and the rim of the pan.
Clare has another pan that is 9 inches by 9 inches by \(2\frac12\) inches. If she uses this pan, will the batter spill over during baking?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- Find the area of a rectangle with side lengths \(\frac12\) and \(\frac23\).
- Find the volume of a rectangular prism with side lengths \(\frac12\), \(\frac23\), and \(\frac34\).
- What do you think happens if we keep multiplying fractions \(\frac12\boldcdot \frac23\boldcdot \frac34\boldcdot \frac45\boldcdot \frac56...\)?
- Find the area of a rectangle with side lengths \(\frac11\) and \(\frac21\).
- Find the volume of a rectangular prism with side lengths \(\frac11\), \(\frac21\), and \(\frac13\).
- What do you think happens if we keep multiplying fractions \(\frac11\boldcdot \frac21 \boldcdot \frac13\boldcdot \frac41\boldcdot \frac15...\)?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite a few students to share their solutions, explanations, and drawings (if any). Record and display their solutions for all to see. To involve more students in the discussion, ask students to indicate whether they agree or disagree with their classmate’s reasoning, if they approached it the same way but could explain it differently, or if they have an alternative path.
Design Principle(s): Support sense-making; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, we used fraction multiplication and division to solve several kinds of problems about the volume of rectangular prisms. Consider using this time to help students reflect on their problem-solving process and asking questions such as:
- “How was finding the volume of a prism with fractional edge lengths like finding the volume of a prism with whole-number edge lengths? How is it different?”
- “When calculating volume, did you find it harder to work with mixed numbers than with fractions less than 1? Why or why not?” (Working with mixed numbers is a little harder since it often involves an extra step of converting them into fractions. If an error is made then, the work that follows is affected. It is easier, however, to make sense of the size of a quantity when it is written as a mixed number.)
- “How was the process of finding an unknown length of a rectangle the same or different than finding an unknown length of a prism?” (In both cases, there is one missing factor. When working with area, there are 3 quantities to keep track of: area, base, and height. When working with volume, there are 4 quantities to consider: volume, length, width, and height.)
- “Were there certain parts of calculating a volume or an unknown length that you found challenging or were prone to making mistakes? If so, which parts?”
15.4: Cool-down - Storage Box (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If a rectangular prism has edge lengths \(a\) units, \(b\) units, and \(c\) units, the volume is the product of \(a\), \(b\), and \(c\). \(\displaystyle V = a \boldcdot b \boldcdot c\)
This means that if we know the volume and two edge lengths, we can divide to find the third edge length.
Suppose the volume of a rectangular prism is \(400\frac12\) cm3, one edge length is \(\frac{11}{2}\) cm, another is \(6\) cm, and the third edge length is unknown. We can write a multiplication equation to represent the situation: \(\displaystyle \frac{11}{2} \boldcdot 6 \boldcdot {?} = 400\frac12\)
We can find the third edge length by dividing: \(\displaystyle 400\frac12 \div \left( \frac{11}{2} \boldcdot 6 \right) = {?}\)