Lesson 9
How Much in Each Group? (Part 2)
9.1: Number Talk: Greater Than 1 or Less Than 1? (5 minutes)
Warm-up
This warm-up prompts students to interpret division of fractions in terms of the number of groups of one fraction in the other (i.e., “how many groups of this in that?” question). Students do not calculate the exact value of each expression. Instead, they decide if at least one group the size of the divisor is in the dividend. This requires students to use what they know about benchmark fractions and equivalent fractions to reason about the size of the numbers.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time per problem and ask them to give a signal when they have an answer and a strategy. Follow with a whole-group discussion.
Supports accessibility for: Memory; Organization
Student Facing
Decide whether each quotient is greater than 1 or less than 1.
\(\frac12\div\frac14\)
\(1\div\frac34\)
\(\frac23\div\frac78\)
\(2\frac78\div2\frac35\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students have trouble getting started, remind them that, in a previous lesson, one way they interpreted \(4 \div \frac12 = {?}\) was as “how many \(\frac12\)s are in 4?” Ask them if that interpretation could apply here. Also encourage students to recall how the size of the divisor affects the quotient.
Some students may struggle with the last expression because they don’t easily see the relationship between fifths and eighths. Ask if they can think of a fraction, in eighths, that is close to \(\frac35\), or a fraction in fifths that is close to \(\frac78\). If not, ask them how they would reason about the expression if it was \(2\frac68\) instead of \(2\frac35\).
Activity Synthesis
Ask students to share their reasoning after completing each problem and before they think about the next problem. Record and display their explanations for all to see.
Students may reason about the answers by thinking about the relative sizes of the two fractions, which is a valid approach. This shows an understanding of how the size of the dividend and that of the divisor affect the quotient.
To encourage students to connect the division expressions to multiplication, however, ask students to support their response to each of the first two problems with a related multiplication expression or equation, or in terms of equal-sized groups. For example, \(\frac12\div\frac14\) could be connected to \({?} \boldcdot \frac14 = 2\), or the question “how many \(\frac14\)s are in \(\frac12\)?”.
To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone think about the expression the same way but would explain it differently?”
- “Did anyone find the value in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
- “Do you agree or disagree? Why?”
Design Principle(s): Optimize output (for explanation)
9.2: Two Water Containers (15 minutes)
Activity
This activity prompts students to solve a problem involving division of fractions in a less-scaffolded way. Students can see two relevant numbers to work with, but they need to interpret the context, the visual information, and the written question to decide whether the missing value is the size of one group, the number of groups, or the given amount (MP1). By carefully making sense of the context, students see that part of a group is known and they have to find the size of the whole group.
As students work, monitor the strategies they use and the way they reason about the situation. Students may draw directly on the photo to make sense of the quantities. Some may draw a tape diagram or another type of diagram to represent the partially-filled water container. Others may bypass diagramming and instead reason verbally or by writing equations. Select a few students who use different but equally effective strategies to share later.
Launch
Arrange students in groups of 3–4. Show the short video. Ask students what questions we could ask about the amount of water in this situation that would require working with fractions to determine the answers. Give groups a moment to think about their questions. If needed, show the video again, or refer to the photos to identify the fractions.
Possible questions:
- How much water fits into the whole water dispenser?
- How much water is indicated by each tick mark of the water dispenser?
- How far would 1 liter of water fill the water dispenser?
After hearing students’ ideas, give students 4–5 minutes of quiet work time and then another 2 minutes to share their responses with their group. Ask students to discuss any disagreements they might have about their interpretation of the problem, the solving process, or the answer. Remind students they can check their solution using the multiplication equation.
Supports accessibility for: Memory; Organization
Student Facing

- After looking at these pictures, Lin says, “I see the fraction \(\frac 25\).” Jada says, “I see the fraction \(\frac 34\).” What quantities are Lin and Jada referring to?
-
Consider the problem: How many liters of water fit in the water dispenser?
-
Write a multiplication equation and a division equation for the question.
-
Find the answer and explain your reasoning. If you get stuck, consider drawing a diagram.
-
Check your answer using the multiplication equation.
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
For the second question, students may not immediately see that, to answer the question “how many liters of water fit in the dispenser?” they need to relate the amount in liters (as shown in the measuring cup) to the fraction of the dispenser that is filled with water. Suggest that they think about the problem in terms of equal-sized groups and try to identify the groups, number of groups, etc.
Activity Synthesis
Invite previously identified students to share their solutions and reasoning. Sequence their presentations so that the more concrete strategies are presented before the more abstract (e.g., a student who used only equations should present last). Display their diagrams and record their reasoning for all to see.
Connect the reasoning done using the diagram to the mathematical operations. Regardless of the path students took, finding the amount of water that fills the entire dispenser requires dividing \(\frac34\) liters by 2 (to find the amount in \(\frac15\) of a dispenser), and then multiplying that amount by 5. Consider revisiting this activity later, after students have learned an algorithm for dividing a fraction, and using this problem to reinforce that multiplying by the denominator and dividing by the numerator makes sense as a way to divide by a fraction.
9.3: Amount in One Group (15 minutes)
Activity
In this activity, students practice reasoning about the amount in one group in division situations. They continue to write equations and draw diagrams to support their reasoning. In two problems (odd-numbered), the given number of groups is greater than 1. In the other two problems (even-numbered), a fraction of a group is given. Though this does not affect the structure of the equations students write, students need to take care to reflect this information correctly in their diagrams.
Students choose two problems to solve and work in groups of 2. Time permitting, students create a visual display of their work and conclude the activity with a gallery walk.
Launch
Arrange students in groups of 2. Ask each group to choose two problems: an even-numbered problem and an odd-numbered problem. Give students 7–8 minutes of quiet time to work on their two chosen problems, and a few minutes to share their work with their partner.
Provide access to geometry toolkits and tools for creating a visual display. If time permits, ask each group to create a visual display of their solution and reasoning for one problem. Emphasize that they should organize their reasoning so it can be followed by others.
Supports accessibility for: Visual-spatial processing; Organization
Student Facing
Write a multiplication equation and a division equation and draw a diagram to represent each situation. Then, find the answer and explain your reasoning.
-
Jada bought \(3\frac12\) yards of fabric for $21. How much did each yard cost?
-
\(\frac 49\) kilogram of baking soda costs $2. How much does 1 kilogram of baking soda cost?
-
Diego can fill \(1\frac15\) bottles with 3 liters of water. How many liters of water fill 1 bottle?
-
\(\frac54\) gallons of water fill \(\frac56\) of a bucket. How many gallons of water fill the entire bucket?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The largest sandwich ever made weighed 5,440 pounds. If everyone on Earth shares the sandwich equally, how much would you get? What fraction of a regular sandwich does this represent?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Arrange for groups that are assigned the same problem to present their visual displays near one another. Give students a few minutes to visit the displays and to see how others reasoned about the same two problems they chose. Before students begin a gallery walk, ask them to be prepared to share a couple of observations about how their strategies and diagrams are the same as or different from others’.
After the gallery walk, invite a couple of students to share their observations. Tell them that, in upcoming lessons, they will investigate other ways to reason efficiently about division problems.
Design Principle(s): Optimize output (for explanation)
9.4: Inventing Another Situation (15 minutes)
Optional activity
This open-ended activity gives students a chance to formulate their own scenarios for a division expression, find the value of that expression, and make sense of the value in the context of their scenario (MP2).
By now students will have seen a variety of situations in which a division means finding “how many groups of this in that?” or finding “how much in each group?” and can refer to these two interpretations of division to get started. If they are stuck, encourage them to consult the examples they have seen so far (e.g., the problems about the water container, the lengths of ropes, cleaning the highway, etc.)
As students work, notice the different types of problems students are writing, the range of attributes (length, volume, weight, etc.) involved, the different types of diagrams used, and the interpretation of division chosen (number of groups vs. size of a group). Select a couple of students who interpret the expression in different ways to share later.
Launch
Arrange students in groups of 4. If desired, arrange students in groups of 4 in two dimensions. (Assign each student into a group, and then to a label within it, so that new groups—consisting of one student from each of the original groups—can be formed later.) Provide continued access to tools for creating a visual display.
Give students 4–5 minutes of quiet think time to invent a scenario and a question. Then, before they find the answer to the question, ask them to trade their scenarios with a person in their group, give each other feedback about how well the question fits the expression, and revise the question. When they are ready, ask them to write their question on the visual display.
Design Principle(s): Support sense-making
Student Facing
- Think of a situation with a question that can be represented by \(\frac{1}{3}\div\frac14 = {?}\). Describe the situation and the question.
-
Trade descriptions with a partner.
- Review each other’s description and discuss whether each question matches the equation.
- Revise your description based on the feedback from your partner.
- Find the answer to your question. Explain or show your reasoning. If you get stuck, consider drawing a diagram.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Consider rearranging students into new groups of 4 so they can share their questions and solutions in small groups.
If possible, select one person who came up with a “\(\frac 14\) of what number is \(\frac 13\)?” type of question, and another who wrote a “how many \(\frac14\)s in \(\frac13?\)” type of question to share their questions and explain their solution paths to the class.
If needed, use these examples to illustrate two different interpretations of the division statement.
- First interpretation: If \(\frac13\) liter fills \(\frac14\) of a bottle, how many liters fill 1 bottle?
- Second interpretation: If 1 bottle contains \(\frac14\) liter of water, how many bottles can be filled with \(\frac 13\) liter of water?
In this case, students will likely find the first interpretation of division easier to represent and to solve using a diagram.
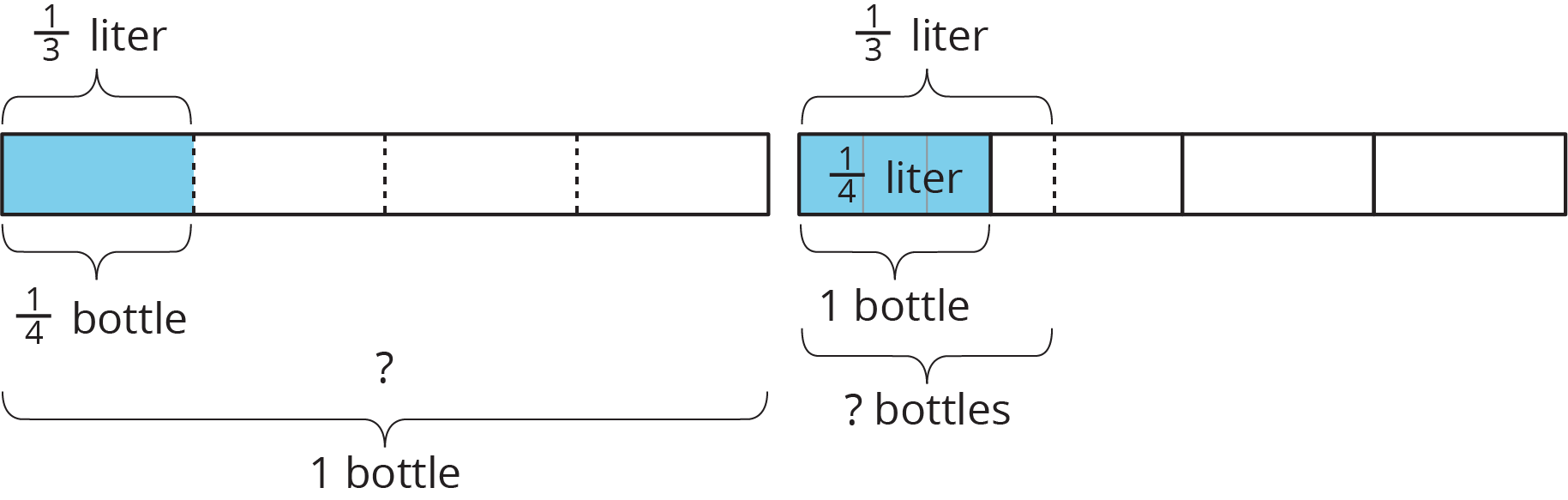
The diagram on the left shows the content of \(\frac14\) of a bottle, which is \(\frac 13\) liter, being multiplied by 4 to get the content of 1 bottle, which is \(\frac 43\) liters. The diagram on the right shows that 1 bottle contains \(\frac14\) liter, or 3 parts of \(\frac {1}{12}\) liter. In \(\frac13\) liter there are 4 parts of \(\frac {1}{12}\), so \(\frac13\) liter fills \(1\frac13\) bottles.
Lesson Synthesis
Lesson Synthesis
In this lesson, we solved problems that involved finding the amount in one group. Present this problem and give students a minute of quiet think time: How long is a whole trip if \(\frac23\) of a trip is \(\frac45\) mile? Then, discuss some of the following questions.
-
“What is the ‘one group’ we are interested in here?” (One full trip.)
-
“Do we know the number of groups or the fraction of a group?” (Yes, \(\frac23\) of a group.)
-
“What multiplication equation and division equations can we write to represent this situation?” (\(\frac23 \boldcdot {?} = \frac45\) and \(\frac 45 \div \frac23 = {?}\))
-
“How can we interpret \(\frac23 \boldcdot {?} = \frac45\)? in this context?” (We can think of it as asking “\(\frac23\) of what distance is \(\frac45\) mile?”)
-
“How might we set up a tape diagram to help us answer the question?” (The tape should show two rectangles to represent \(\frac23\) of a trip and \(\frac45\) mile, which allows us to see \(\frac13\) of the trip as \(\frac25\) mile and the whole trip as \(3 \boldcdot \frac25\) or \(\frac65\) miles.)
Explain to students that sometimes it is not always obvious whether a division situation involves finding the number of groups or the size of 1 group. There may be two 1 wholes to keep track of and two possible questions that could be asked. We need to analyze the situation carefully to reason correctly.
9.5: Cool-down - Refilling a Soap Dispenser (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes we have to think carefully about how to solve a problem that involves multiplication and division. Diagrams and equations can help us.
For example, \(\frac34\) of a pound of rice fills \(\frac25\) of a container. There are two whole amounts to keep track of here: 1 whole pound and 1 whole container. The equations we write and the diagram we draw depend on what question we are trying to answer.
-
How many pounds fill 1 container?
\(\displaystyle \frac 25 \boldcdot {?} = \frac 34\)
\(\displaystyle \frac 34 \div \frac 25 = {?}\)
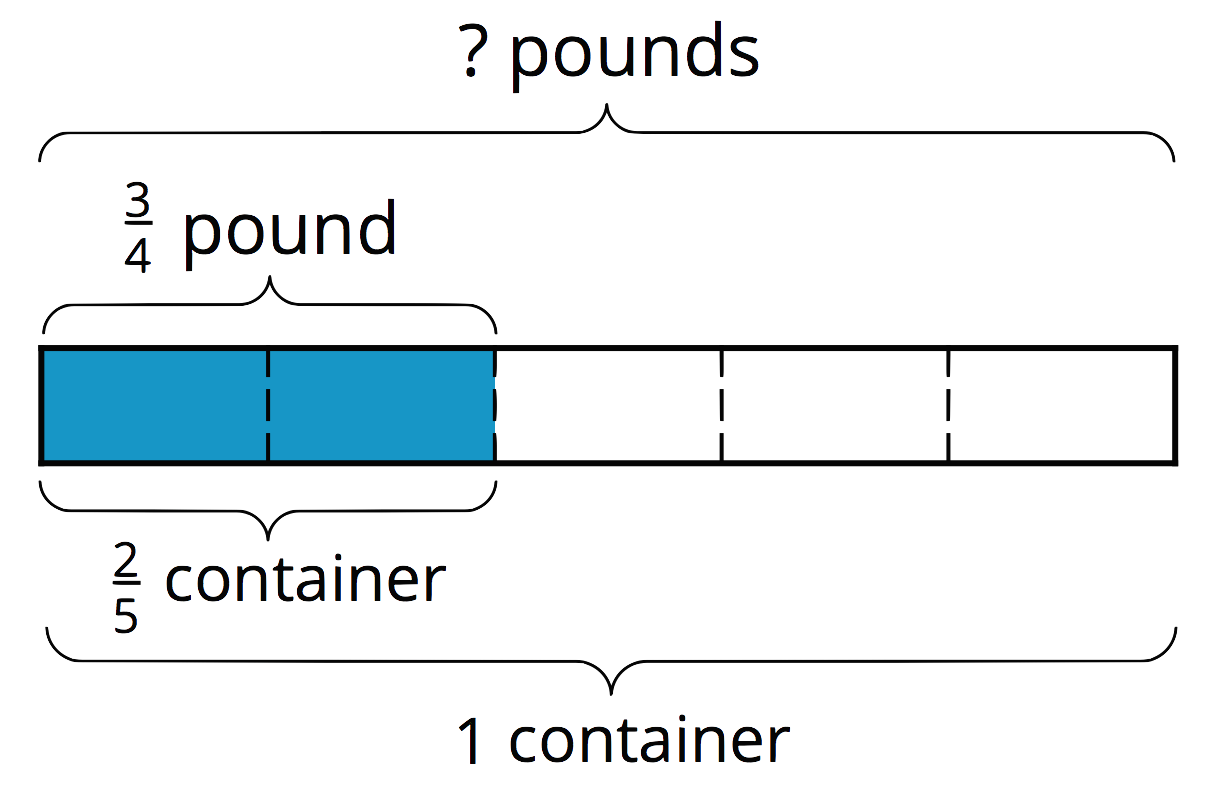
If \(\frac25\) of a container is filled with \(\frac 34\) pound, then \(\frac 15\) of a container is filled with half of \(\frac34\), or \(\frac38\), pound. One whole container then has \(5 \boldcdot \frac38\) (or \(\frac {15}{8}\)) pounds.
-
What fraction of a container does 1 pound fill?
\(\displaystyle \frac34 \boldcdot {?} = \frac25\)
\(\displaystyle \frac25 \div \frac34 ={?}\)
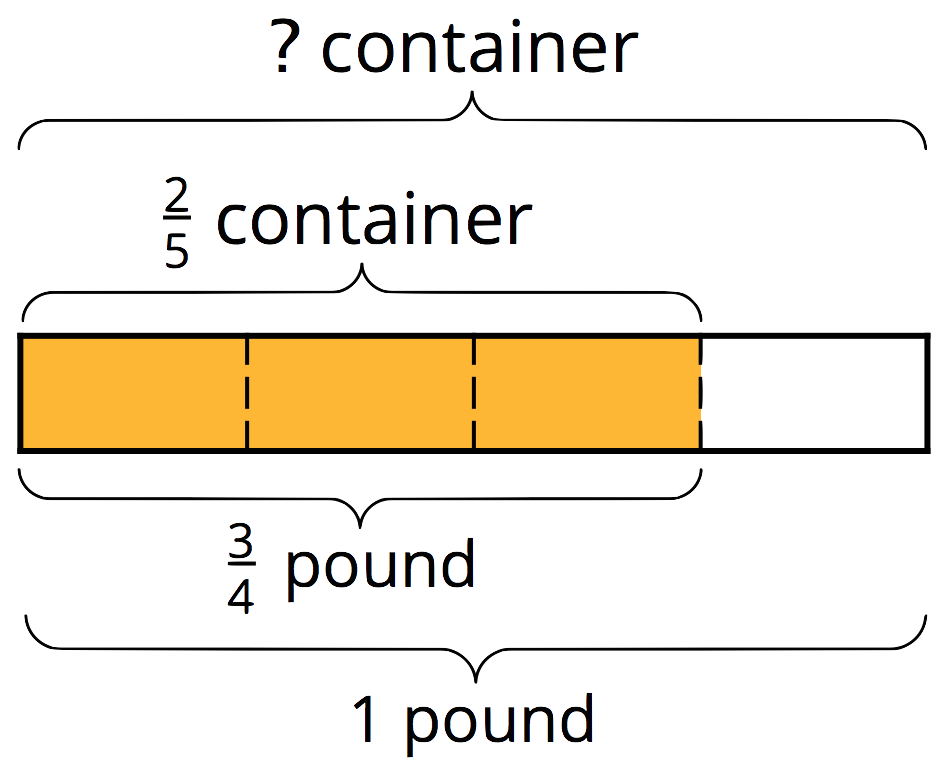
If \(\frac 34\) pound fills \(\frac25\) of a container, then \(\frac14\) pound fills a third of \(\frac25\), or \(\frac {2}{15}\), of a container. One whole pound then fills \(4 \boldcdot \frac{2}{15}\) (or \(\frac {8}{15}\)) of a container.