Lesson 14
Fractional Lengths in Triangles and Prisms
14.1: Area of Triangle (5 minutes)
Warm-up
This warm-up allows students to review calculation of triangular area and prepares them to use division of fractions to solve area problems involving triangles later. Students calculate the area of a triangle given fractional base and height measurements.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet work time, followed by 1 minute of partner discussion. Before students begin, review the formula for the area of a triangle. Consider displaying a drawing of a triangle with one side labeled as a base and a corresponding height shown and labeled as such.
Student Facing
Find the area of Triangle A in square centimeters. Show your reasoning.
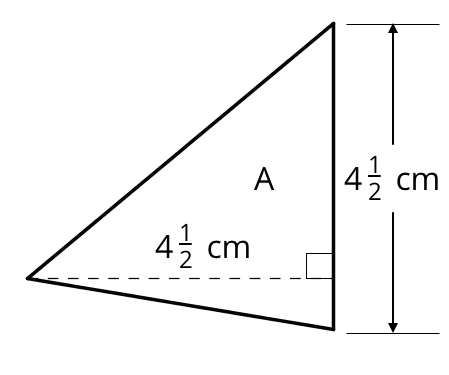
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask a student to share their solution and reasoning. Record it for all to see. Poll the class to see whether students agree or disagree. Ask if others had alternative ways of reasoning or calculating.
Tell students that they will solve more problems involving the area of triangles in this lesson.
14.2: Bases and Heights of Triangles (10 minutes)
Activity
In this activity, students apply their knowledge of division of fractions to answer questions about bases and heights of triangles, which they studied earlier in the year. In the warm-up, students recalled how to find the area of a triangle given a pair of base and height. Here, they find a missing length given the area of a triangle and a fractional base or height.
The formula for the area of a triangle \(A = \frac12 \boldcdot b \boldcdot h\) presents a different multiplication situation than students have seen in this unit—there are three factors at play. Students are likely to approach in a number of ways. They may:
- Draw a duplicate of the triangle and compose a parallelogram with the same base and height, double the given area (to represent the area of the parallelogram), and then divide by the known length to find the unknown length
- Without drawing, multiply the given area by 2 to find the value of \(b \boldcdot h\), and then divide it by the known length
- Perform division twice, i.e., dividing the area by \(\frac12\) and then by the known base or length, or vice versa
- Multiply the known length and \(\frac12\) first, so there are only two factors to work with (e.g., for \(\frac12 \boldcdot b \boldcdot \frac83 = 8\), they may apply the commutative and associative properties of operations and write \(\frac12 \boldcdot \frac83 \boldcdot b = 8\) and then \(\frac43 \boldcdot b = 8\))
Monitor for these or other approaches as students work. Select students who use different strategies to share later.
Launch
Keep students in groups of 2. Give students 4–5 minutes of quiet work time and 2 minutes to discuss their responses and complete the activity with their partner. Keep the formula for the area of a triangle and a labeled drawing of a triangle displayed.
Supports accessibility for: Memory; Language
Student Facing
-
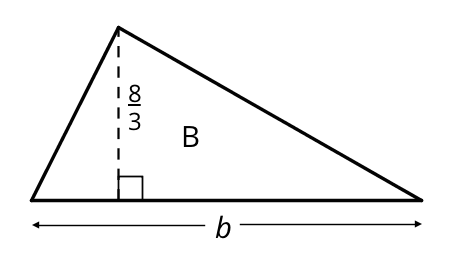
The area of Triangle B is 8 square units. Find the length of \(b\). Show your reasoning.
-
The area of Triangle C is \(\frac{54}{5}\) square units. What is the length of \(h\)? Show your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not know how to find a missing factor when three—instead of two—factors are involved. Ask if there is any step to take or any calculation to make first so they are only working with two factors.
Activity Synthesis
Ask previously selected students to share their solutions and reasoning. Sequence their presentations so that students who reasoned concretely (e.g., by duplicating the triangle to compose a parallelogram) present first and those who reasoned symbolically (e.g., only by manipulating expressions or equations) present last. After each student shares, ask all students to indicate whether they reasoned the same way.
Clarify that there is no single way to solve problems such as these. Point out specific points in the solving process where division of fractions enabled them to complete their reasoning. Emphasize that what we learned about fractions and operations in this unit can help us reason more effectively about problems in other areas of mathematics.
Design Principle(s): Optimize output (for explanation)
14.3: Volumes of Cubes and Prisms (20 minutes)
Activity
This activity extends students’ understanding about the volume of rectangular prisms from earlier grades. Previously, students learned that the volume of a rectangular prism with whole-number edge lengths can be found by computing the number of unit cubes that can be packed into the prism. Here, they draw on the same idea to find the volume of a prism with fractional edge lengths. The edge length of the cubes used as units of measurement are not 1 unit long, however. Instead, they have a unit fraction (\(\frac 12\), \(\frac 14\), etc.) for their edge length. Students calculate the number of these smaller cubes in a prism and use it to find the volume in a standard unit of volume measurement (cubic inches, in this case).
By reasoning repeatedly with small cubes (with \(\frac12\)-inch edge lengths), students notice that the volume of a rectangular prism with fractional edge lengths can also be found by directly multiplying the edge lengths in inches.
Launch
Tell students to look at the image of the 1-inch cube in the task (or display it for all to see). Ask students:
- “This cube has an edge length of 1 inch. What is its volume in cubic inches?” (1 cubic inch.) “How do you know?” (\(1 \boldcdot 1 \boldcdot 1 = 1\))
- “How do we find the volume of a cube with an edge length of 2 inches?” (\(2 \boldcdot 2 \boldcdot 2 = 8\). Or, since we can pack it with eight 1-inch cubes, we can tell its area is \(8 \boldcdot 1\) or 8 cubic inches.)
If no students mentioned using the 1-inch cube to find the volume of the 2-inch cube, bring it up. Consider telling students that we can call a cube with edge length of 1 inch a “1-inch cube.”
Arrange students in groups of 3–4. Give each group 20 cubes and 5 minutes to complete the first set of questions. Ask them to pause for a brief class discussion afterwards.
Invite students to share how they found the volume of a cube with \(\frac12\)-inch edge length and the prism composed of 4 stacked cubes. For the \(\frac12\)-inch cube, if students do not mention one of the two ways shown in the Possible Responses, bring it up. For the tower, if they don’t mention multiplying the volume of a \(\frac12\)-inch cube, which is \(\frac18\) cubic inch, ask if that is a possible way to find the volume of the prism.
Next, give students 7–8 minutes to complete the rest of the activity.
For classes using the digital materials, an applet is provided, but using physical cubes is preferred and recommended. Adapted from an applet made in GeoGebra by Susan Addington.
Design Principle(s): Support sense-making
Student Facing
Use cubes or the applet to help you answer the following questions.
-
Here is a drawing of a cube with edge lengths of 1 inch.
- How many cubes with edge lengths of \(\frac12\) inch are needed to fill this cube?
- What is the volume, in cubic inches, of a cube with edge lengths of \(\frac12\) inch? Explain or show your reasoning.

- Four cubes are piled in a single stack to make a prism. Each cube has an edge length of \(\frac12\) inch. Sketch the prism, and find its volume in cubic inches.
-
Use cubes with an edge length of \(\frac12\) inch to build prisms with the lengths, widths, and heights shown in the table.
-
For each prism, record in the table how many \(\frac12\)-inch cubes can be packed into the prism and the volume of the prism.
prism
length (in)prism
width (in)prism
height (in)number of \(\frac12\)-inch
cubes in prismvolume of
prism (in3)\(\frac12\) \(\frac12\) \(\frac12\) 1 1 \(\frac12\) 2 1 \(\frac12\) 2 2 1 4 2 \(\frac32\) 5 4 2 5 4 \(2\frac12\) - Examine the values in the table. What do you notice about the relationship between the edge lengths of each prism and its volume?
-
- What is the volume of a rectangular prism that is \(1\frac12\) inches by \(2\frac14\) inches by 4 inches? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Tell students to look at the image of the 1-inch cube in the task (or display it for all to see). Ask students:
- “This cube has an edge length of 1 inch. What is its volume in cubic inches?” (1 cubic inch.) “How do you know?” (\(1 \boldcdot 1 \boldcdot 1 = 1\))
- “How do we find the volume of a cube with an edge length of 2 inches?” (\(2 \boldcdot 2 \boldcdot 2 = 8\). Or, since we can pack it with eight 1-inch cubes, we can tell its area is \(8 \boldcdot 1\) or 8 cubic inches.)
If no students mentioned using the 1-inch cube to find the volume of the 2-inch cube, bring it up. Consider telling students that we can call a cube with edge length of 1 inch a “1-inch cube.”
Arrange students in groups of 3–4. Give each group 20 cubes and 5 minutes to complete the first set of questions. Ask them to pause for a brief class discussion afterwards.
Invite students to share how they found the volume of a cube with \(\frac12\)-inch edge length and the prism composed of 4 stacked cubes. For the \(\frac12\)-inch cube, if students do not mention one of the two ways shown in the Possible Responses, bring it up. For the tower, if they don’t mention multiplying the volume of a \(\frac12\)-inch cube, which is \(\frac18\) cubic inch, ask if that is a possible way to find the volume of the prism.
Next, give students 7–8 minutes to complete the rest of the activity.
For classes using the digital materials, an applet is provided, but using physical cubes is preferred and recommended. Adapted from an applet made in GeoGebra by Susan Addington.
Design Principle(s): Support sense-making
Student Facing
Your teacher will give you cubes that have edge lengths of \(\frac12\) inch.
-
Here is a drawing of a cube with edge lengths of 1 inch.

- How many cubes with edge lengths of \(\frac12\) inch are needed to fill this cube?
-
What is the volume, in cubic inches, of a cube with edge lengths of \(\frac12\) inch? Explain or show your reasoning.
- Four cubes are piled in a single stack to make a prism. Each cube has an edge length of \(\frac12\) inch. Sketch the prism, and find its volume in cubic inches.
-
Use cubes with an edge length of \(\frac12\) inch to build prisms with the lengths, widths, and heights shown in the table.
-
For each prism, record in the table how many \(\frac12\)-inch cubes can be packed into the prism and the volume of the prism.
prism
length (in)prism
width (in)prism
height (in)number of \(\frac12\)-inch
cubes in prismvolume of
prism (in3)\(\frac12\) \(\frac12\) \(\frac12\) 1 1 \(\frac12\) 2 1 \(\frac12\) 2 2 1 4 2 \(\frac32\) 5 4 2 5 4 \(2\frac12\) -
Examine the values in the table. What do you notice about the relationship between the edge lengths of each prism and its volume?
-
- What is the volume of a rectangular prism that is \(1\frac12\) inches by \(2\frac14\) inches by 4 inches? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A unit fraction has a 1 in the numerator.
-
These are unit fractions: \(\frac13, \frac{1}{100}, \frac11\).
-
These are not unit fractions: \(\frac29, \frac81, 2\frac15\).
-
Find three unit fractions whose sum is \(\frac12\). An example is: \( \frac18 + \frac18 + \frac14 = \frac12\) How many examples like this can you find?
-
Find a box whose surface area in square units equals its volume in cubic units. How many like this can you find?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may need a reminder to label volume in cubic units.
Activity Synthesis
Display a completed table for all to see. Give students a minute to check their responses. Invite a few students to share how they determined the volume of the prisms, and their observations about the relationships between the number of cubes (with \(\frac12\)-inch edge lengths) and the volume of prism in cubic inches. Highlight that the volume can be found by calculating the number of cubes and multiplying it by \(\frac 18\), because each small cube has a volume of \(\frac 18\) cubic inch.
If students do not notice a pattern in their table, ask them what they notice about the edge lengths of the prisms in the second, fourth, and sixth rows of the table and their corresponding volumes. Make sure they see that the volume of each prism can also be found by multiplying its side lengths. In other words, we can find the volume of a rectangular prism with fractional edge lengths the same way we find that of a prism with whole-number edge lengths.
Lesson Synthesis
Lesson Synthesis
In this lesson, we used division to solve for a missing base or height in a triangle. Review with students that we used a given area to find an unknown base or height.
- “How is finding an unknown base or height in a triangle different than finding an unknown side length in a rectangle?” (In a triangle, there are three factors at play.)
- “What multiplication equation can we write to help us find the height of a triangle that has a base of \(\frac 54\) cm and an area of 10 sq cm?” (\(\frac12 \boldcdot \frac54 \boldcdot h = 10\).)
- “How do we go about finding the unknown length?” (We can multiply the two known factors first. In this case, we can multiply \(\frac12 \boldcdot \frac54\) to get \(\frac 58\), and then divide 10 by \(\frac58\). Or we can divide by the factors one at a time—divide by \(\frac 12\) first, and then by \(\frac54\).)
What we know about fractions and operations can also help us find the volume of rectangular prisms when the edge lengths are not whole numbers.
- How can we use cubes with \(\frac12\)-inch edge lengths to find the volume of a prism that is \(\frac12\) inch by 2 inch by \(3\frac12\) inches? (We can think of the prism as being built of these cubes; the prism will have whole numbers of cubes for its edge lengths. In this case, they are 1, 4, and 7, so there are 28 cubes with \(\frac12\)-inch edge length. Each of these cubes is \(\frac18\) cubic inch because 8 of them fit in 1 cubic inch. The volume of the prism, in cubic inches, is then \(28 \boldcdot \frac18\), which is \(3 \frac 12\).)
- How else might we find the volume of a rectangular prism with fractional edge lengths? (We can multiply the three edge lengths in inches directly. \(\frac12 \boldcdot 2 \boldcdot \frac72 = \frac72 = 3\frac12\).)
14.4: Cool-down - Triangles and Cubes (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If a rectangular prism has edge lengths of 2 units, 3 units, and 5 units, we can think of it as 2 layers of unit cubes, with each layer having \((3 \boldcdot 5)\) unit cubes in it. So the volume, in cubic units, is: \(\displaystyle 2\boldcdot 3\boldcdot 5\)
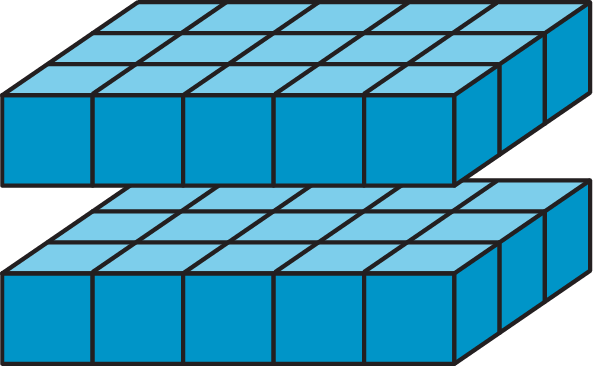
To find the volume of a rectangular prism with fractional edge lengths, we can think of it as being built of cubes that have a unit fraction for their edge length. For instance, if we build a prism that is \(\frac12\)-inch tall, \(\frac32\)-inch wide, and 4 inches long using cubes with a \(\frac12\)-inch edge length, we would have:
- A height of 1 cube, because \(1 \boldcdot \frac 12 = \frac12\).
- A width of 3 cubes, because \(3 \boldcdot \frac 12 = \frac32\).
- A length of 8 cubes, because \(8 \boldcdot \frac 12 = 4\).
The volume of the prism would be \(1 \boldcdot 3 \boldcdot 8\), or 24 cubic units. How do we find its volume in cubic inches? We know that each cube with a \(\frac12\)-inch edge length has a volume of \(\frac 18\) cubic inch, because \(\frac 12 \boldcdot \frac 12 \boldcdot \frac 12 = \frac18\). Since the prism is built using 24 of these cubes, its volume, in cubic inches, would then be \(24 \boldcdot \frac 18\), or 3 cubic inches.
The volume of the prism, in cubic inches, can also be found by multiplying the fractional edge lengths in inches: \(\frac 12 \boldcdot \frac 32 \boldcdot 4 = 3\)