Lesson 5
How Many Groups? (Part 2)
5.1: Reasoning with Fraction Strips (5 minutes)
Warm-up
In this warm-up, students continue to think of division in terms of equal-sized groups, using fraction strips as an additional tool for reasoning.
Notice how students transition from concrete questions (the first three) to symbolic ones (the last three). Framing division expressions as “how many of this fraction in that number?” may not yet be intuitive to students. They will further explore that connection in this lesson. For now, support them using whole-number examples (e.g., ask: “how do you interpret \(6 \div 2\)?”).
The divisors used here involve both unit fractions and non-unit fractions. The last question shows a fractional divisor that is not on the fraction strips. This encourages students to transfer the reasoning used with fraction strips to a new problem, or to use an additional strategy (e.g., by first writing an equivalent fraction).
As students work, notice those who are able to modify their reasoning effectively, even if the approach may not be efficient (e.g., adding a row of \(\frac {1}{10}\)s to the fraction strips). Ask them to share later.
Launch
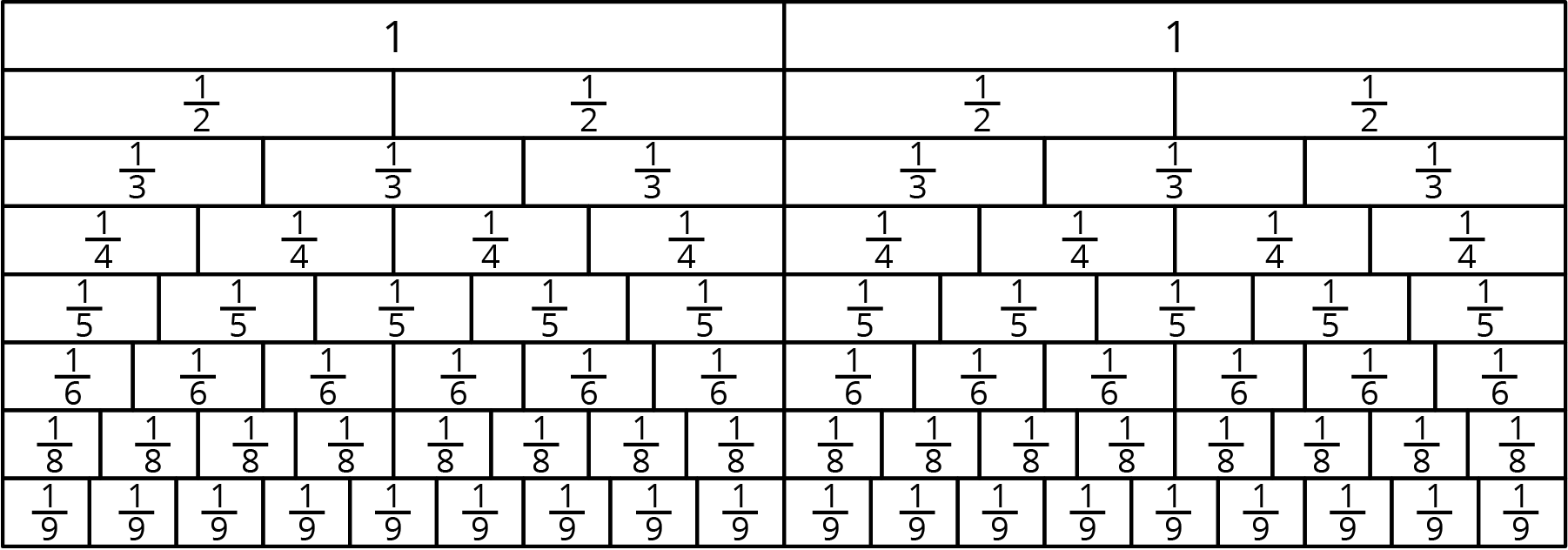
Student Facing
Write a fraction or whole number as an answer for each question. If you get stuck, use the fraction strips. Be prepared to share your reasoning.
- How many \(\frac 12\)s are in 2?
- How many \(\frac 15\)s are in 3?
- How many \(\frac {1}{8}\)s are in \(1\frac 14\)?
- \(1 \div \frac {2}{6} = {?}\)
- \(2 \div \frac 29 = {?}\)
- \(4 \div \frac {2}{10} = {?}\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Since the fraction strips do not show tenths, students might think that it is impossible to answer the last question. Ask them if they can think of another fraction that is equivalent to \(\frac{2}{10}\).
Activity Synthesis
For each of the first five questions, select a student to share their response and ask the class to indicate whether they agree or disagree.
Focus the discussion on two things: how students interpreted expressions such as \(1 \div \frac26\), and on how they reasoned about \(4 \div \frac {2}{10}\). Select a few students to share their reasoning.
For the last question, highlight strategies that are effective and efficient, such as using a unit fraction that is equivalent to \(\frac {2}{10}\), finding out how many groups of \(\frac15\) are in 1 and then multiplying it by 4, etc.
5.2: More Reasoning with Pattern Blocks (25 minutes)
Activity
This activity serves two purposes: to explicitly bridge “how many of this in that?” questions and division expressions, and to explore division situations in which the quotients are not whole numbers. (Students explored similar questions previously, but the quotients were whole numbers.)
Once again students move from reasoning concretely and visually to reasoning symbolically. They start by thinking about “how many rhombuses are in a trapezoid?” and then express that question as multiplication
(\(? \boldcdot \frac23 = 1\) or \(\frac 23 \boldcdot \,? = 1\)) and division (\(1 \div \frac23\)). Students think about how to deal with a remainder in such problems.
As students discuss in groups, listen for their explanations for the question “How many rhombuses are in a trapezoid?” Select a couple of students to share later—one person to elaborate on Diego's argument, and another to support Jada's argument.
Launch
Arrange students in groups of 3–4. Provide access to pattern blocks and geometry toolkits. Give students 10 minutes of quiet work time for the first three questions and a few minutes to discuss their responses and collaborate on the last question.
Classrooms with no access to pattern blocks or those using the digital materials can use the provided applet. Physical pattern blocks are still preferred, however.
Supports accessibility for: Conceptual processing; Memory
Student Facing
Use the pattern blocks in the applet to answer the questions. (If you need help aligning the pieces, you can turn on the grid.)
- If the trapezoid represents 1 whole, what do each of these other shapes represent? Be prepared to explain or show your reasoning.
-
1 triangle
-
1 rhombus
-
1 hexagon
-
-
Use pattern blocks to represent each multiplication equation. Use the trapezoid to represent 1 whole.
-
\(3 \boldcdot \frac 13=1\)
-
\(3 \boldcdot \frac 23=2\)
-
-
Diego and Jada were asked “How many rhombuses are in a trapezoid?”
- Diego says, “\(1\frac 13\). If I put 1 rhombus on a trapezoid, the leftover shape is a triangle, which is \(\frac 13\) of the trapezoid.”
- Jada says, “I think it’s \(1\frac12\). Since we want to find out ‘how many rhombuses,’ we should compare the leftover triangle to a rhombus. A triangle is \(\frac12\) of a rhombus.”
Do you agree with either of them? Explain or show your reasoning.
-
Select all the equations that can be used to answer the question: “How many rhombuses are in a trapezoid?”
-
\(\frac 23 \div {?} = 1\)
-
\({?} \boldcdot \frac 23 = 1\)
-
\(1 \div \frac 23 = {?}\)
-
\(1 \boldcdot \frac 23 = {?}\)
-
\({?} \div \frac 23 = 1\)
-
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 3–4. Provide access to pattern blocks and geometry toolkits. Give students 10 minutes of quiet work time for the first three questions and a few minutes to discuss their responses and collaborate on the last question.
Classrooms with no access to pattern blocks or those using the digital materials can use the provided applet. Physical pattern blocks are still preferred, however.
Supports accessibility for: Conceptual processing; Memory
Student Facing
Your teacher will give you pattern blocks. Use them to answer the questions.
-
If the trapezoid represents 1 whole, what do each of the other shapes represent? Be prepared to show or explain your reasoning.

-
Use pattern blocks to represent each multiplication equation. Use the trapezoid to represent 1 whole.
- \(3 \boldcdot \frac 13=1\)
- \(3 \boldcdot \frac 23=2\)
-
Diego and Jada were asked “How many rhombuses are in a trapezoid?”
- Diego says, “\(1\frac 13\). If I put 1 rhombus on a trapezoid, the leftover shape is a triangle, which is \(\frac 13\) of the trapezoid.”
- Jada says, “I think it’s \(1\frac12\). Since we want to find out ‘how many rhombuses,’ we should compare the leftover triangle to a rhombus. A triangle is \(\frac12\) of a rhombus.”
Do you agree with either of them? Explain or show your reasoning.
-
Select all the equations that can be used to answer the question: “How many rhombuses are in a trapezoid?”
- \(\frac 23 \div {?} = 1\)
- \(? \boldcdot \frac 23 = 1\)
- \(1 \div \frac 23 = {?}\)
- \(1 \boldcdot \frac 23 = {?}\)
- \({?} \div \frac23 = 1\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not notice that in this task, the trapezoid—not the hexagon—represents 1 whole. Encourage them to revisit the task statement to check.
Activity Synthesis
Focus the whole-class discussion on the last two questions, especially on how the visual representation helps us reason about Jada and Diego's points of view, and on the connections between the verbal and numerical representations of the situation.
Select two previously identified students to explain why Diego or Jada are correct. Display a visual representation of “how many rhombus are in a trapezoid?” for all to see (as shown here), or use the applet at https://ggbm.at/VmEqZvke for illustration.
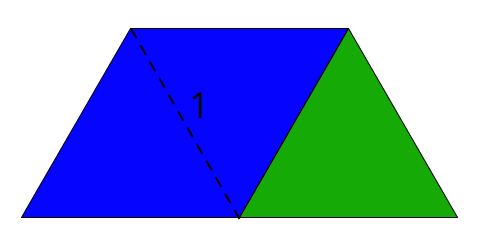
To highlight number of groups and size of one group in the problem, discuss questions such as:
- “This is a ‘how many groups of this in that?’ question. What makes 1 group, in this case?” (One rhombus.)
- “How do we know whether to compare the remainder to the rhombus or the trapezoid?” (Since a rhombus makes 1 group, we need to compare the remainder to the rhombus.)
If students struggle to compare the remainder to a rhombus, ask: “How many triangles are in a trapezoid?” and point out that the answer is “3 triangles.” Here, the answer to “how many rhombuses are in a trapezoid?” would be “(some number of) rhombuses.”
The fact that there are two 1 wholes to keep track of may be a source of confusion (the trapezoid represents the quantity 1 and the rhombus represents 1 group). Students will have opportunities to make clearer distinctions between the two 1 wholes in upcoming activities.
Design Principle(s): Support sense-making
5.3: Drawing Diagrams to Show Equal-sized Groups (20 minutes)
Optional activity
This activity gives students additional practice in using diagrams and equations to represent division situations involving whole numbers and fractions.
For each problem, many kinds of visual representations are possible, but creating a meaningful representation may be challenging nonetheless. Urge students to use the contexts to generate ideas for useful diagrams, and to start with a draft and modify it as needed. Students may also use the fraction strips in the warm-up as a starting point for drawing diagrams.
As students work and discuss, monitor for effective diagrams or those that can be generalized to different situations (e.g., rectangles, tape diagrams, and number lines). Assign one problem for each group to record on a visual display.
Launch
Arrange students in group of 3–4. Give students 8–10 minutes of quiet work time and a few minutes to share their responses with their group. Tell each group they will be asked to present their solution to one problem. Provide access to geometry toolkits and tools for creating a visual display.
During group discussion, ask students to exchange feedback on each other’s diagrams and to notice any that might be particularly effective, efficient, or easy to understand. Then, they should record the diagram and equations for their assigned problem on a visual display and be prepared to explain them.
Supports accessibility for: Visual-spatial processing
Student Facing
For each situation, draw a diagram for the relationship of the quantities to help you answer the question. Then write a multiplication equation or a division equation for the relationship. Be prepared to share your reasoning.
- The distance around a park is \(\frac32\) miles. Noah rode his bicycle around the park for a total of 3 miles. How many times around the park did he ride?
- You need \(\frac34\) yard of ribbon for one gift box. You have 3 yards of ribbon. How many gift boxes do you have ribbon for?
- The water hose fills a bucket at \(\frac13\) gallon per minute. How many minutes does it take to fill a 2-gallon bucket?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may mistake the divisor and the dividend in the problems. Ask students to discuss (in their groups) the number or quantity being divided, and the reasonableness of the different ways of setting up each problem given the context. Representing the situations with objects may also help.
Activity Synthesis
Invite each group to present the solution on their visual display. Ask the rest of the class to think about two things: whether the equations make sense, and how the presented diagram shows the number of groups, the size of each group, and a total amount. Doing so will help students see the structure of the problems in the equations and diagrams.
Make sure students understand how each situation can be expressed by multiplication and division equations. Students should recognize that a question such as “how many batches are in 4 cups if each batch requires \(\frac23\) cups?” can be written as both \(? \boldcdot \frac 23 = 4\) and \(4 \div \frac 23 = \,?\). With repeated reasoning, they see that a division expression such as \(5 \div \frac 38\) can be interpreted as “how many \(\frac38\)s are in 5?”
Design Principle(s): Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
In this lesson, we answered questions such as “how many of this fraction in that number?” or “how many groups of this in that?” We used pattern blocks, fraction strips, diagrams, and equations to help us make sense of those situations. The answers to those questions, we noticed, may not be whole numbers.
-
“We can think of the question ‘how many \(\frac34\) are in 2?’ in terms of equal-size groups. What do the \(\frac34\) and 2 represent? What are we looking for?” (\(\frac34\) is the size of each group. The 2 is the total amount. We are looking for the number of groups.)
-
“What multiplication equation can we write for this situation?” \(({?} \boldcdot \frac34 = 2)\)
-
“What division equation can we write?” (\(2 \div \frac34 = {?}\))
-
“We can draw a diagram and count how many groups of \(\frac34\) there are in 2. How many whole groups of \(\frac34\) are there?” (2 whole groups.)
-
“How do we deal with a remainder that is less than one whole group?” (We can compare the size of the remainder with the amount in one group. In \(2 \div \frac34 = {?}\), each group is \(\frac34\), and the remainder is \(\frac 24\), which is \(\frac23\) of one group.)
5.4: Cool-down - Bags of Tangerines (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Suppose one batch of cookies requires \(\frac23\) cup flour. How many batches can be made with 4 cups of flour?
We can think of the question as being: “How many \(\frac23\) are in 4?” and represent it using multiplication and division equations.
\(\displaystyle {?} \boldcdot \frac23 = 4\) \(\displaystyle 4\div \frac23 = {?}\)
Let’s use pattern blocks to visualize the situation and say that a hexagon is 1 whole.
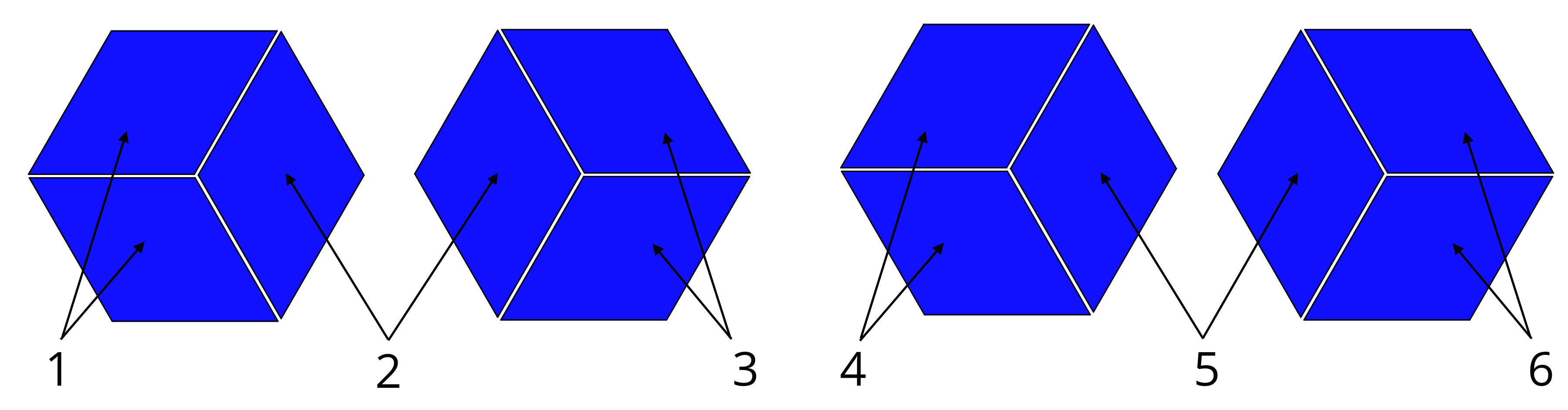
Since 3 rhombuses make a hexagon, 1 rhombus represents \(\frac13\) and 2 rhombuses represent \(\frac 23\). We can see that 6 pairs of rhombuses make 4 hexagons, so there are 6 groups of \(\frac 23\) in 4.
Other kinds of diagrams can also help us reason about equal-sized groups involving fractions. This example shows how we might reason about the same question from above: “How many \(\frac 23\)-cups are in 4 cups?”
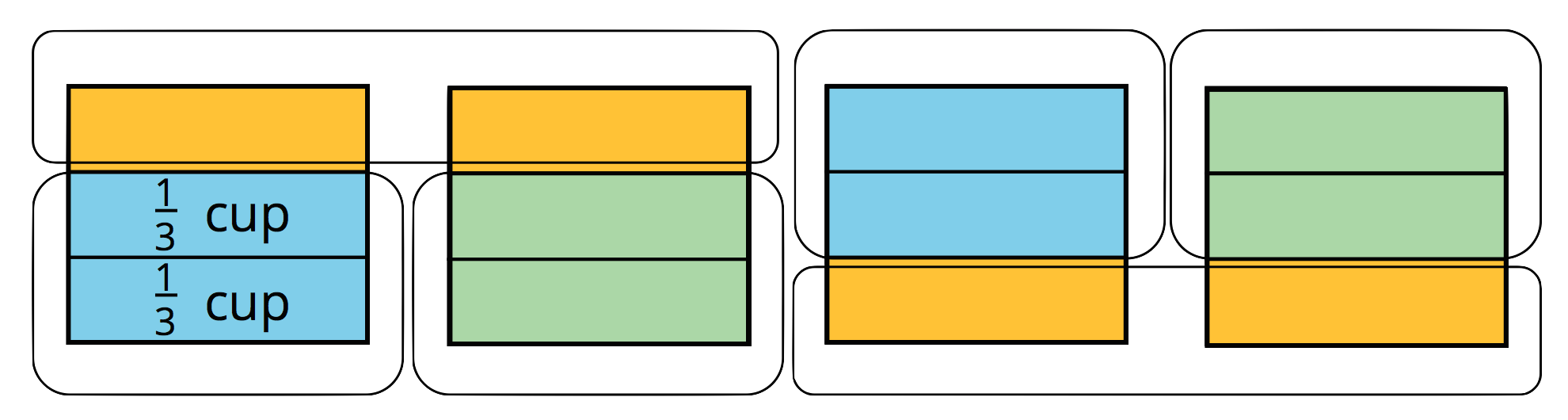
We can see each “cup” partitioned into thirds, and that there are 6 groups of \(\frac23\)-cup in 4 cups. In both diagrams, we see that the unknown value (or the “?” in the equations) is 6. So we can now write:
\(\displaystyle 6 \boldcdot \frac23 = 4\) \(\displaystyle 4\div \frac23 = 6\)