Lesson 10
Dividing by Unit and Non-Unit Fractions
10.1: Dividing by a Whole Number (10 minutes)
Warm-up
In this warm-up, students use tape diagrams to revisit the idea that dividing by a whole number is equivalent to multiplying by a unit fraction. Though this is a review of a grade 5 expectation, connecting the division problems to diagrams allows students to see the equivalence in the related division and multiplication problems. It also prepares students to extend the reasoning and representations used here to division by non-unit fractions later.
Launch
Arrange students in groups of 2. Ask one person in each group to draw diagrams and answer the questions for Partner A, and the other to take on the questions for Partner B. Give students a few minutes of quiet time to complete the first two questions, and then ask them to collaborate on the last two.
Student Facing
Work with a partner. One person solves the problems labeled “Partner A” and the other person solves those labeled “Partner B.” Write an equation for each question. If you get stuck, consider drawing a diagram.
-
Partner A:
How many 3s are in 12?
Division equation:

How many 4s are in 12?
Division equation:

How many 6s are in 12?
Division equation:

Partner B:
What is 12 groups of \(\frac 13\)?
Multiplication equation:

What is 12 groups of \(\frac 14\)?
Multiplication equation:

What is 12 groups of \(\frac 16\)?
Multiplication equation:

-
What do you notice about the diagrams and equations? Discuss with your partner.
-
Complete this sentence based on what you noticed:
Dividing by a whole number \(a\) produces the same result as multiplying by ________.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite a couple of students to share their observations about their group's diagrams and answers. Students should notice that the answers for the three division problems match those for the multiplication ones, even though the questions were not the same and their diagrams show groups of different sizes. Ask a few students to share their response to the last question.
Consider displaying the following image to reinforce the idea that dividing by a whole number has the same effect as multiplying by the reciprocal of that number.

10.2: Dividing by Unit Fractions (15 minutes)
Activity
In this activity, students use tape diagrams and the meanings of division to divide a number by unit fractions. They do this as a first step toward generalizing the reasoning for dividing any two fractions. By reasoning repeatedly and noticing a pattern (MP8), students arrive at the conclusion that \(a \div \frac1b\) is equivalent to \(a \boldcdot b\).
Later, students put together those results to see that dividing by a fraction \(\frac{c}{d}\) is equivalent to dividing by \(c\) and multiplying by \(d\).
As students work, notice those who are able to transfer the reasoning in the first two problems to subsequent problems without the help of diagrams. Select several students to share later.
Launch
Arrange students in groups of 2. Give students 5–6 minutes of quiet work time and then time to share their work with a partner. Provide access to colored pencils. Some students may find it helpful to identify whole groups and partial groups on a tape diagram by coloring.
For classes using the digital materials, an applet from an earlier lesson can also be used to represent the division problems here,
Student Facing
To find the value of \(6 \div \frac 12\), Elena thought, “How many \(\frac 12\)s are in 6?” and then she drew this tape diagram. It shows 6 ones, with each one partitioned into 2 equal pieces.
\(6 \div \frac 12\)
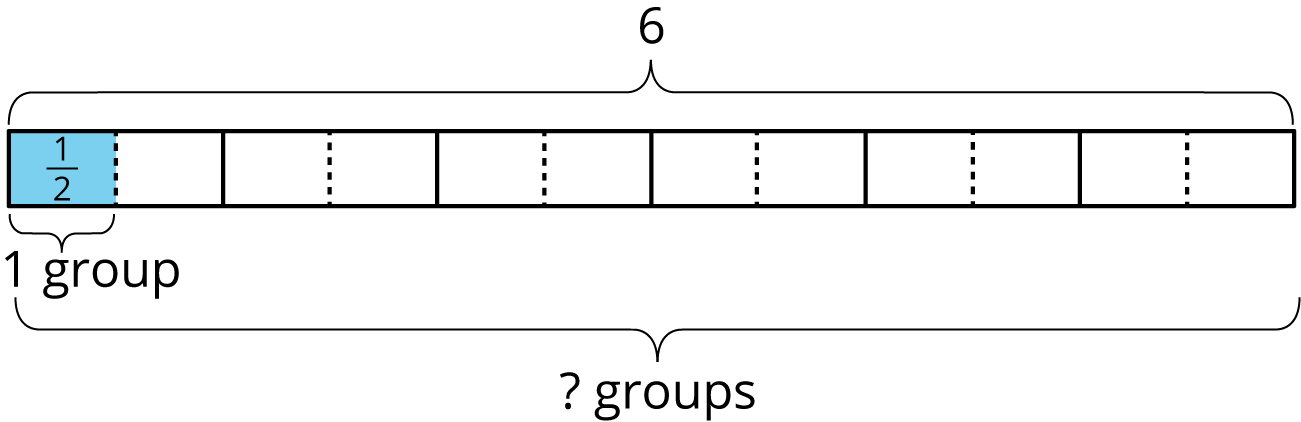
- For each division expression, complete the diagram using the same method as Elena. Then, find the value of the expression.
-
\(6 \div \frac 13\)
Value of the expression: ____________
-
\(6 \div \frac 14\)
Value of the expression: ____________
-
\(6 \div \frac 16\)
Value of the expression: ____________
-
-
Examine the expressions and answers more closely. Look for a pattern. How could you find how many halves, thirds, fourths, or sixths were in 6 without counting all of them? Explain your reasoning.
-
Use the pattern you noticed to find the values of these expressions. If you get stuck, consider drawing a diagram.
- \(6 \div \frac 18\)
- \(6 \div \frac {1}{10}\)
- \(6 \div \frac {1}{25}\)
- \(6 \div \frac {1}{b}\)
-
Find the value of each expression.
- \(8 \div \frac 14\)
- \(12 \div \frac 15\)
- \(a \div \frac 12\)
- \(a \div \frac {1}{b}\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
For some students, the structure in the division may still not be apparent by the time they get to problems such as \(6 \div \frac{1}{25}\), and they may try to partition a section in a tape diagram into 25 parts. Ask them to study the diagrams as well as the answers to the previous questions carefully and to look for a pattern.
Activity Synthesis
Select previously identified students to share their responses to the questions \(6 \div \frac {1}{b}\) and \(a \div \frac {1}{b}\). To highlight the connections between the diagram, division by a unit fraction, and multiplication by the reciprocal of the fraction ask students:
- “How is the division by a unit fraction depicted in the diagrams?” (The tape diagram is broken into equal parts. The unit fraction is the size of each part.)
- “Where in the diagrams do we see the multiplication?” (The multiplication shows the number of parts in each 1 whole.)
- “How are the two—the division by a unit fraction and the multiplication—related?” (When we divide a number by a unit fraction \(\frac1b\), we end up with \(b\) times as many parts, so dividing by \(\frac1b\) is the same as multiplying by \(b\).)
If not already articulated by students, clarify that dividing a number by a unit fraction has the same result as multiplying by its reciprocal.
Discuss the usefulness and limits of diagrams. Ask:
- “How do we find the value of \(1,\!000 \div \frac 19\) or \(2 \div \frac{1}{250}\) using a diagram?” (By dividing each 1 whole into 9 parts or 250 parts)
- “Would you use diagrams to find these quotients? Why or why not?” (No, it is not practical.)
- “When working on the task, did you stop partitioning the tape diagrams at some point? If so, why?”
- “Why do we use diagrams? When can they be helpful?” (Diagrams can show us the structure or relationships between numbers and help us see the general process.)
If not mentioned by students, point out that for larger numbers, or smaller fractions, drawing a full diagram becomes increasingly cumbersome. Noticing the structure that is visible in the diagrams for easier cases allows us to use it for more difficult ones.
Design Principle(s): Support sense-making
10.3: Dividing by Non-unit Fractions (15 minutes)
Activity
Here students continue to use tape diagrams to reason about division and extend their observations about unit fractions to non-unit fractions. Specifically, they explore how to represent the numerator of the fraction in the tape diagram and study its effect on the quotient. Students generalize their observations as operational steps and then as expressions, which they then use to solve other division problems.
As students work, notice those who effectively show the divisor on their diagrams, i.e., the multiplication by the denominator and division by the numerator, as well as those who could explain why the steps make sense.
Launch
Keep students in groups of 2. Give students 5–7 minutes of quiet work time and then time to share their responses with their partner. Provide continued access to colored pencils.
Student Facing
- To find the value of \(6 \div \frac 23\), Elena started by drawing a diagram the same way she did for \(6 \div \frac 13\).
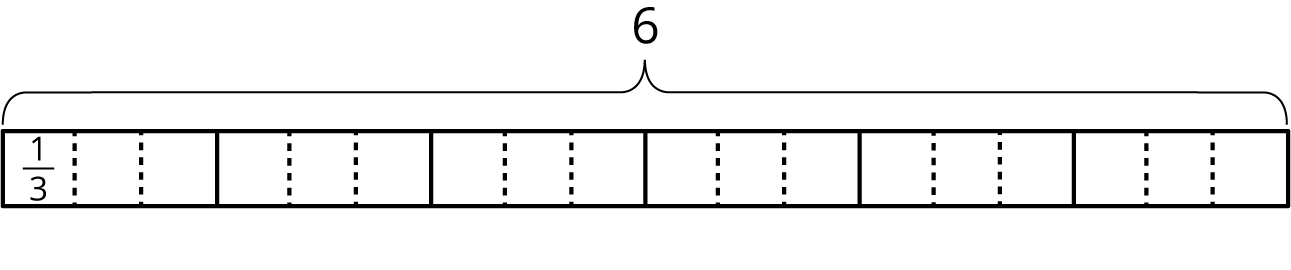
- Complete the diagram to show how many \(\frac 23\)s are in 6.
- Elena says, “To find \(6 \div \frac23\), I can just take the value of \(6 \div \frac13\) and then either multiply it by \(\frac 12\) or divide it by 2.” Do you agree with her? Explain your reasoning.
-
For each division expression, complete the diagram using the same method as Elena. Then, find the value of the expression. Think about how you could find that value without counting all the pieces in your diagram.
-
\(6 \div \frac 34\)
Value of the expression:___________
-
\(6 \div \frac 43\)
Value of the expression:___________
-
\(6 \div \frac 46\)
Value of the expression:___________
-
-
Elena examined her diagrams and noticed that she always took the same two steps to show division by a fraction on a tape diagram. She said:
“My first step was to divide each 1 whole into as many parts as the number in the denominator. So if the expression is \(6 \div \frac 34\), I would break each 1 whole into 4 parts. Now I have 4 times as many parts.
My second step was to put a certain number of those parts into one group, and that number is the numerator of the divisor. So if the fraction is \(\frac34\), I would put 3 of the \(\frac 14\)s into one group. Then I could tell how many \(\frac 34\)s are in 6.”
Which expression represents how many \(\frac 34\)s Elena would have after these two steps? Be prepared to explain your reasoning.
- \(6 \div 4 \boldcdot 3\)
- \(6 \div 4 \div 3\)
- \(6 \boldcdot 4 \div 3\)
- \(6 \boldcdot 4 \boldcdot 3\)
-
Use the pattern Elena noticed to find the values of these expressions. If you get stuck, consider drawing a diagram.
- \(6 \div \frac27\)
- \(6\div\frac{3}{10}\)
- \(6 \div \frac {6}{25}\)
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Find the missing value.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may read the phrase “partition 1 section into 4 parts” in Elena's reasoning and focus on the value of each small part \(\left(\frac 14\right)\) instead on how many parts are now shown. Similarly, they may take “making of 3 of these parts into one piece” to imply multiplying the \(\frac14\) by 3, instead of looking at how it changes the number of pieces. Explain that Elena's diagram& suggests that she interpreted \(6 \div \frac34\) as “how many \(\frac34\)s are in 6?” which tells us that we are looking for the number of groups, rather than the value of each part in the diagram.
Activity Synthesis
Select a few students to share their diagrams and explanations about why Elena's reasoning and method work. Display the following tape diagram for \(6 \div \frac 34\), if needed. Ask students to point out where in the diagram the two steps are visible.
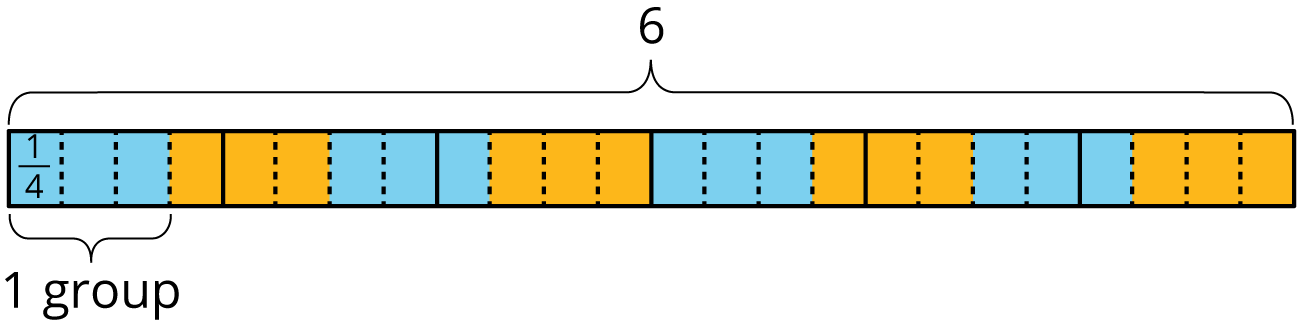
To involve more students in the conversation, consider asking questions such as:
- “Who can restate ___'s reasoning in different words?”
- “Did anyone think about the division the same way but would explain it differently?”
- “Does anyone want to add an observation to the way ____ reasoned about the division?”
- “Do you agree or disagree? Why?”
Highlight that dividing a number \(c\) by a fraction \(\frac {a}{b}\) has the same result as multiplying by \(b\), then dividing by \(a\) (or multiplying by \(\frac {1}{a}\)).
Design Principle(s): Support sense-making, Cultivate conversation
Lesson Synthesis
Lesson Synthesis
In this lesson, we reasoned about fraction division using tape diagrams. We traced the steps in our reasoning and analyzed the outcomes.
-
“What did we notice about the result of dividing a number by a unit fraction? Can you explain with an example?” (It has the same outcome as multiplying by the denominator of the fraction.)
-
“What observations did we make when dividing a number by a non-unit fraction? Can you explain with an example?” (It has the same outcome as multiplying by the denominator of the fraction and dividing by the numerator, and dividing by the numerator is the same as multiplying by its reciprocal.)
-
“Suppose we are finding \(5 \div \frac{7}{25}\). How might these observations help us find this quotient?” (We can multiply 5 by 25 and then divide by 7, instead of drawing a diagram and breaking each 1 into 25 parts, and so on.)
Emphasize that recognizing the patterns in how we reason about division of simpler fractions can help us divide other fractions more efficiently. Instead of drawing and reasoning with diagrams, which could be time consuming, we can follow the same series of steps to find quotients.
10.4: Cool-down - Dividing by $\frac 13$ and $\frac 35$ (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
To answer the question “How many \(\frac 13\)s are in 4?” or “What is \(4 \div \frac 13\)?”, we can reason that there are 3 thirds in 1, so there are \((4\boldcdot 3)\) thirds in 4.
In other words, dividing 4 by \(\frac13\) has the same result as multiplying 4 by 3.
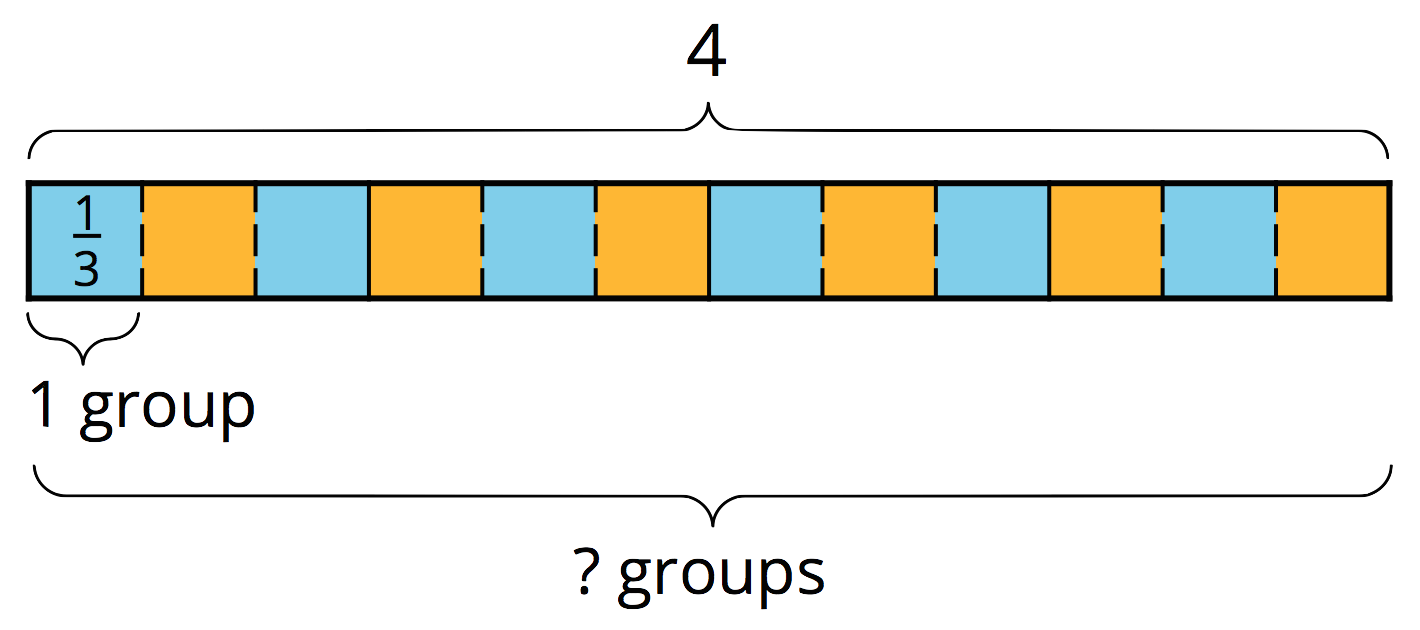
\(\displaystyle 4\div \frac13 = 4 \boldcdot 3\)
In general, dividing a number by a unit fraction \(\frac{1}{b}\) is the same as multiplying the number by \(b\), which is the reciprocal of \(\frac{1}{b}\).
How can we reason about \(4 \div \frac23\)?
We already know that there are \((4\boldcdot 3)\) or 12 groups of \(\frac 13\)s in 4. To find how many \(\frac23\)s are in 4, we need to put together every 2 of the \(\frac13\)s into a group. Doing this results in half as many groups, which is 6 groups. In other words:
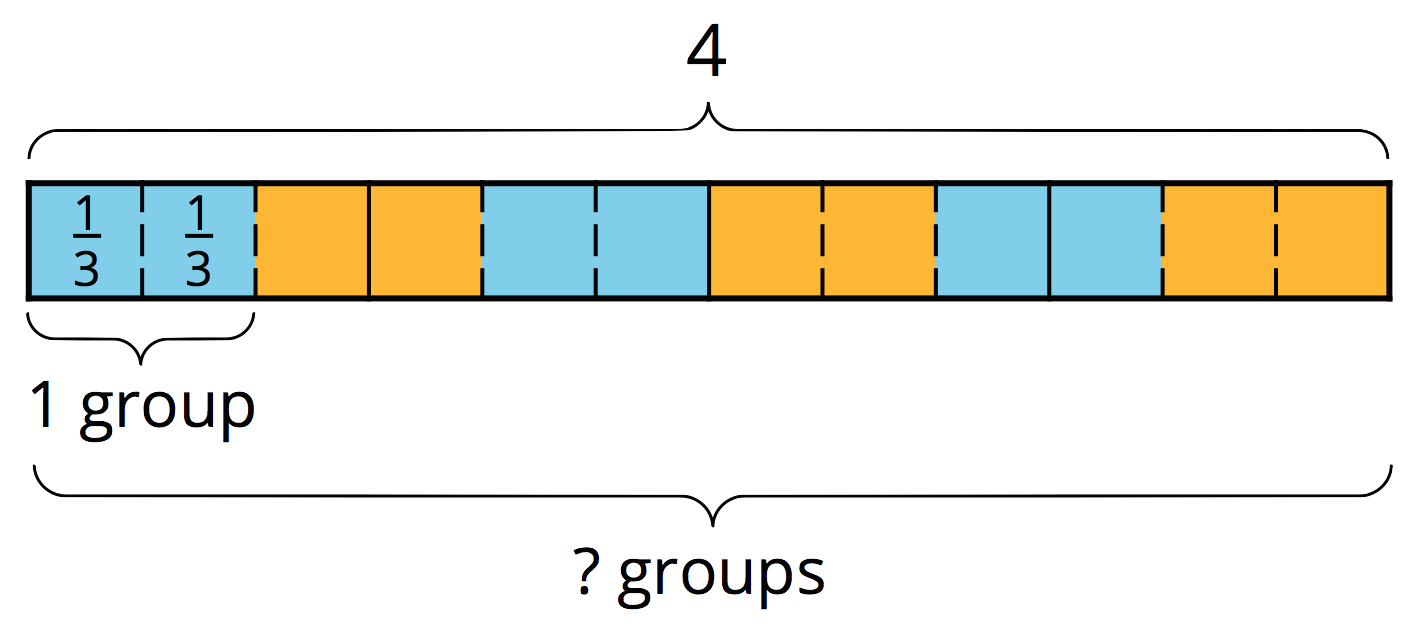
\(\displaystyle 4 \div \frac23 = (4 \boldcdot 3) \div 2\)
or
\(\displaystyle 4 \div \frac23 = (4 \boldcdot 3) \boldcdot \frac 12\)
In general, dividing a number by \(\frac{a}{b}\), is the same as multiplying the number by \(b\) and then dividing by \(a\), or multiplying the number by \(b\) and then by \(\frac{1}{a}\).