Lesson 3
Interpreting Division Situations
3.1: Dot Image: Properties of Multiplication (5 minutes)
Warm-up
In this warm-up, students determine the number of dots in an image without counting and explain how they arrived at that answer. The goal is to prompt them to visualize and articulate different ways to decompose the dots, using what they know about arrays, multiplication, and area to arrive at the total number. To discourage counting and encourage students to focus on the structure of the dots, the image will be flashed and hidden a couple of times, rather than displayed the entire time.
Launch
Tell students to keep their materials closed. Explain that you will show an image that contains dots for 3 seconds. Their job is to determine how many dots there are and explain how they saw them.
Display the image for 3 seconds and then hide it. Do this twice. Give students up to 1 minute of quiet think time after each flash. Encourage students who have one way of seeing the dots to think about another way while they wait.
Supports accessibility for: Memory; Organization
Student Facing

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select a couple of students to share the number of dots they saw. To focus students' reasoning on the structure of the dots, ask how they saw them, instead of how they found them. Record and display student explanations for all to see. Consider re-displaying the image to support students in their explanation.
To involve more students in the conversation, consider asking:
- Who can restate the way ___ saw the dots in different words?
- Did anyone see the dots the same way but would explain it differently?
- Does anyone want to add an observation to the way ____ saw the dots?
- Who saw the dots differently?
- Do you agree or disagree? Why?
3.2: Homemade Jams (20 minutes)
Activity
This activity allows students to draw diagrams and write equations to represent simple division situations. Some students may draw concrete diagrams; others may draw abstract ones. Any diagrammatic representation is fine as long as it enables students to make sense of the relationship between the number of groups, the size of a group, and a total amount.
The last question is likely more challenging to represent with a diagram. Because the question asks for the number of jars, and because the amount per jar is a fraction, students will not initially know how many jars to draw (unless they know what \(6\frac34 \div \frac34\) is). Suggest that they start with an estimate, and as they reason about the problem, add jars to (or remove jars from) their diagram as needed.
As students work, monitor for the range of diagrams that students create. Select a few students whose work represent the range of diagrams to share later.
Students in digital classrooms can use an applet to make sense of the problems, but it is still preferable that they create their own diagrams.
Launch
Arrange students in groups of 2. Tell the class that you will read the three story problems, and ask them to be prepared to share at least one thing they notice and one thing they wonder. After reading, give them a minute to share their observation and question with their partner.
Clarify that their job is to draw a diagram and write a multiplication equation to express the relationship in each story and then answer the question. Give students 7–8 minutes of quiet work time, followed by 2–3 minutes to share their work with their partner.
If the applet is used to complete the activity or for class discussion, note that the toolbar includes colored rectangles that represent fractional parts. Encourage students to drop the fractional parts in the work space on the left of the window, and then use the Move tool (the arrow) to drag them into the jars. The blocks do snap, but the grid is very fine so this may be challenging for some students. Troubleshooting tip: if two blocks get stuck together, delete them. Try not to overlap blocks when adding them to the work space.
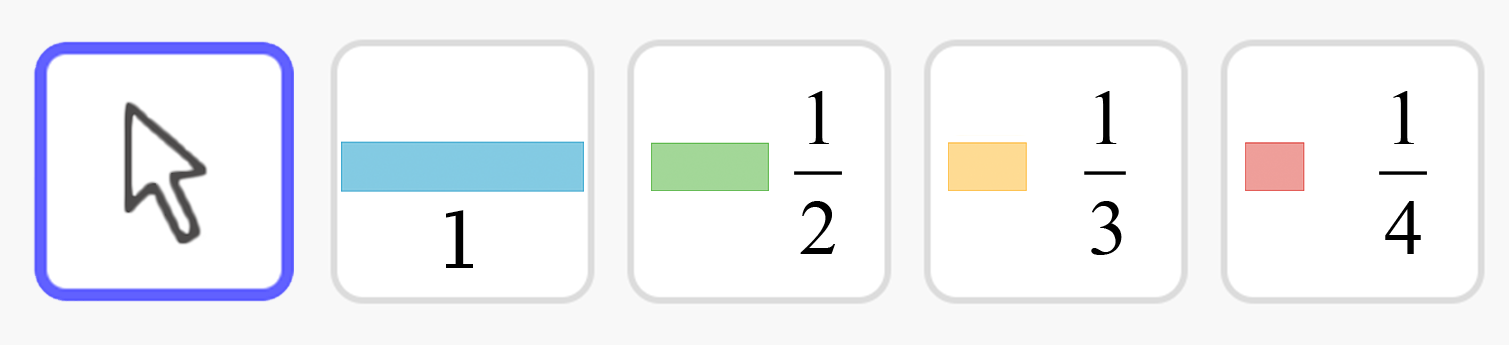
Student Facing
Draw a diagram and write a multiplication equation to represent each situation. Then answer the question.
- Mai had 4 jars. In each jar, she put \(2\frac14\) cups of homemade blueberry jam. Altogether, how many cups of jam are in the jars?
- Priya filled 5 jars, using a total of \(7\frac12\) cups of strawberry jam. How many cups of jam are in each jar?
- Han had some jars. He put \(\frac34\) cup of grape jam in each jar, using a total of \(6\frac34\) cups. How many jars did he fill?
Here is an applet to use if you choose to.
The toolbar includes buttons that represent 1 whole and fractional parts, as shown here. Click a button to choose a quantity, and then click in the work space of the applet window to drop it. When you're done choosing pieces, use the Move tool (the arrow) to drag them into the jars. You can always go back and get more pieces, or delete them with the Trash Can tool.
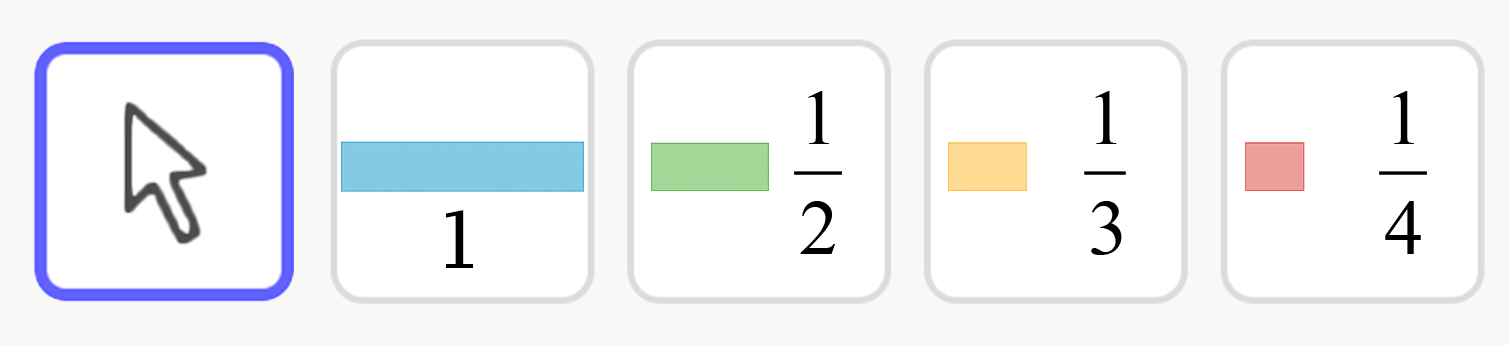
The jars in this applet are shown as stacked to make it easier to combine the jam and find out how much you have.
Here are the questions again.
- Mai had 4 jars. In each jar, she put \(2\frac14\) cups of homemade blueberry jam. Altogether, how many cups of jam are in the jars?
- Priya filled 5 jars, using a total of \(7\frac12\) cups of strawberry jam. How many cups of jam are in each jar?
- Han had some jars. He put \(\frac34\) cup of grape jam in each jar, using a total of \(6\frac34\) cups. How many jars did he fill?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Tell the class that you will read the three story problems, and ask them to be prepared to share at least one thing they notice and one thing they wonder. After reading, give them a minute to share their observation and question with their partner.
Clarify that their job is to draw a diagram and write a multiplication equation to express the relationship in each story and then answer the question. Give students 7–8 minutes of quiet work time, followed by 2–3 minutes to share their work with their partner.
If the applet is used to complete the activity or for class discussion, note that the toolbar includes colored rectangles that represent fractional parts. Encourage students to drop the fractional parts in the work space on the left of the window, and then use the Move tool (the arrow) to drag them into the jars. The blocks do snap, but the grid is very fine so this may be challenging for some students. Troubleshooting tip: if two blocks get stuck together, delete them. Try not to overlap blocks when adding them to the work space.

Student Facing
Draw a diagram, and write a multiplication equation to represent each situation. Then answer the question.
- Mai had 4 jars. In each jar, she put \(2\frac14\) cups of homemade blueberry jam. Altogether, how many cups of jam are in the jars?
- Priya filled 5 jars, using a total of \(7\frac12\) cups of strawberry jam. How many cups of jam are in each jar?
- Han had some jars. He put \(\frac34\) cup of grape jam in each jar, using a total of \(6\frac34\) cups. How many jars did he fill?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select previously identified students to share their diagrams, sequenced from the more concrete (e.g., pictures of jars and cups) to the more abstract (e.g, rectangles, tape diagrams). Display the diagrams and equations for all to see. Ask them how they used the diagrams to answer the questions (if at all).
If tape diagrams such as the ones here are not already shown and explained by a student, display them for all to see. Help students make sense of the diagrams and connecting them to multiplication and division by discussing questions such as these:
- “In each diagram, what does the ‘?’ represent?” (The unknown amount)
- “What does the length of the entire tape represent?” (The total amount, which is sometimes known.)
- “What does each rectangular part represent?” (One jar)
- “What does the number in each rectangle represent?” (The amount in each jar)
- “How do the three parts of each multiplication equation relate to the diagram?” (The first factor refers to the number of rectangles. The second factor refers to the amount in each rectangle. The product is the total amount.)
- “The last diagram doesn't represent all the jars and shows a question mark in the middle of the tape. Why might that be?” (The diagram shows an unknown number of jar, which was the question to be answered.)
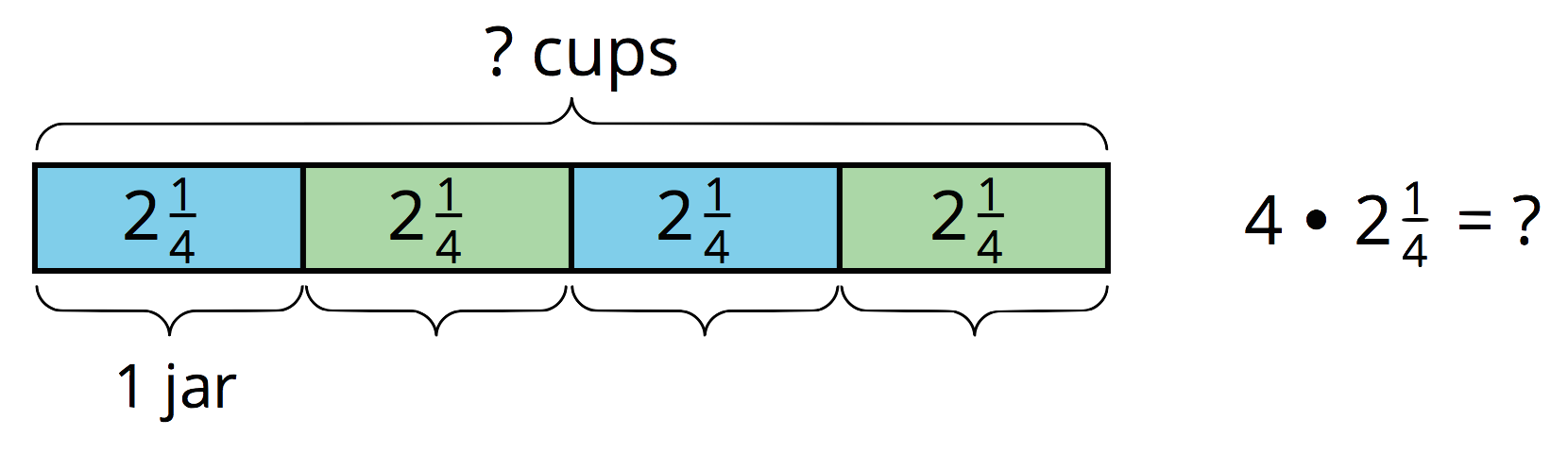
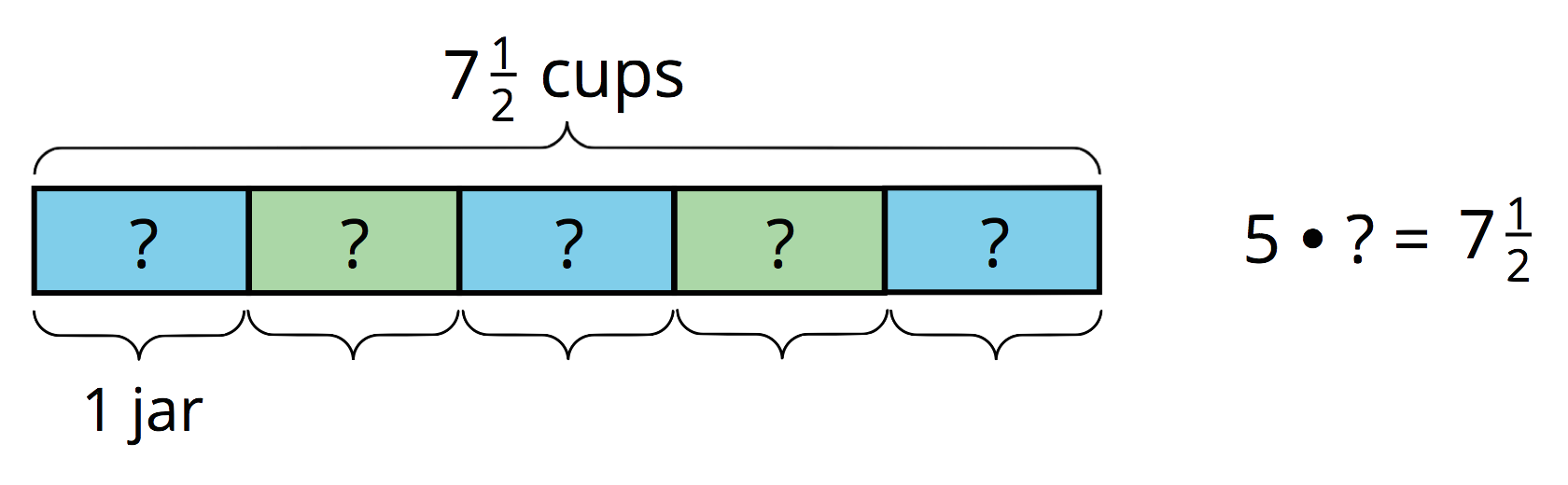
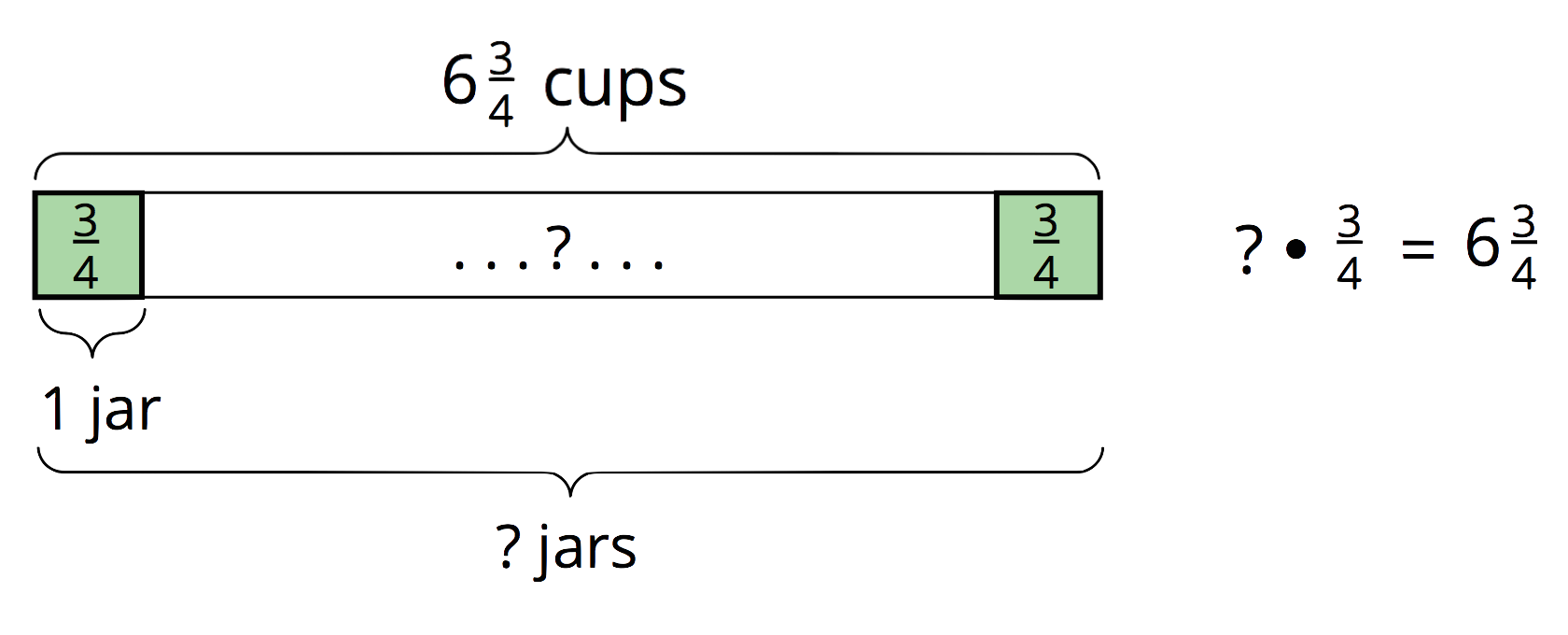
Highlight that the last two situations can be described with division: \(7\frac12 \div 5\) and \(6\frac34 \div \frac34\).
Design Principle(s): Support sense-making
3.3: Making Granola (15 minutes)
Activity
In this activity, students continue to investigate division problems in context, think of them in terms of equal-size groups, and represent them using diagrams and equations.
As students work, monitor the different diagrams and interpretations for each problem. Select students whose diagrams are especially clear in showing the meanings of division to share later.
Both division problems result in quotients that are not whole numbers. As students work, encourage them to use their multiplication equations to check the answers to the division problems.
Launch
Keep students in the same groups. Some students may not be familiar with granola and oats, so show or explain what they are.
Give students 7–8 minutes of quiet work time, and 2–3 minutes to discuss their responses with a partner. During partner discussion, ask them to compare their equations and diagrams in the first question, and their interpretations of division in the second question.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
-
Consider the problem: To make 1 batch of granola, Kiran needs 26 ounces of oats. The only measuring tool he has is a 4-ounce scoop. How many scoops will it take to measure 26 ounces of oats?
- Will the answer be more than 1 or less than 1?
- Write a multiplication equation and a division equation that represent this situation. Use “?” to represent the unknown quantity.
- Find the unknown quantity. If you get stuck, consider drawing a diagram.
-
The recipe calls for 14 ounces of mixed nuts. To get that amount, Kiran uses 4 bags of mixed nuts.
- Write a mathematical question that might be asked about this situation.
- What might the equation \(14 \div 4 =\, {?}\) represent in Kiran’s situation?
- Find the quotient. Show your reasoning. If you get stuck, consider drawing a diagram.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may round their answers to the nearest whole number rather than including the fractions of a scoop or a batch. Ask students to consider if it is possible to have a part of a scoop, a part of a batch, or a part of a unit of weight. Encourage them to think about how to show a part of a whole unit on a diagram.
Activity Synthesis
The aim of the discussion is to solidify students' understanding of the two interpretations of division (“how many groups?” and “how much in a group?”). Ask students who drew effective diagrams to display and explain them. For each interpretation, write a multiplication equation and discuss what each factor represents in the context (e.g., the number of batches, scoops, or bags, vs. how much is in each batch, scoop, or bag).
If no students drew tape diagrams to represent the situations, show the following. Reiterate that each rectangle represents one group (one scoop or 1 bag), the number inside represents the amount in one group, and the number of rectangles tells us how many groups there are.
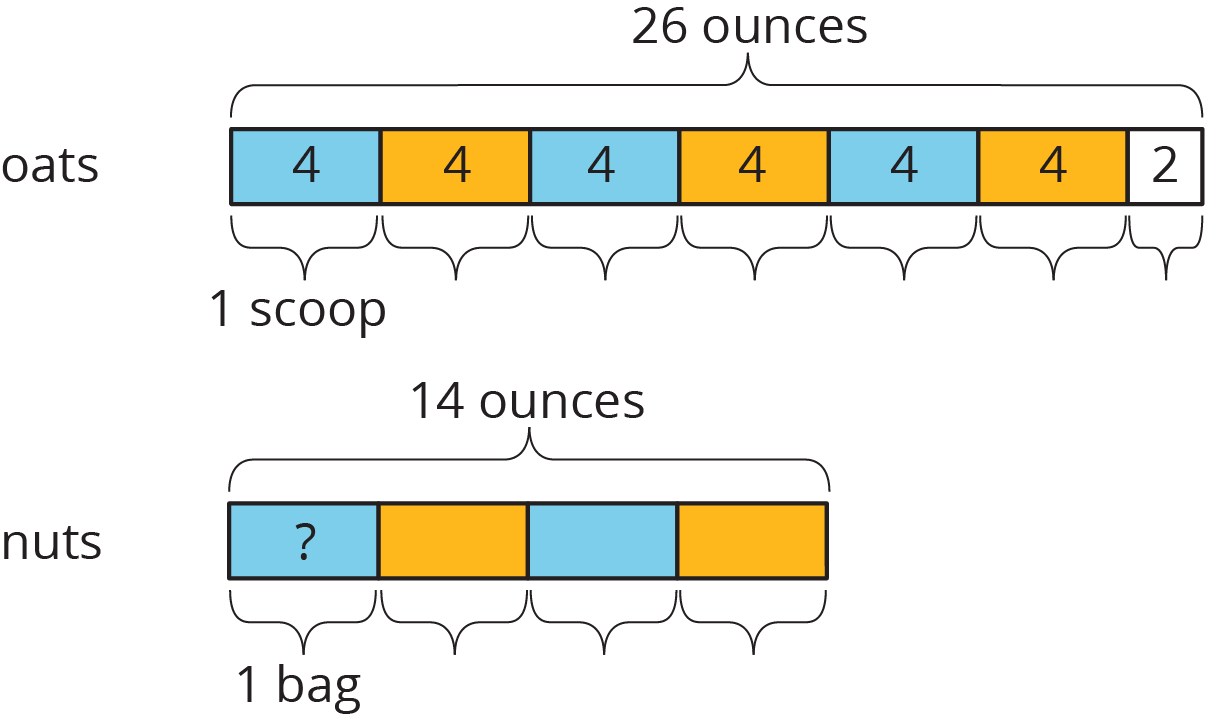
Lesson Synthesis
Lesson Synthesis
In this lesson, we solved problems that involved multiplication and division. Reiterate to students that in division situations that involve equal-size groups, we are not always looking for the same unknown. There are typically three pieces of information involved: the number of groups, the size of each group, and the total amount. Knowing what information we have and what is missing can help us answer questions.
Present a few more story problems. Ask students: "What information is unknown in each situation?"
-
Flour is sold in 3-pound bags. How many pounds are in 7 bags? (The total amount is unknown.)
-
Five tickets to a play cost \$38. What does each ticket cost if they all cost the same? (The amount for one person is unknown.)
-
One quart is equal to 32 ounces. How many quarts are in 128 ounces? (The number of groups is unknown.)
For each problem, discuss: “What multiplication equation can we write? What diagram can we draw to represent the quantities?”
3.4: Cool-down - Rice and Beans (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If a situation involves equal-sized groups, it is helpful to make sense of it in terms of the number of groups, the size of each group, and the total amount. Here are three examples to help us better understand such situations.
- Suppose we have 3 bottles with \(6\frac12\) ounces of water in each, and the total amount of water is not given. Here we have 3 groups, \(6\frac12\) ounces in each group, and an unknown total, as shown in this diagram:
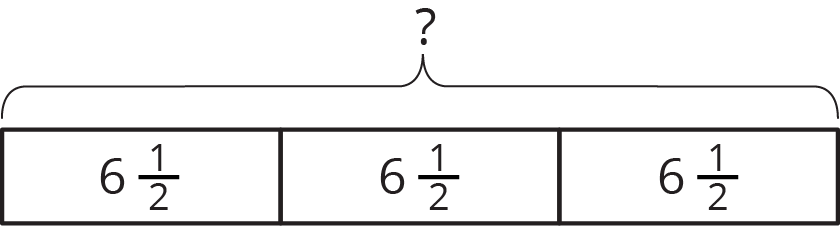
We can express this situation as a multiplication problem. The unknown is the product, so we can simply multiply the 2 known numbers to find it. \(\displaystyle 3 \boldcdot 6\frac12 = {?}\)
- Next, suppose we have 20 ounces of water to fill 6 equal-sized bottles, and the amount in each bottle is not given. Here we have 6 groups, an unknown amount in each, and a total of 20. We can represent it like this:

This situation can also be expressed using multiplication, but the unknown is a factor, rather than the product: \(\displaystyle 6\, \boldcdot {?} = 20\)
To find the unknown, we cannot simply multiply, but we can think of it as a division problem: \(\displaystyle 20 \div 6 = \,?\)
- Now, suppose we have 40 ounces of water to pour into bottles, 12 ounces in each bottle, but the number of bottles is not given. Here we have an unknown number of groups, 12 in each group, and a total of 40.
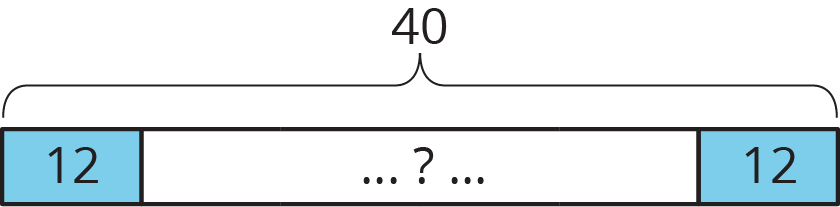
Again, we can think of this in terms of multiplication, with a different factor being the unknown: \(\displaystyle ? \boldcdot 12 = 40\)
Likewise, we can use division to find the unknown: \(\displaystyle 40 \div 12 = \,?\)
Whenever we have a multiplication situation, one factor tells us how many groups there are, and the other factor tells us how much is in each group.
Sometimes we want to find the total. Sometimes we want to find how many groups there are. Sometimes we want to find how much is in each group. Anytime we want to find out how many groups there are or how much is in each group, we can represent the situation using division.