Lesson 11

Using an Algorithm to Divide Fractions

11.1: Multiplying Fractions (5 minutes)

This warm-up revisits multiplication of fractions from grade 5. Students will use this skill as they divide fractions throughout the lesson and the rest of the unit.

Give students 2–3 minutes of quiet work time to complete the questions. Ask them to be prepared to explain their reasoning.

Evaluate each expression.

$\frac 23 \boldcdot 27$
$\frac 12 \boldcdot \frac 23$
$\frac 29 \boldcdot \frac 35$
$\frac {27}{100} \boldcdot \frac {200}{9}$
$\left( 1\frac 34 \right) \boldcdot \frac 57$

For access, consult one of our IM Certified Partners.

Ask a student to share their answer and reasoning to each question, then ask if anyone disagrees. Invite students who disagree to share their explanations. If not mentioned in students' explanations, discuss strategies for multiplying fractions efficiently, how to multiply fractions in which a numerator and a denominator share at least one common factor, and how to multiply mixed numbers.

If students mention "canceling" a numerator and a denominator that share a common factor, demonstrate using the term "dividing" instead. For example, if a student suggests that in the second question ($\frac 12 \boldcdot \frac 23$) the 2 in $\frac 12$ and the 2 in the $\frac 23$ "cancel out", rephrase the statement by saying that dividing the 2 in the numerator by the 2 in the denominator gives us 1, and multiplying by 1 does not change the other numerator or denominator.

11.2: Dividing a Fraction by a Fraction (15 minutes)

This is the final task in a series that leads students toward a general procedure for dividing fractions. Students verify previous observations about the steps for dividing non-unit fractions (namely, multiplying by the denominator and dividing by the numerator) and contrast the results with those found using diagrams. They then generalize these steps as an algorithm and apply it to answer other division questions.

As students discuss in their groups, listen to their observations and explanations. Select students with clear explanations to share later.

Digital

Arrange students in groups of 2. Give students 5–7 minutes of quiet think time and 2–3 minutes to share their response with their partner. Provide access to colored pencils. Some students may find it helpful to identify whole groups and partial groups on a tape diagram by coloring.

Students using the digital materials can use an applet to investigate division of fractions.

Representation: Internalize Comprehension. Provide additional examples and counterexamples to illustrate concepts. Students may benefit from additional examples of division problems that they can “test” to reinforce understanding of their conclusion about how to divide a number by any fraction.
Supports accessibility for: Visual-spatial processing; Organization

Conversing, Representing: MLR8 Discussion Supports. Provide the following sentence frames for students to use when they share their response with their partner: “I know there are ___ $\frac18$s in $\frac34$ because….”, “I drew the diagram like this ___ because.…”, and “First, I ___ because….”. This will help students produce statements that describe how to divide a number by any fraction.
Design Principle(s): Cultivate conversation; Support sense-making

Work with a partner. One person works on the questions labeled “Partner A” and the other person works on those labeled “Partner B.”

Partner A:

Find the value of each expression by completing the diagram.
1. $\frac 34 \div \frac 18$
  
  How many $\frac 18$s in $\frac 34$?
  
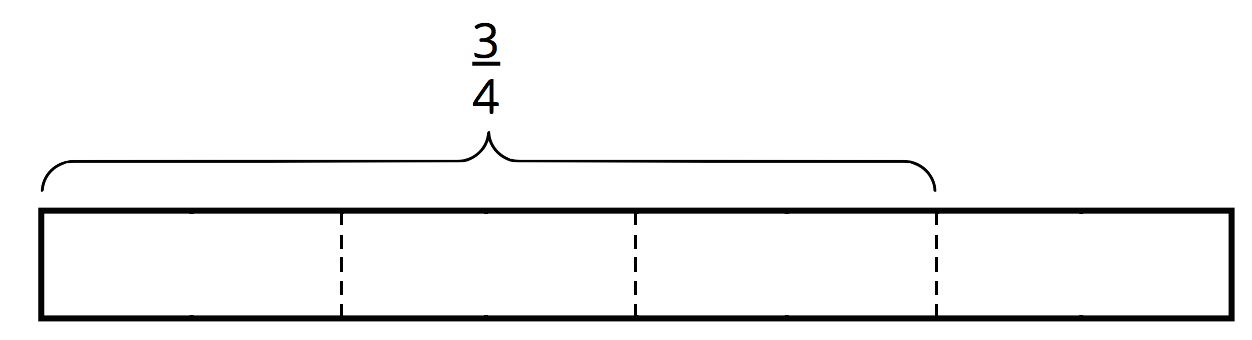
  $Fraction bar diagram. 4 equal parts. First 3 parts labeled the fraction 3 over 4.$
2. $\frac {9}{10} \div \frac 35$
  
  How many $\frac 35$s in $\frac{9}{10}$?
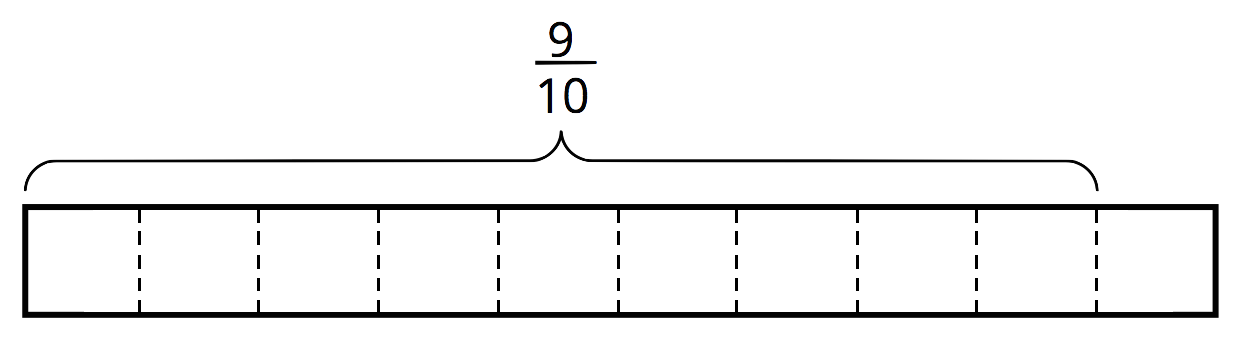
Use the applet to confirm your answers and explore your own examples.

Partner B:

Elena said: “If I want to divide 4 by $\frac 25$, I can multiply 4 by 5 and then divide it by 2 or multiply it by $\frac 12$.”

Find the value of each expression using the strategy Elena described.
1. $\frac 34 \div \frac 18$
2. $\frac{9}{10} \div \frac35$
What do you notice about the diagrams and expressions? Discuss with your partner.
Complete this sentence based on what you noticed:

To divide a number $n$ by a fraction $\frac {a}{b}$, we can multiply $n$ by ________ and then divide the product by ________.
Select all equations that represent the statement you completed.
$n \div \frac {a}{b} = n \boldcdot b \div a$

$n \div \frac {a}{b}= n \boldcdot a \div b$
$n \div \frac {a}{b} = n \boldcdot \frac {a}{b}$

$n \div \frac {a}{b} = n \boldcdot \frac {b}{a}$

For access, consult one of our IM Certified Partners.

Students using the digital materials can use an applet to investigate division of fractions.

Work with a partner. One person works on the questions labeled “Partner A” and the other person works on those labeled “Partner B.”

Partner A: Find the value of each expression by completing the diagram.
1. $\frac 34 \div \frac 18$
  
  How many $\frac 18$s in $\frac 34$?
  
  $Fraction bar diagram. 4 equal parts. First 3 parts labeled the fraction 3 over 4.$
2. $\frac {9}{10} \div \frac 35$
  
  How many $\frac 35$s in $\frac{9}{10}$?
Partner B:

Elena said, “If I want to divide 4 by $\frac 25$, I can multiply 4 by 5 and then divide it by 2 or multiply it by $\frac 12$.”

Find the value of each expression using the strategy Elena described.
1. $\frac 34 \div \frac 18$
2. $\frac{9}{10} \div \frac35$
What do you notice about the diagrams and expressions? Discuss with your partner.
Complete this sentence based on what you noticed:

To divide a number $n$ by a fraction $\frac {a}{b}$, we can multiply $n$ by ________ and then divide the product by ________.
Select all the equations that represent the sentence you completed.
- $n \div \frac {a}{b} = n \boldcdot b \div a$
- $n \div \frac {a}{b}= n \boldcdot a \div b$
- $n \div \frac {a}{b} = n \boldcdot \frac {a}{b}$
- $n \div \frac {a}{b} = n \boldcdot \frac {b}{a}$

For access, consult one of our IM Certified Partners.

Invite a couple of students to share their conclusion about how to divide a number by any fraction. Then, review the sequence of reasoning that led us to this conclusion using both numerical examples and algebraic statements throughout. Remind students that in the past few activities, we learned that:

Dividing by a whole number $n$ is the same as multiplying by a unit fraction $\frac{1}{n}$ (e.g., dividing by 5 is the same as multiplying by $\frac15$).
Dividing by a unit fraction $\frac{1}{n}$ is the same as multiplying by a whole number $n$ (e.g., dividing by $\frac 17$ is the same as multiplying by 7).
Dividing by a fraction $\frac{a}{b}$ is the same as multiplying by a unit fraction $\frac{1}{a}$ and multiplying by a whole number $b$, which is the same as multiplying by $\frac ba$ (e.g., dividing by $\frac57$ is the same as multiplying by $\frac 15$, and then by 7. Performing these two steps gives the same result as multiplying by $\frac75$).

Finish the discussion by trying out the generalized method with other fractions such a $18\div\frac97$, or $\frac{15}{14}\div\frac{5}{2}$. Explain that although we now have a reliable and efficient method to divide any number by any fraction, sometimes it is still easier and more natural to think of the quotient in terms of a multiplication problem with a missing factor and to use diagrams to find the missing factor.

11.3: Using an Algorithm to Divide Fractions (15 minutes)

This activity allows students to practice using the algorithm from earlier to solve division problems that involve a wider variety of fractions. Students can use any method of reasoning and are not expected to use the algorithm. As they encounter problems with less-friendly numbers, however, they notice that it becomes more challenging to use diagrams or other concrete strategies, and more efficient to use the algorithm. As they work through the activity, students choose their method.

Monitor the strategies students use and identify those with different strategies— including those who may not have used the algorithm—so they can share later.

Keep students in groups of 2. Give students 5–7 minutes of quiet work time, followed by 2–3 minutes to discuss their responses with a partner.

Representation: Internalize Comprehension. Activate or supply background knowledge. Provide students with access to blank tape diagrams. Encourage students to attempt more than one strategy for at least one of the problems.
Supports accessibility for: Visual-spatial processing; Organization

Calculate each quotient. Show your thinking and be prepared to explain your reasoning.

$\frac 89 \div 4$
$\frac 34 \div \frac 12$
$3 \frac13 \div \frac29$
$\frac92 \div \frac 38$
$6 \frac 25 \div 3$
After biking $5 \frac 12$ miles, Jada has traveled $\frac 23$ of the length of her trip. How long (in miles) is the entire length of her trip? Write an equation to represent the situation, and then find the answer.

For access, consult one of our IM Certified Partners.

Are you ready for more?

Suppose you have a pint of grape juice and a pint of milk. You pour 1 tablespoon of the grape juice into the milk and mix it up. Then you pour 1 tablespoon of this mixture back into the grape juice. Which liquid is more contaminated?

For access, consult one of our IM Certified Partners.

Select previously identified students to share their responses. Sequence their presentations so that students with the more concrete strategies (e.g., drawing pictures) share before those with more abstract strategies. Students using the algorithm should share last. Find opportunities to connect the different methods. For example, point out where the multiplication by a denominator and division by a numerator are visible in a tape diagram.

Conversing, Representing: MLR7 Compare and Connect. As students consider the different strategies, invite them to make connections between the various representations and approaches. Ask, “What do each of the strategies have in common?”, “How are the strategies different?” and “Which strategy is more efficient? Why?” Listen for and amplify observations that include mathematical language and reasoning.
Design Principle(s): Maximize meta-awareness; Optimize output (for comparison)

Lesson Synthesis

In this lesson, we noticed a more-efficient way to divide fractions. We found that to divide $\frac32$ by $\frac 25$, for example, we can multiply $\frac 32$ by 5 and then by $\frac 12$, or simply multiply $\frac32$ by $\frac52$.

Let's see how this is the same or different than finding the quotient using tape diagrams. (If time permits, consider illustrating each diagram for all to see.)

“Suppose we interpret $\frac32 \div \frac 25$ to mean ‘how many $\frac 25$ are in $\frac 32$?’ and use a tape diagram to find the answer. Where do we see the multiplication by 5 and by $\frac 12$ in the diagramming process?” (We draw a diagram to represent $\frac 32$ and draw equal parts, each with a value of $\frac15$. We count how many groups of $\frac25$ there are. Partitioning into fifths gives as 5 times as many parts. This is the multiplication by 5. Counting by two-fifths leads to half as many parts. This is the multiplication by $\frac12$.)
“Suppose we interpret $\frac32 \div \frac 25$ to mean ‘$\frac 25$ of what number is $\frac32$?’ and use a tape diagram to find the answer. Where do we see the multiplication by 5 and by $\frac 12$ in the diagramming process?” (We draw a tape diagram to represent a whole group. We mark two-fifths of it as having a value of $\frac 32$. We divide that value by 2 (or multiply by $\frac12$) to find one fifth of a group. To find out how much is in the whole group, we multiply by 5.)

Note that in both cases, there is a multiplication by $\frac 12$ and another multiplication by 5, which is the same as multiplication by $\frac 52$. Highlight that dividing by $\frac ab$ is equivalent to multiplying by $b$ and then by $\frac 1a$, or simply multiplying by $\frac ba$ (the reciprocal of $\frac ab$). This is true whether we interpreted the division problem in terms of finding the number of groups or finding the size of a group.

11.4: Cool-down - Watering A Fraction of House Plants (5 minutes)

For access, consult one of our IM Certified Partners.

Student Lesson Summary

The division $a \div \frac34 = {?}$ is equivalent to $\frac 34 \boldcdot {?} = a$, so we can think of it as meaning “$\frac34$ of what number is $a$?” and represent it with a diagram as shown. The length of the entire diagram represents the unknown number.

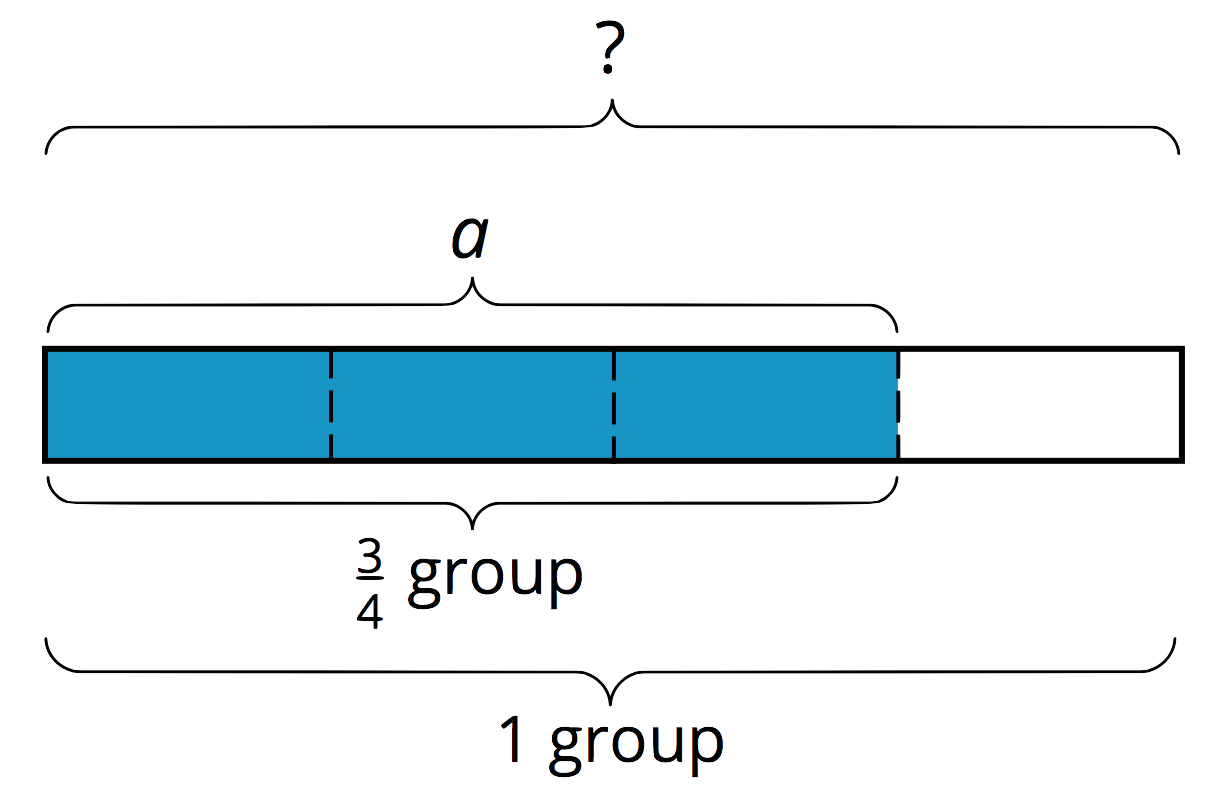
Fraction bar diagram. 4 equal parts. 3 parts shaded.

If $\frac34$ of a number is $a$, then to find the number, we can first divide $a$ by 3 to find $\frac14$ of the number. Then we multiply the result by 4 to find the number.

The steps above can be written as: $a \div 3 \boldcdot 4$. Dividing by 3 is the same as multiplying by $\frac13$, so we can also write the steps as: $a \boldcdot \frac13 \boldcdot 4$.

In other words: $a \div 3 \boldcdot 4= a \boldcdot \frac13 \boldcdot 4$. And $a \boldcdot \frac13 \boldcdot 4 = a \boldcdot \frac43$, so we can say that: $\displaystyle a \div \frac34= a \boldcdot \frac43$

In general, dividing a number by a fraction $\frac{c}{d}$ is the same as multiplying the number by $\frac{d}{c}$, which is the reciprocal of the fraction.

Lesson 11

11.1: Multiplying Fractions (5 minutes)

Warm-up

Launch

Student Facing

Student Response

Activity Synthesis

11.2: Dividing a Fraction by a Fraction (15 minutes)

Activity

Launch

Student Facing

Student Response

Launch

Student Facing

Student Response

Activity Synthesis

11.3: Using an Algorithm to Divide Fractions (15 minutes)

Activity

Launch

Student Facing

Student Response

Student Facing

Are you ready for more?

Student Response

Activity Synthesis

Lesson Synthesis

Lesson Synthesis

11.4: Cool-down - Watering A Fraction of House Plants (5 minutes)

Cool-Down

Student Lesson Summary

Student Facing