Lesson 13
Rectangles with Fractional Side Lengths
Let’s explore rectangles that have fractional measurements.
13.1: Areas of Squares

- What do you notice about the areas of the squares?
- Kiran says “A square with side lengths of \(\frac13\) inch has an area of \(\frac13\) square inches.” Do you agree? Explain or show your reasoning.
13.2: Areas of Squares and Rectangles
Your teacher will give you graph paper and a ruler.
-
On the graph paper, draw a square with side lengths of 1 inch. Inside this square, draw another square with side lengths of \(\frac14\) inch.
Use your drawing to answer the questions.
- How many squares with side lengths of \(\frac 14\) inch can fit in a square with side lengths of 1 inch?
- What is the area of a square with side lengths of \(\frac 14\) inch? Explain or show your reasoning.
-
On the graph paper, draw a rectangle that is \(3\frac12\) inches by \(2\frac14\) inches.
For each question, write a division expression and then find the answer.
- How many \(\frac14\)-inch segments are in a length of \(3\frac12\) inches?
- How many \(\frac14\)-inch segments are in a length of \(2\frac14\) inches?
- Use your drawing to show that a rectangle that is \(3\frac12\) inches by \(2\frac14\) inches has an area of \(7\frac78\) square inches.
13.3: Areas of Rectangles
Each of these multiplication expressions represents the area of a rectangle.
\(2 \boldcdot 4\)
\(2\frac12 \boldcdot 4\)
\(2 \boldcdot 4\frac 34\)
\(2\frac12 \boldcdot 4\frac34\)
-
All regions shaded in light blue have the same area. Match each diagram to the expression that you think represents its area. Be prepared to explain your reasoning.
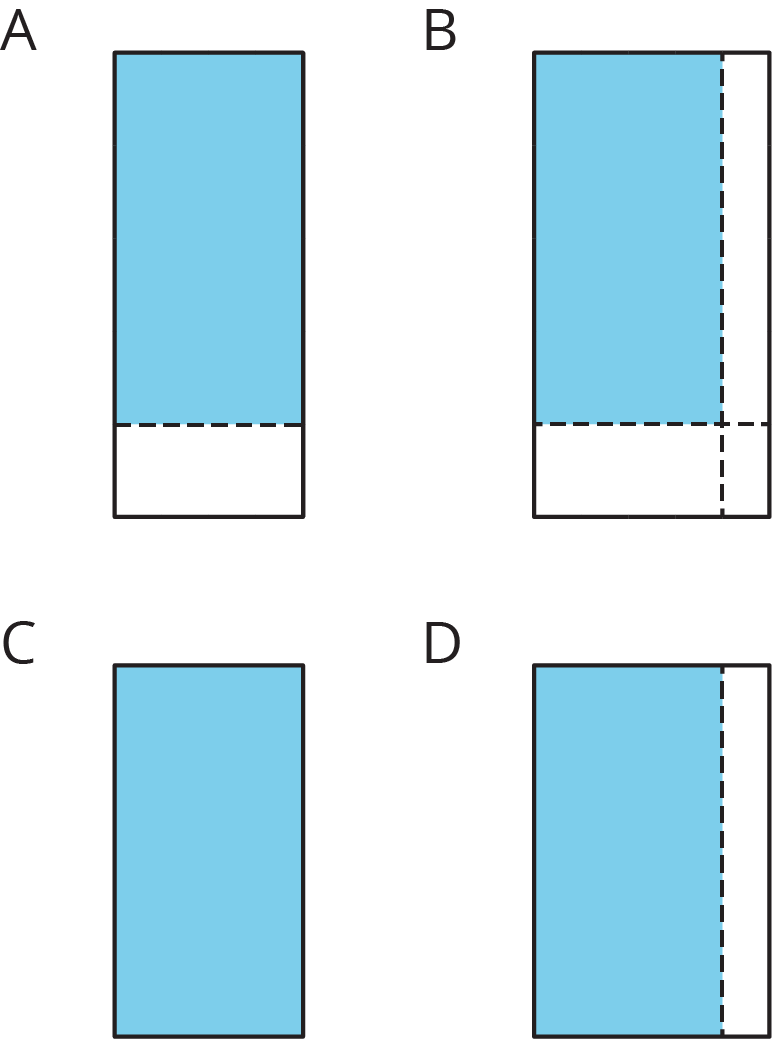
- Use the diagram that matches \(2\frac12 \boldcdot 4\frac34\) to show that the value of \(2\frac12 \boldcdot 4\frac34\) is \(11\frac78\).
The following rectangles are composed of squares, and each rectangle is constructed using the previous rectangle. The side length of the first square is 1 unit.

-
Draw the next four rectangles that are constructed in the same way. Then complete the table with the side lengths of the rectangle and the fraction of the longer side over the shorter side.
short side long side \(\frac {\text {long side}}{\text{short side}}\) 1 1 2 3 - Describe the values of the fraction of the longer side over the shorter side. What happens to the fraction as the pattern continues?
13.4: How Many Would it Take? (Part 2)
Noah would like to cover a rectangular tray with rectangular tiles. The tray has a width of \(11\frac14\) inches and an area of \(50\frac58\) square inches.
- Find the length of the tray in inches.
- If the tiles are \(\frac{3}{4}\) inch by \(\frac{9}{16}\) inch, how many would Noah need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.
- Draw a diagram to show how Noah could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but does not need to show every tile.
Summary
If a rectangle has side lengths \(a\) units and \(b\) units, the area is \(a \boldcdot b\) square units. For example, if we have a rectangle with \(\frac12\)-inch side lengths, its area is \(\frac12 \boldcdot \frac12\) or \(\frac14\) square inches.

This means that if we know the area and one side length of a rectangle, we can divide to find the other side length.

If one side length of a rectangle is \(10\frac12\) in and its area is \(89\frac14\) in2, we can write this equation to show their relationship: \(\displaystyle 10\frac12 \boldcdot {?} =89\frac14\)
Then, we can find the other side length, in inches, using division: \(\displaystyle 89\frac14 \div 10\frac12 = {?}\)