Lesson 10
Dividing by Unit and Non-Unit Fractions
Problem 1
Priya is sharing 24 apples equally with some friends. She uses division to determine how many people can have a share if each person gets a particular number of apples. For example, \(24 \div 4 = 6\) means that if each person gets 4 apples, then 6 people can have apples. Here are some other calculations:
\(24 \div 4 = 6\)
\(24 \div 2 = 12\)
\(24 \div 1 = 24\)
\(24 \div \frac12 = {?}\)
-
Priya thinks the “?” represents a number less than 24. Do you agree? Explain or show your reasoning.
- In the case of \(24 \div \frac12 = {?}\), how many people can have apples?
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Here is a centimeter ruler.
- Use the ruler to find \(1 \div \frac{1}{10}\) and \(4 \div \frac{1}{10}\).
-
What calculation did you do each time?
-
Use this pattern to find \(18 \div \frac{1}{10}\).
- Explain how you could find \(4\div \frac{2}{10}\) and \(4\div \frac{8}{10}\).
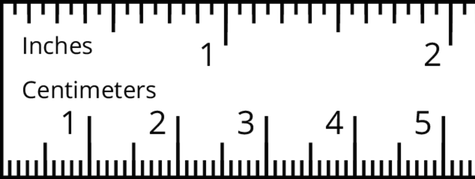
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Find each quotient.
- \(5 \div \frac{1}{10}\)
- \(5 \div \frac{3}{10}\)
- \(5\div \frac{9}{10}\)
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Use the fact that \(2\frac12 \div \frac18=20\) to find \(2\frac12 \div \frac58\). Explain or show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Consider the problem: It takes one week for a crew of workers to pave \(\frac35\) kilometer of a road. At that rate, how long will it take to pave 1 kilometer?
Write a multiplication equation and a division equation to represent the question. Then find the answer and show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 9.)Problem 6
A box contains \(1\frac 34\) pounds of pancake mix. Jada used \(\frac 78\) pound for a recipe. What fraction of the pancake mix in the box did she use? Explain or show your reasoning. Draw a diagram, if needed.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 7.)Problem 7
Calculate each percentage mentally.
- 25% of 400
- 50% of 90
- 75% of 200
- 10% of 8,000
- 5% of 20
Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 14.)