Lesson 9
Constant Speed
Lesson Narrative
In the previous lesson, students used the context of shopping to explore how equivalent ratios and ratios involving one can be used to find unknown amounts. In this lesson, they revisit these ideas in a new context—constant speed—and through concrete experiences. Students measure the time it takes them to travel a predetermined distance—first by moving slowly, then quickly—and use it to calculate and compare the speed they traveled in meters per second.
Here, double number lines are used to represent the association between distance and time, and to convey the idea of constant speed as a set of equivalent ratios (e.g., 10 meters traveled in 20 seconds at a constant speed means that 0.5 meters is traveled in 1 second, and 5 meters is traveled in 10 seconds). Students come to understand that, like price, speed can be described using the terms per and at this rate.
The idea of a constant speed relating the quantities of distance and time is foundational for the later, more abstract idea of a constant rate, and is important in the development of students’ ability to reason abstractly about quantities (MP2).
Learning Goals
Teacher Facing
- Calculate the distance an object travels in 1 unit of time and express it using a phrase like “meters per second” (orally and in writing).
- For an object moving at a constant speed, use a double number line diagram to represent equivalent ratios between the distance traveled and elapsed time.
- Justify (orally and in writing) which of two objects is moving faster, by identifying that it travels more distance in the same amount of time or that it travels the same distance in less time.
Student Facing
Let’s use ratios to work with how fast things move.
Required Materials
Required Preparation
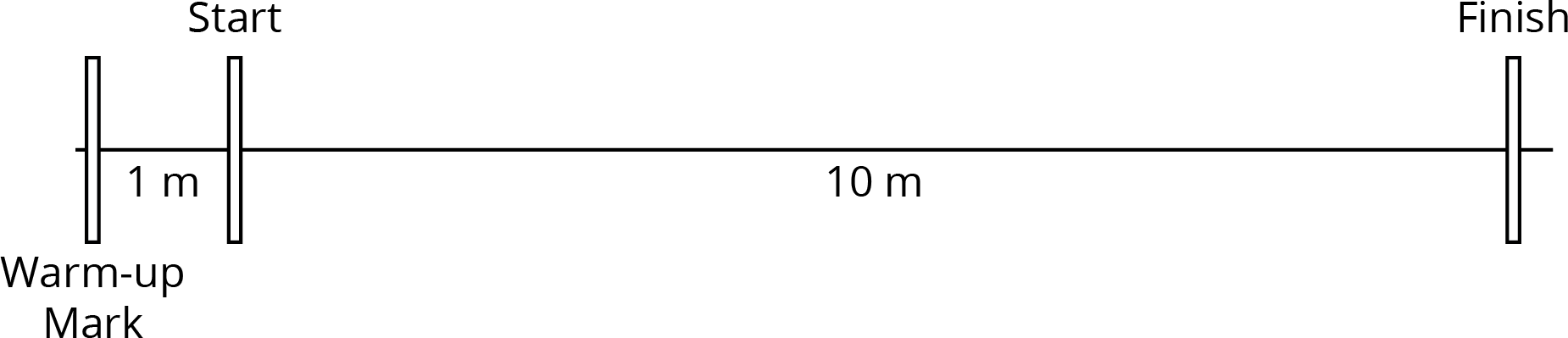
Before class, set up 4 paths with a 1-meter warm-up zone and a 10-meter measuring zone.
Learning Targets
Student Facing
- I can choose and create diagrams to help me reason about constant speed.
- If I know an object is moving at a constant speed, and I know two of these things: the distance it travels, the amount of time it takes, and its speed, I can find the other thing.
CCSS Standards
Glossary Entries
-
meters per second
Meters per second is a unit for measuring speed. It tells how many meters an object goes in one second.
For example, a person walking 3 meters per second is going faster than another person walking 2 meters per second.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |