Lesson 12
Navigating a Table of Equivalent Ratios
12.1: Number Talk: Multiplying by a Unit Fraction (10 minutes)
Warm-up
The purpose of this number talk is to encourage students to use the meaning of fractions and the properties of operations to find the product of fractions and decimals.
In grade 4, students multiplied a fraction by a whole number, reasoning about these problems based on their understandings of multiplication as groups of a number. In grade 5, students multiply fractions by whole numbers, reasoning in terms of taking a part of a part, whether that be by using division or partitioning a whole. In both grade levels, the context of the problem played a significant role in how students reasoned and notated the problem and solution. Based on these understandings, two ideas will be relevant to future work in the unit and are important to emphasize during discussions:
- Dividing by a number is the same as multiplying by its reciprocal.
- The commutative property of multiplication can help us solve a problem regardless of the context.
Launch
Display one problem at a time. Tell students to give a signal when they have an answer and a strategy. After each problem, give students 1 minute of quiet think time and follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find the product mentally.
\(\frac13\boldcdot 21\)
\(\frac16 \boldcdot 21\)
\((5.6) \boldcdot \frac18\)
\(\frac14\boldcdot (5.6)\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see. Ask students if or how the factors in the problem impacted their strategy choice. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone solve the problem the same way but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
Design Principle(s): Optimize output (for explanation)
12.2: Comparing Taco Prices (10 minutes)
Activity
The purpose of this activity is to encourage students to use a table to find the price for one taco for two different situations. Students are likely to divide the cost of the tacos by the number of tacos to find the cost for one taco, which is appropriate. Use the opportunity to remind students that dividing by a whole number is the same as multiplying by its reciprocal (a unit fraction). This insight will come in handy in future activities and lessons.
Launch
Tell students that we usually use tables to show equivalent ratios, but since we do not know in advance whether the ratios of number of tacos to price will be the same, we might want to keep track of them in separate tables.
Arrange students in groups of 2. Give students 3 minutes of quiet think time, and then time to discuss their responses and reasoning with their partner.
Design Principle(s): Cultivate conversation; Support sense-making
Student Facing
| number of tacos | price in dollars |
|---|---|
Use the table to help you solve these problems. Explain or show your reasoning.
- Noah bought 4 tacos and paid \$6. At this rate, how many tacos could he buy for \$15?
- Jada’s family bought 50 tacos for a party and paid \$72. Were Jada’s tacos the same price as Noah’s tacos?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The focus should be on how students found the cost of a single taco in each situation. Be sure to remind students that dividing by a whole number is the same as multiplying by its reciprocal (a unit fraction).
12.3: Hourly Wages (10 minutes)
Activity
This task introduces students to the strategy of using an equivalent ratio with one quantity having a value of 1 to find other equivalent ratios. Students look at a worked-out example of the strategy, make sense of how it works, and later apply it to solve other problems.
There are a couple of key insights to uncover here:
- The ratios we deal with do not always have corresponding quantities that are multiples of each other (e.g., in the task, 5 is not a multiple of 8, or vice versa).
- In those situations, finding an equivalent ratio where one of the quantities is 1 can be a helpful intermediate step.
Also highlighted and reinforced here is an idea students learned in Grade 5, that dividing by a whole number is equivalent to multiplying by its reciprocal (e.g., dividing by 5 is the same as multiplying by \(\frac15\)).
Expect some students to initially overlook the benefit of using a ratio involving a “1,” to rely on methods from previous work, and to potentially get stuck (especially when dealing with a decimal value in the last row). For example, since the table shows an arrow and a multiplication from the first to the second row and from the second to third, students may try to do the same to find the missing value in the fourth row. While finding a factor that can be multiplied to 8 to obtain 3 is valid, encourage students to consider an alternative, given what they already know about the situation (i.e., how much the person earned in 1 hour). If needed, scaffold their thinking by asking how much Lin would earn in 2 hours and then in 3 hours.
Identify a student or two who can articulate why \(\frac15\) is used as a multiplier. Also notice those who can correctly reason why using a ratio with one of the values being 1 helps to find other equivalent ratios and students who reason differently. Invite these students to share later.
Launch
This may be some students’ first time reasoning about money earned by the hour. Take a minute to ensure everyone understands the concept. Ask if anyone has earned money based on the number of hours doing a job. Some students may have experience being paid by the hour for helping with house cleaning, a family business, babysitting, dog walking, or doing other jobs.
Give students quiet think time to complete the activity and a minute to share their responses (especially to the last two questions) with a partner before discussing as a class.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Lin is paid $90 for 5 hours of work. She used the table to calculate how much she would be paid at this rate for 8 hours of work.
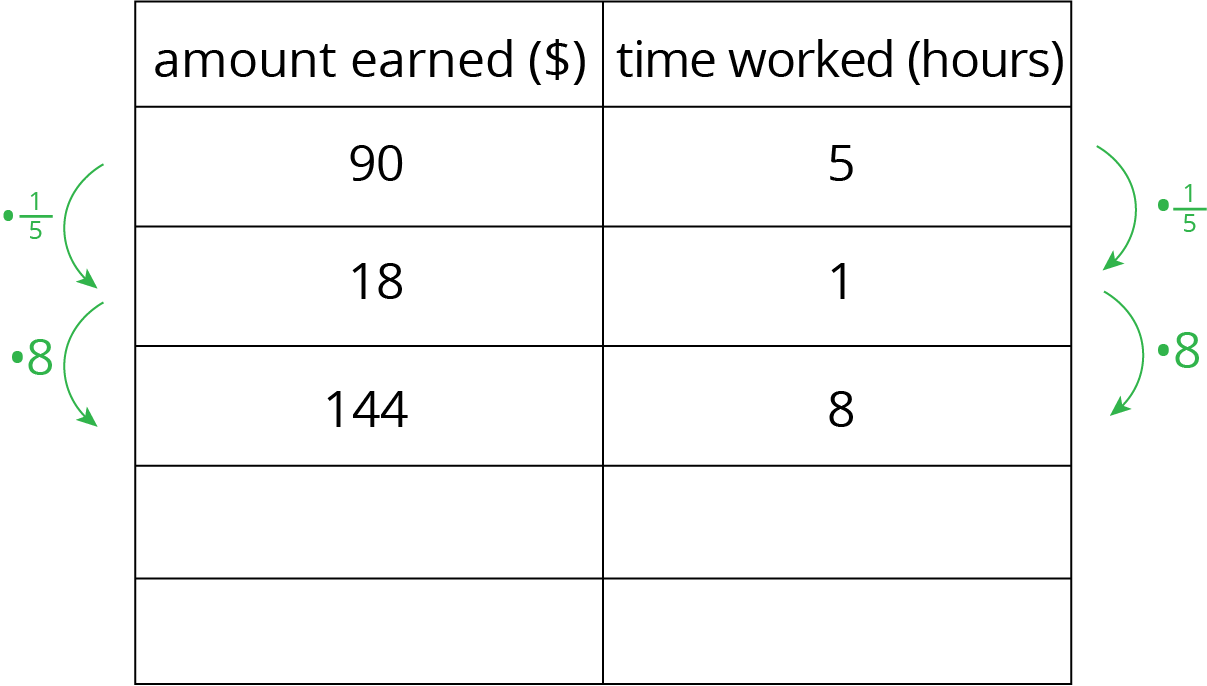
- What is the meaning of the 18 that appears in the table?
- Why was the number \(\frac15\) used as a multiplier?
- Explain how Lin used this table to solve the problem.
-
At this rate, how much would Lin be paid for 3 hours of work? For 2.1 hours of work?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select a few students to share about the use of \(\frac15\) as a multiplier and to explain the reasoning process shown in the table. If different approaches are used, take the opportunity to compare and contrast the efficacy of each.
If students had trouble reasoning to find the pay for 2.1 hours of work, help them articulate what they have done in each preceding case and urge them to think about the 2.1 the same way. If they are unsure whether multiplying 18 by 2.1 would work, encourage them to check whether the answer makes sense. (For two hours of work, Lin would earn $36, so it stands to reason that she would earn a bit more than $36 for 2.1 hours.) In doing so, students practice decontextualizing and contextualizing their reasoning and solutions (MP2).
12.4: Zeno’s Memory Card (15 minutes)
Optional activity
Previously, students explored the limitation of a double number line when dealing with greatly scaled-up ratios; they saw that extending the number lines can be impractical. Here, they encounter a situation involving significantly scaled-down ratios, in which a double number line is likewise impractical (i.e., there is not enough room to fit relevant information) and see that a table is clearly preferable.
The given table deliberately includes more rows than necessary to answer the question. Some students may realize that it is not necessary to fill in all the rows if they use a different factor in finding equivalent ratios. Notice students who take such shortcuts so they can share later. Their reasoning can further highlight the flexibility of a table.
Launch
Open the task with a request for two volunteers and a question. Have the volunteers stand at different distances from a wall but with a clear path toward it.
Ask: “Can either student reach the wall if every time they make a move toward it, they only move half the distance between them and the wall?”
Give students a moment to think and share their predictions with a partner. Without further explanations, ask the two volunteers to begin their halfway-at-a-time journey toward the wall. When the wall is within an arm’s reach, ask the volunteers to stop. Select two students who made different predictions—one who thought it was impossible to reach the wall and one who thought otherwise—to share their reasoning. If one opinion is not represented, share the reasoning for it yourself.
Explain that the situation at hand is a famous paradox, credited to an ancient Greek philosopher, Zeno of Elea (c. ~450 BCE). Tell students: “A paradox is a situation that both cannot be true and must be true at the same time. Going halfway toward a destination is one of Zeno’s paradoxes.”
Explain that it is both impossible and possible to reach the wall by following this go-halfway procedure. Because some distance, although increasingly small, will always be left by constantly going halfway, we say it is impossible to reach the wall. But it is also obvious that the volunteers can get close enough to touch the wall, thereby “reaching” the wall.
Tell students that the next task also uses a “go halfway” process, but in a different context.
Supports accessibility for: Memory; Conceptual processing
Student Facing
In 2016, 128 gigabytes (GB) of portable computer memory cost $32.
-
Here is a double number line that represents the situation:

One set of tick marks has already been drawn to show the result of multiplying 128 and 32 each by \(\frac12\). Label the amount of memory and the cost for these tick marks.
Next, keep multiplying by \(\frac12\) and drawing and labeling new tick marks, until you can no longer clearly label each new tick mark with a number.
-
Here is a table that represents the situation. Find the cost of 1 gigabyte. You can use as many rows as you need.
memory (gigabytes) cost (dollars) 128 32 - Did you prefer the double number line or the table for solving this problem? Why?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A kilometer is 1,000 meters because kilo is a prefix that means 1,000. The prefix mega means 1,000,000 and giga (as in gigabyte) means 1,000,000,000. One byte is the amount of memory needed to store one letter of the alphabet. About how many of each of the following would fit on a 1-gigabyte flash drive?
- letters
- pages
- books
- movies
- songs
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Watch out for students being overly precise or wildly imprecise with drawing tick marks on their double number line diagram. We want them to eyeball approximately half the distance, but it would be too time-consuming to measure precisely.
Activity Synthesis
The discussion should center around why the table was easier to use for this problem: the numbers we started with were so large that there wasn’t enough room to locate 1 gigabyte on the number line.
If any students multiplied the ratios by a fraction other than \(\frac12\) so that they did not have to fill all the rows, consider highlighting this shortcut. (They could even divide 128 and 32 by 128 to arrive at an answer directly, using what they have learned about unit price.) It shows how the table enables reasoning with numbers (rather than with lengths) and is more flexible.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
This lesson is about using a table of equivalent ratios in an efficient way. To wrap up, highlight a few important points:
- In problems with equivalent ratios, finding an equivalent ratio containing a “1” is often a good strategy.
- To create a new row in a table of equivalent ratios, take an existing row and multiply both values by the same number.
- Remember that we can multiply whole numbers by unit fractions to get smaller numbers.
12.5: Cool-down - Price of Bagels (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
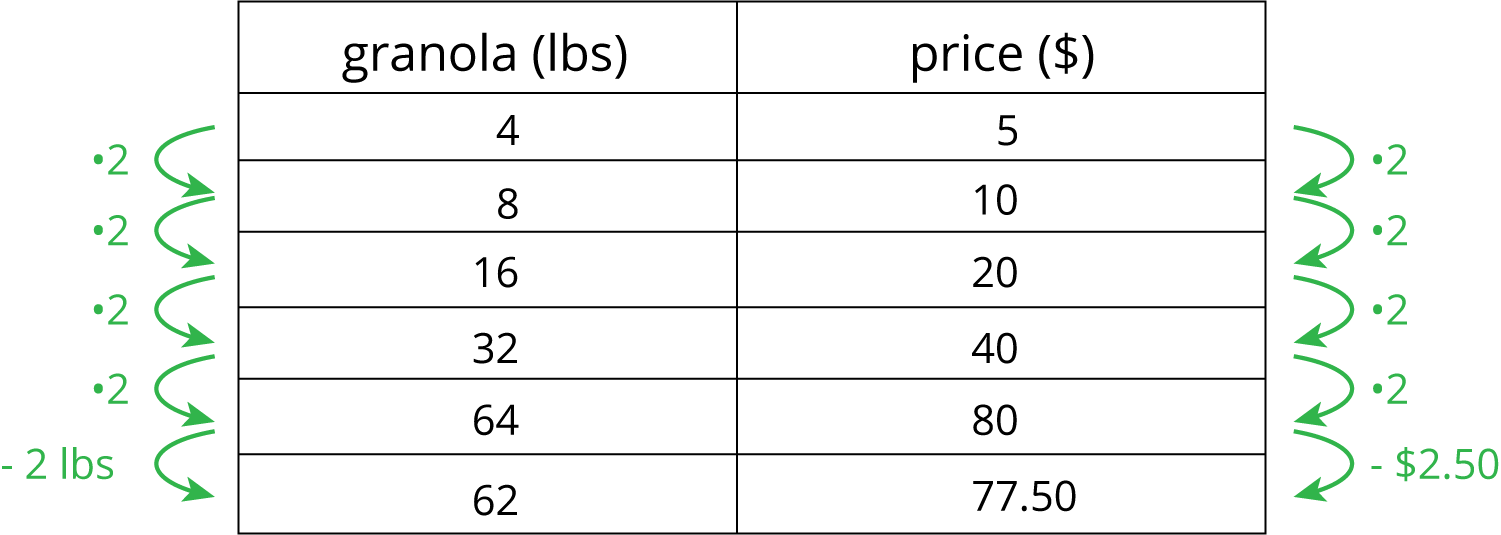
Finding a row containing a “1” is often a good way to work with tables of equivalent ratios. For example, the price for 4 lbs of granola is \$5. At that rate, what would be the price for 62 lbs of granola?
Here are tables showing two different approaches to solving this problem. Both of these approaches are correct. However, one approach is more efficient.
-
Less efficient
-
More efficient
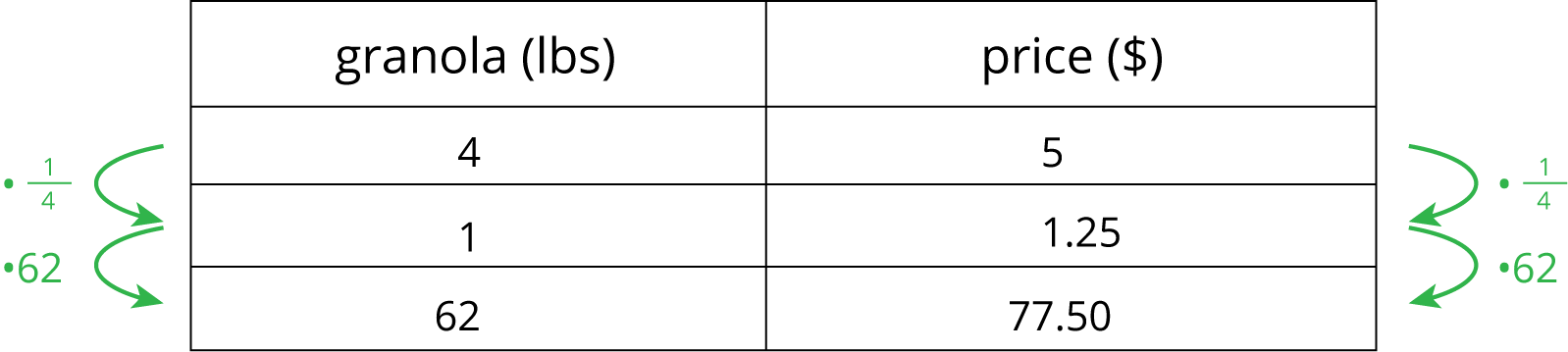
Notice how the more efficient approach starts by finding the price for 1 lb of granola.
Remember that dividing by a whole number is the same as multiplying by a unit fraction. In this example, we can divide by 4 or multiply by \(\frac14\) to find the unit price.