Lesson 16
Solving More Ratio Problems
16.1: You Tell the Story (10 minutes)
Warm-up
This warm-up reminds students of previous work with tape diagrams and encourages a different way to reason with them. Students are given only a tape diagram and are asked to generate a concrete context to go with the representation.
Students’ stories should have the following components:
- the same unit for both quantities in the ratio
- a ratio of \(7:3\)
- scaling by 3, or 3 units per part
- They may also have a quantity of 30 that represents the sum of the two quantities in the ratio.
As students work, identify a few different students whose stories are clearly described and are consistent with the diagram so that they can share later.
Launch
Ask students to share a few things they remember about tape diagrams from the previous lesson. Students may recall that:
- We draw one tape for every quantity in the ratio. Each tape has parts that are the same size.
- We draw as many parts as the numbers in the ratio show (e.g., a \(2:3\) ratio: we draw 2 parts in a tape and 3 parts in another tape).
- Each part represents the same value.
- Tape diagrams can be used to think about a ratio of parts and the total amount.
Tell students their job is to come up with a valid situation to match a given tape diagram. Give students some quiet thinking time, and then time to share their response with a partner.
Student Facing
Describe a situation with two quantities that this tape diagram could represent.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may misunderstand the meaning of the phrase “with two quantities” and simply come up with a situation involving ten identical groups of three. Point out that the phrase means that the row of seven groups of three should represent something different than the row of three groups of three.
Students may also come up with a situation involving different units, for example, quantity purchased and cost, or distance traveled and time elapsed. Remind them that the parts of tape are meant to represent the same value, so we need a situation that uses the same units for both parts of the ratio.
Activity Synthesis
Invite a few students to share their stories with the class. As they share, consider recording key details about each story for all students to see. Then, ask students to notice similarities in the different scenarios.
Guide students to see that they all involve the same units for both quantities of the ratio, a ratio of 7 to 3, and either 3 units per part or scaling by 3. They may also involve an amount of 30 units, representing the sum of the two quantities.
16.2: A Trip to the Aquarium (20 minutes)
Activity
This task prompts students to solve a single problem using a triple number line, a table, or a tape diagram. Either assign each student a representation or allow students to choose the representation they prefer. During the following discussion, they will compare and contrast the three representations and identify the relative merits of the different representations for the different problems.
Students will have varying opinions about which representation they prefer and why. Their views may stem from observations such as:
- Number lines and tables involve scaling up individual quantities to find the total. Tape diagrams involve starting with the total and breaking it down into equal groups.
- It is hard to take shortcuts with number line diagrams.
- We can use the number line diagram or the table efficiently by thinking, “17 times what is 85?” This value tells us how many “batches” of tickets the teacher had to order.
- When using a tape diagram, it was easier to count 17 groups and compute \(85\div17\) to find how many tickets each group needs.
Students may struggle to represent the problem with a tape diagram. As they work, notice any trends that may need to be addressed with the class.
Launch
Tell students that they will now solve a ratio problem in one of three different ways. Either assign each student one of the representations or instruct them to choose one representation to use.
Give students quiet think time to complete the activity and then, optionally, time to share their responses with a small group or in pairs.
Supports accessibility for: Memory; Language
Reading: MLR6 Three Reads. This is one of the first times Math Language Routine 6 is suggested as a support in this course. In this routine, students are supported in reading a mathematical text, situation, or word problem three times, each with a particular focus. During the first read, students focus on comprehending the situation; during the second read, students identify quantities; during the third read, students brainstorm possible strategies to answer the question. The question to be answered does not become a focus until the third read so that students can make sense of the whole context before rushing to a solution. The purpose of this routine is to support students’ reading comprehension as they make sense of mathematical situations and information through conversation with a partner.
Design Principle(s): Support sense-making
How It Happens:
-
In the first read, students read the problem with the goal of comprehending the situation. Do not reveal the questions with the three options for solving at this point.
Invite a student to read the description of the situation aloud while everyone else reads with them and then ask, “What is this situation about?
Allow one minute to discuss with a partner, and then share with the whole class. A clear response would be: “buying tickets for a class trip to an aquarium.”
-
In the second read, students analyze the mathematical structure of the story by naming quantities.
Invite students to read the problem aloud with their partner or select a different student to read to the class and then prompt students by asking, “What can be counted or measured in this situation? For now we don’t need to focus on how many or how much of anything, but what can we count in this situation?” Give students one minute of quiet think time followed by another minute to share with their partner. Quantities may include: total number of tickets bought; number of students; number of chaperones; ratio of chaperones to students.
-
In the third read, students brainstorm possible mathematical strategies to answer the question, “How many tickets are for chaperones, and how many are for students?” (Still do not reveal the three given options for solving.)
Invite students to read the problem aloud with their partner or select a different student to read to the class. Instruct students to think of ways to approach the question without actually solving the problem.
Consider using these questions to prompt students: “What strategy or method would you try first?,” “How could a diagram help you approach this question?,” and “Can you think of a different way to solve it?”
Give students one minute of quiet think time followed by another minute to discuss with their partner. Provide this sentence frame as partners discuss: “One way to approach the question would be to….”
Sample responses include: “I would figure out possibilities for the number of students and number of chaperones and see which one adds up to 85.”, “I know that if I divide 85 by 2, it won’t work because there are more students than chaperones, so the groups are not equal, so I know I have to split it up differently.”, “I would draw a tape diagram to figure out different lengths that fit the ratio of students to chaperones.”, and “I would use a double number line/table to scale up the ratio of students to chaperones.” This will help students concentrate on making sense of the situation before rushing to a solution or method.
-
As partners are discussing their strategies, select 1–2 students to share their ideas with the whole class.
Listen for quantities that were mentioned during the second read, and take note of strategies that make explicit the relationships between number of tickets and number of students, number of tickets and number of chaperones, or number of students and number of chaperones. As students are presenting their strategies to the whole class, create a display that summarizes ideas about the question.
-
Post the display where all students can use it as a reference, and finally reveal the actual problems and ensure that a variety of strategies are chosen by students.
Student Facing
Consider the problem: A teacher is planning a class trip to the aquarium. The aquarium requires 2 chaperones for every 15 students. The teacher plans accordingly and orders a total of 85 tickets. How many tickets are for chaperones, and how many are for students?
-
Solve this problem in one of three ways:
Use a triple number line.
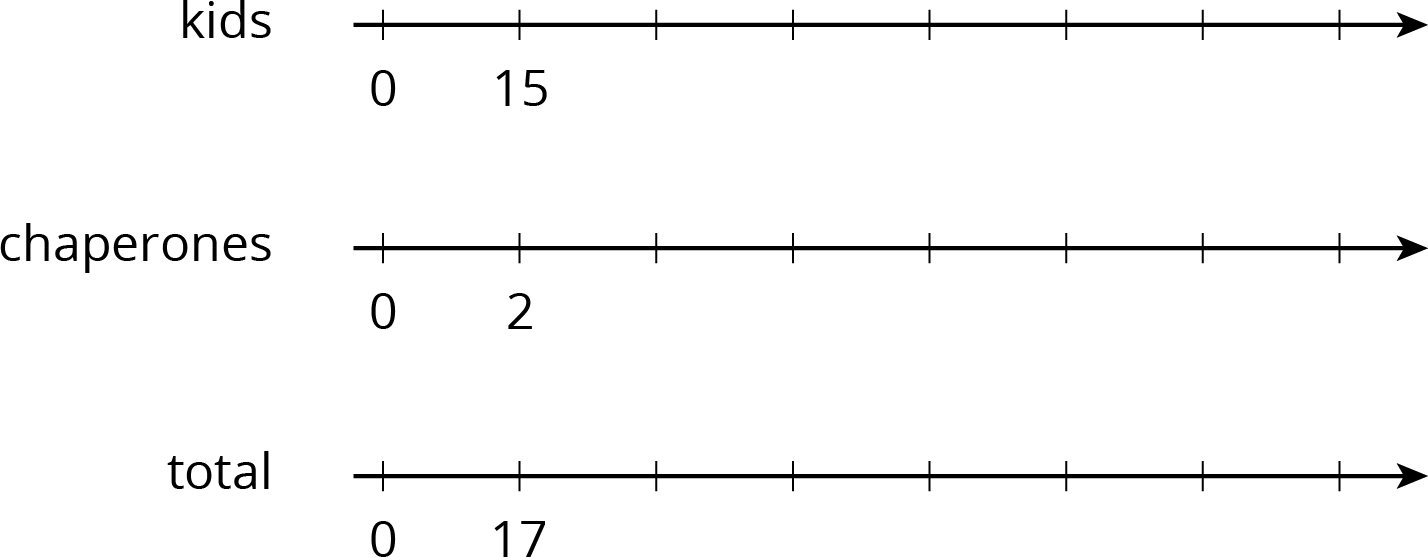
Use a table.
(Fill rows as needed.)kids chaperones total 15 2 17 Use a tape diagram.

- After your class discusses all three strategies, which do you prefer for this problem and why?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Use the digits 1 through 9 to create three equivalent ratios. Use each digit only one time.
\(\boxed{\phantom{3}}:\boxed{\phantom{3}}\) is equivalent to \(\boxed{\phantom{3}}\,\boxed{\phantom{3}}:\boxed{\phantom{3}}\) and \(\boxed{\phantom{3}}\,\boxed{\phantom{3}}:\boxed{\phantom{3}}\,\boxed{\phantom{3}}\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The number line and table representations are organized similarly. For example, one could make progress with both of them simply by skip counting and keeping an eye out for a total of 85 people. The tape diagram, though, is organized in a much different way. Equivalent ratios are not listed out, but rather equivalent ratios arise from thinking about how the diagram could represent any number of batches. Students may thus mistakenly treat the tape diagram like a double number line diagram—they may start writing 15, 30, 45, etc. in the “kids” tape, for example. Once this plays out, students may self-regulate once they notice there are only 2 boxes in the chaperones’ row. But they may decide to just draw more boxes! Reorient these students by asking how many parts of tape there are (17), and reminding them each part of tape represents equal numbers of people, and that there are 85 total people. The presentation of correct work during the discussion could be used as an opportunity to remediate, as well. For example, consider asking a student to explain what they understand about another student’s correct work.
Activity Synthesis
Before debriefing as a class, consider arranging students in groups of 3, where a group includes one student who used each representation. Give them time to see if they got the same answer and compare and contrast the representations.
Solicit students’ reactions to the three strategies, encouraging them to identify what is similar and different about the approaches. Consider polling the class for their preferred strategy. Ask 1–2 students favoring each method to explain why. This can also be a discussion about what worked well in this or that approach, and what might make this or that approach more complete or easy to understand. While there is no right or wrong answer with regards to their preferred strategy, look out for unsupported reasoning or misunderstandings.
Some students may prefer the tape diagram because the solution path seems more direct, but caution them against trying to use a tape diagram any time they see a ratio problem. Because tape diagrams involve equal-sized parts, they can only be used to represent quantities with the same unit. If different units are involved, the parts of one tape and those of the other will not represent an identical quantity.
16.3: Salad Dressing and Moving Boxes (10 minutes)
Activity
This activity gives students a chance to apply the different strategies they have learned to solve ratio problems and to decide on methods that would make the most sense in given situations. If desired, you can have students complete this activity as an info gap, by instructing them to close their books or devices and distributing slips cut from the blackline master. Alternatively, students can simply complete the two problems that are printed in the task statement.
Each problem may lend itself better to a particular representation than to others. Below are sample arguments in support of a representation for each problem, though options may vary:
- The salad dressing problem can be well represented by all three representations because it involves small numbers and simple multiplication.
- The box-moving problem would be inefficient to represent with a number line diagram, since it would require making 8 half-hour jumps to find the total of 72. Either a tape diagram or a table showing more straightforward multiplication would be more efficient.
The time needed to solve the problems may depend on the representation students choose to use.
Launch
Tell students they will continue to practice using the tools at their disposal—number lines, tables, and tape diagrams—to solve ratio problems.
Provide access to graph paper and rulers. Arrange students in groups of 2.
If using the info gap routine: Explain the info gap structure and consider demonstrating the protocol. In each group, distribute a problem card to one student and a data card to the other student. Give students who finish early a different pair of cards and ask them to switch roles.
If not using the info gap routine: Ask students to complete both questions and then compare their strategies with their partner. Partners should work together to resolve any discrepancies.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Cultivate Conversation
Student Facing
Solve each problem, and show your thinking. Organize it so it can be followed by others. If you get stuck, consider drawing a double number line, table, or tape diagram.
- A recipe for salad dressing calls for 4 parts oil for every 3 parts vinegar. How much oil should you use to make a total of 28 teaspoons of dressing?
- Andre and Han are moving boxes. Andre can move 4 boxes every half hour. Han can move 5 boxes every half hour. How long will it take Andre and Han to move all 72 boxes?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
While thinking through problems, it is common for students to hold the meanings of their representations (numbers, quantities, markings, etc.) in their heads without writing them down. When students are getting their solutions ready for others to look at, though, remind them of the importance of labeling quantities and units of measure and making the steps in their thinking clear.
Some students may choose the same strategy or representation each time. If their answers are accurate, this is fine. However, if time allows, ask them to check if they can verify their answer using an alternative strategy.
If using the info gap routine: Students holding a Problem Card may have trouble thinking of appropriate questions to ask their partner. Encourage them to revisit the problem at hand and think about the kinds of information that might be helpful or relevant. (For example, if the problem is about how long it would take to perform something, ask students how they usually gauge the amount of time needed for something. Ask, “What would the amount of time depend on?”)
Activity Synthesis
After students have had time to work, share the correct answers and ask students for their preferences about representations. Some guiding questions:
- “Is there a particular representation you tend to try first?”
- “Does one seem more efficient than the others?”
- “Did the situation in a problem affect your choice? If so, what features of a problem might steer you toward or away from a particular strategy?”
Design Principle(s): Cultivate conversation
Lesson Synthesis
Lesson Synthesis
This lesson was all about understanding that there are different, valid representations to use for problems involving equivalent ratios. For some problems, one representation is easier to use than others. There are no hard and fast rules. As long as the diagram correctly shows the mathematics, and the problem solver can explain it, it’s okay. Some guidelines to draw out are:
- Tape diagrams are most likely to be helpful when the parts of the ratio have the same kind of units and the sum of the quantities is meaningful in the context. For example, cups to cups; miles to miles; boxes moved to boxes moved.
- Number lines are a good choice when it helps to visualize how far apart numbers are from each other. They are harder to use with very big or very small numbers.
- Tables work well in almost all situations. Ask students to articulate good habits when solving equivalent ratio problems with the different representations. Some ideas might include:
- Label each part of the diagram with what it represents.
- Use brackets to indicate total amounts.
- Make sure you read what the question is asking and answer it.
- Make sure you make the answer easy to find.
- Include units in your answer. For example, instead of just writing “4,” write “4 cups.”
16.4: Cool-down - Pizza-making Party (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When solving a problem involving equivalent ratios, it is often helpful to use a diagram. Any diagram is fine as long as it correctly shows the mathematics and you can explain it.
Let’s compare three different ways to solve the same problem: The ratio of adults to kids in a school is \(2:7\). If there is a total of 180 people, how many of them are adults?
-
Tape diagrams are especially useful for this type of problem because both parts of the ratio have the same units (“number of people") and we can see the total number of parts.

This tape diagram has 9 equal parts, and they need to represent 180 people total. That means each part represents \(180 \div 9\), or 20 people.

Two parts of the tape diagram represent adults. There are 40 adults in the school because \(2\boldcdot 20 = 40\).
-
Double or triple number lines are useful when we want to see how far apart the numbers are from one another. They are harder to use with very big or very small numbers, but they could support our reasoning.
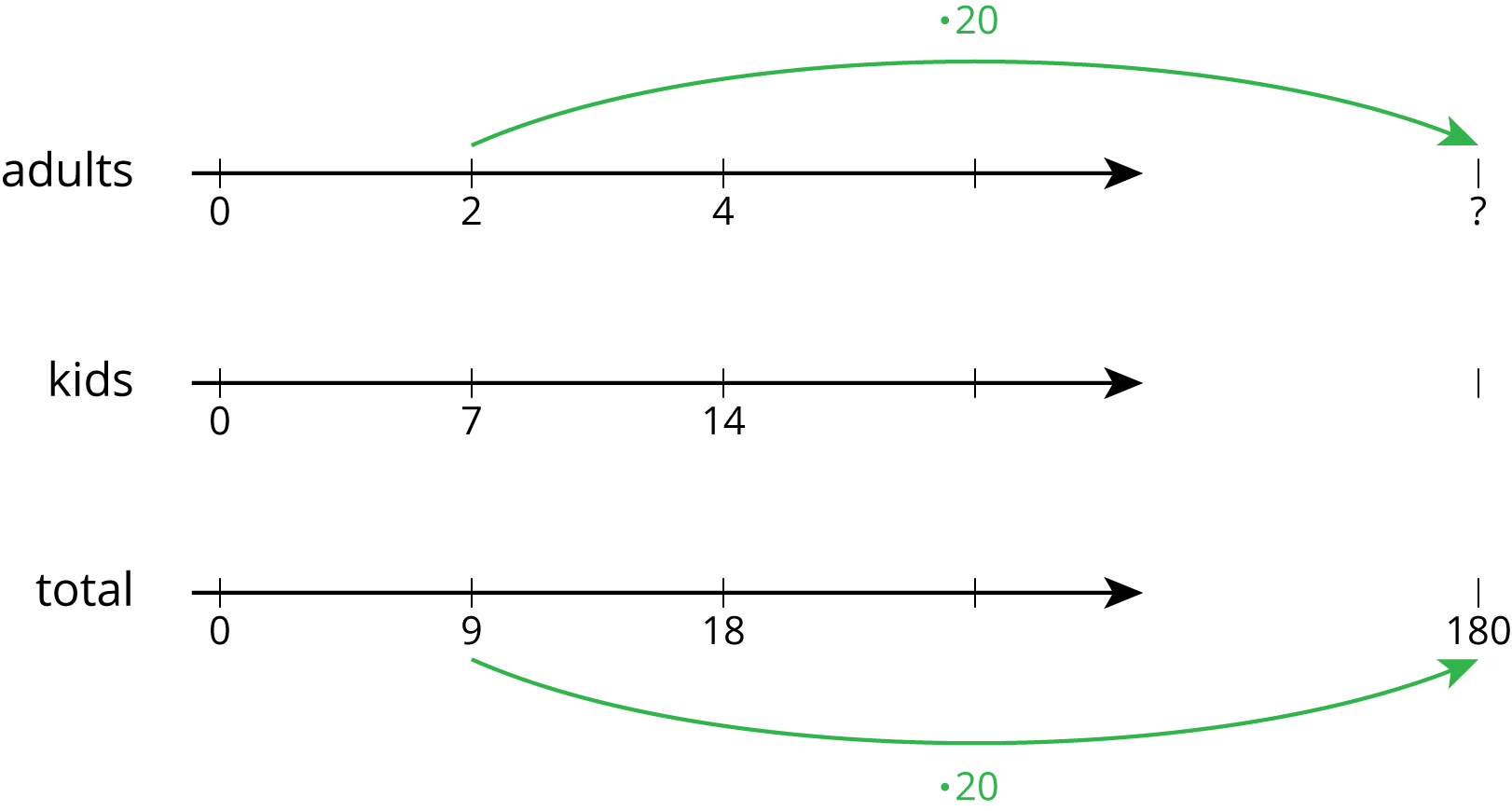
-
Tables are especially useful when the problem has very large or very small numbers.
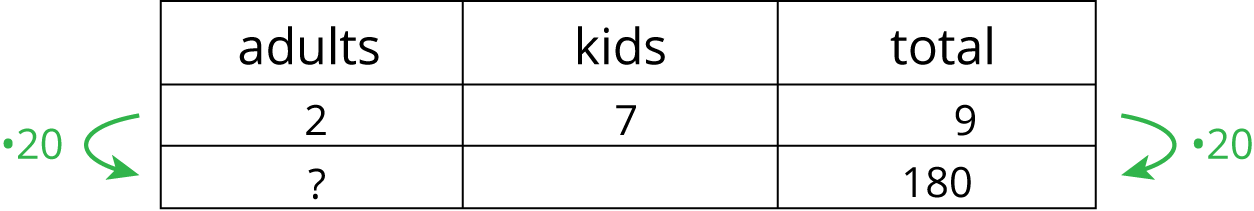
We ask ourselves, “9 times what is 180?” The answer is 20. Next, we multiply 2 by 20 to get the total number of adults in the school.
Another reason to make diagrams is to communicate our thinking to others. Here are some good habits when making diagrams:
- Label each part of the diagram with what it represents.
- Label important amounts.
- Make sure you read what the question is asking and answer it.
- Make sure you make the answer easy to find.
- Include units in your answer. For example, write “4 cups” instead of just “4.”
-
Double check that your ratio language is correct and matches your diagram.