Lesson 6
Introducing Double Number Line Diagrams
6.1: Number Talk: Adjusting Another Factor (10 minutes)
Warm-up
This Number Talk encourages students to think about the numbers in computation problems and rely on what they know about structure, patterns, whole-number multiplication, and properties of operations to mentally solve a problem.
While many strategies may emerge, the focus of this string of problems is for students to see how adjusting a factor impacts the product, and how this insight can be used to reason about other problems. Four problems are given, however, given limited time, it may not be possible to share every strategy. Consider gathering only two or three different strategies per problem. Each problem was chosen to elicit slightly different reasoning, so as students explain their strategies, ask how the factors impacted their product.
Launch
Display one problem at a time. Give students 1 minute of quiet think time per problem and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find the value of each product mentally.
\((4.5)\boldcdot 4\)
\((4.5)\boldcdot 8\)
\(\frac{1} {10}\boldcdot 65\)
\(\frac{2} {10}\boldcdot 65\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see. Ask students if or how the factors in the problem impacted the strategy choice. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone solve the problem the same way but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
Design Principle(s): Optimize output (for explanation)
6.2: Drink Mix on a Double Number Line (15 minutes)
Activity
In this activity, a double number line, a new representation, is presented and interpreted alongside the more familiar discrete diagrams and in the familiar context of recipes.
Students learn that, just like discrete diagrams, double number lines represent equivalent ratios. They see that alignment between the numbers of the two lines matters; that it is through the alignment that the association of two quantities are shown. Students notice pairs of numbers that “line up” vertically are equivalent ratios.
Because double number lines are quicker to draw and can be extended easily to show many more equivalent ratios, they are more efficient than discrete diagrams, especially for dealing with larger quantities.
As students work, monitor for those who contrast the two representations in terms of using graphic symbols versus numbers, and those who think about equivalent ratios in terms of the alignment of numbers in the double number line diagram.
Launch
Ask students to recall the mixture of powdered drink mix and water from a previous lesson. Ask: “How much drink mix and water was in one batch?” (4 teaspoons of drink mix and 1 cup of water.) “What would you need to mix a double batch?” (8 teaspoons of drink mix and 2 cups of water.) Explain that they are going to show batches of a mixture using a double number line diagram.
Give students 5 minutes of quiet think time to make sense of the new representation and answer the questions, followed by time to share their response with a partner and a whole-class discussion afterwards.
Supports accessibility for: Language; Social-emotional skills
Design Principle(s): Support sense-making; Optimize output (for explanation)
Student Facing
The other day, we made drink mixtures by mixing 4 teaspoons of powdered drink mix for every cup of water. Here are two ways to represent multiple batches of this recipe:
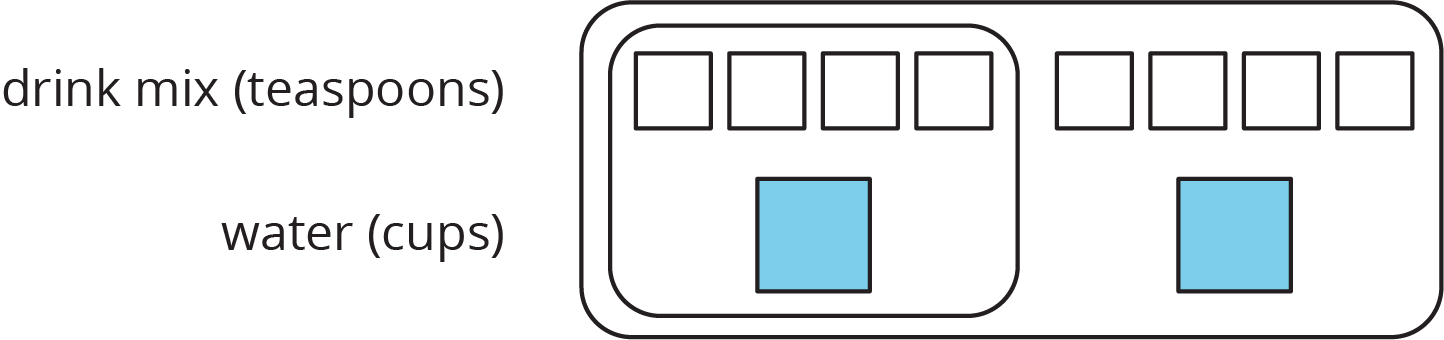
- How can we tell that \(4:1\) and \(12:3\) are equivalent ratios?
- How are these representations the same? How are these representations different?
- How many teaspoons of drink mix should be used with 3 cups of water?
- How many cups of water should be used with 16 teaspoons of drink mix?
- What numbers should go in the empty boxes on the double number line diagram? What do these numbers mean?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Recall that a perfect square is a number of objects that can be arranged into a square. For example, 9 is a perfect square because 9 objects can be arranged into 3 rows of 3. 16 is also a perfect square, because 16 objects can be arranged into 4 rows of 4. In contrast, 12 is not a perfect square because you can’t arrange 12 objects into a square.
- How many whole numbers starting with 1 and ending with 100 are perfect squares?
- What about whole numbers starting with 1 and ending with 1,000?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
While the double number line diagram is given here, some students may not feel comfortable with seeing the same numbers (the 4’s) in different positions. Remind students that each number line represents a different quantity, and that the two 4’s have different meanings.
Activity Synthesis
Select students to share their observations about how the two representations are alike and how they differ. As students discuss solutions to the questions, circle pairs of associated quantities on the double number line. Help students connect information as it is represented in the different diagrams.
On the last question, ask students how they knew that 20 was the next number on the line representing teaspoons of drink mix? (Skip counting by 4; multiply the next number of cups of water by 4.)
Ask students to think more generally for a minute about the representations at hand:
- What is a double number line diagram? What do they do? What do the numbers on the tick marks represent and how should they be scaled?
- What might be some benefits of using double number lines instead of diagrams? (We can use them to show many more batches; they are quicker to draw.)
6.3: Blue Paint on a Double Number Line (15 minutes)
Activity
The purpose of this activity is for students to practice labeling the tick marks on a double number line diagram with equivalent ratios. This activity revisits a familiar context from a previous lesson so students can apply reasoning about different sized batches of a recipe to help them understand the more abstract representation of a double number line diagram.
Some students may interpret the diagram as showing 3 tablespoons of blue paint for every 1 cup of white paint and may choose to label the top line of the double number line diagram counting by 1s instead of 2s and the bottom line counting by 3s instead of 6s. This is also an acceptable correct answer. There are two reasons to monitor for students using this alternate representation. First, when students are comparing their diagrams with their partner if one partner counter by 2s and the other partner counted by 1s, they may need guidance in determining that these are both correct answers. Second, during the whole-class discussion, consider selecting a student with the less common representation to share their solution at the end.
Launch
Give students 4 minutes of quiet work time, followed by time to share their response with a partner and then a whole-class discussion afterwards.
Student Facing
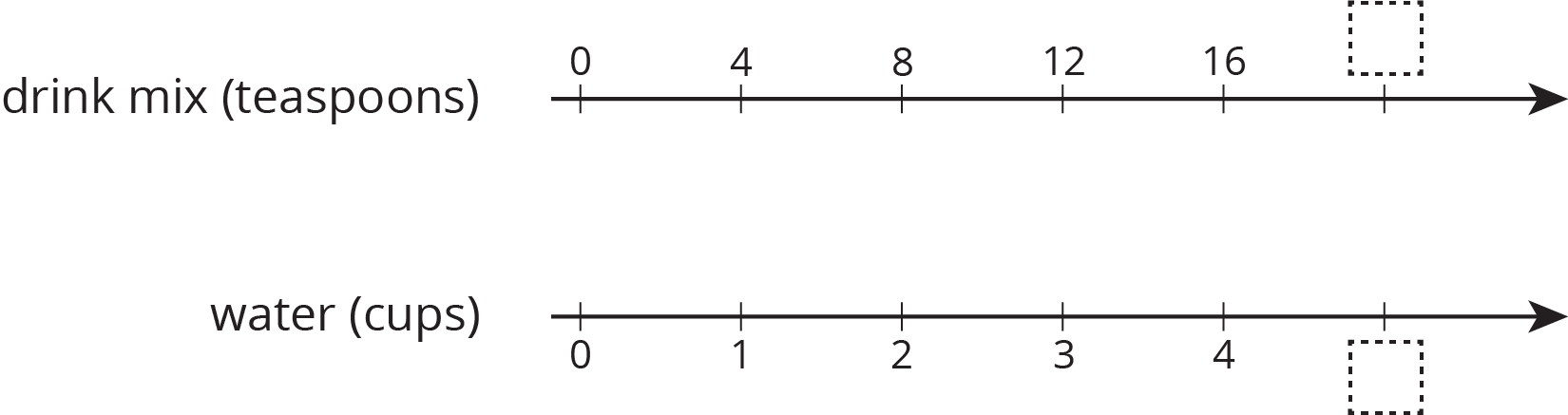
Here is a diagram showing Elena’s recipe for light blue paint.

-
Complete the double number line diagram to show the amounts of white paint and blue paint in different-sized batches of light blue paint.
- Compare your double number line diagram with your partner. Discuss your thinking. If needed, revise your diagram.
- How many cups of white paint should Elena mix with 12 tablespoons of blue paint? How many batches would this make?
- How many tablespoons of blue paint should Elena mix with 6 cups of white paint? How many batches would this make?
- Use your double number line diagram to find another amount of white paint and blue paint that would make the same shade of light blue paint.
- How do you know that these mixtures would make the same shade of light blue paint?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to present their solutions. Help them connect the different ways in which the information is represented in the different diagrams. Emphasize the importance of labeling everything clearly so the interpretation is easy to make.
Design Principle(s): Optimize output (for justification); Cultivate conversation
Lesson Synthesis
Lesson Synthesis
The main ideas to draw out of this lesson are the reasons for using a double number line diagram.
- Double number lines easily display equivalent ratios, with the numbers in each equivalent ratio lining up vertically.
- A double number line diagram can be used when a discrete diagram would be cumbersome or even impossible.
The other major goal of this lesson is building up students’ fluency in creating double number lines. Students will have further opportunities in upcoming lessons, but watch for common errors such as inconsistent labeling and failing to align the equivalent ratios.
6.4: Cool-down - Batches of Cookies on a Double Number Line (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
You can use a double number line diagram to find many equivalent ratios. For example, a recipe for fizzy juice says, “Mix 5 cups of cranberry juice with 2 cups of soda water.” The ratio of cranberry juice to soda water is \(5:2\). Multiplying both ingredients by the same number creates equivalent ratios.
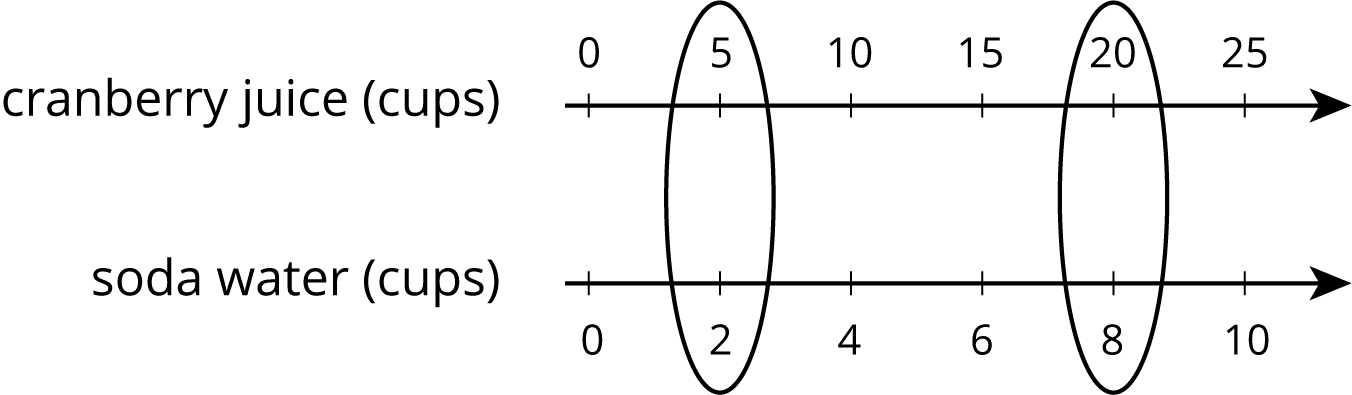
This double number line shows that the ratio \(20:8\) is equivalent to \(5:2\). If you mix 20 cups of cranberry juice with 8 cups of soda water, it makes 4 times as much fizzy juice that tastes the same as the original recipe.