Lesson 9
Constant Speed
Let’s use ratios to work with how fast things move.
9.1: Number Talk: Dividing by Powers of 10
Find the quotient mentally.
\(30\div 10\)
\(34\div 10\)
\(3.4\div 10\)
\(34\div 100\)
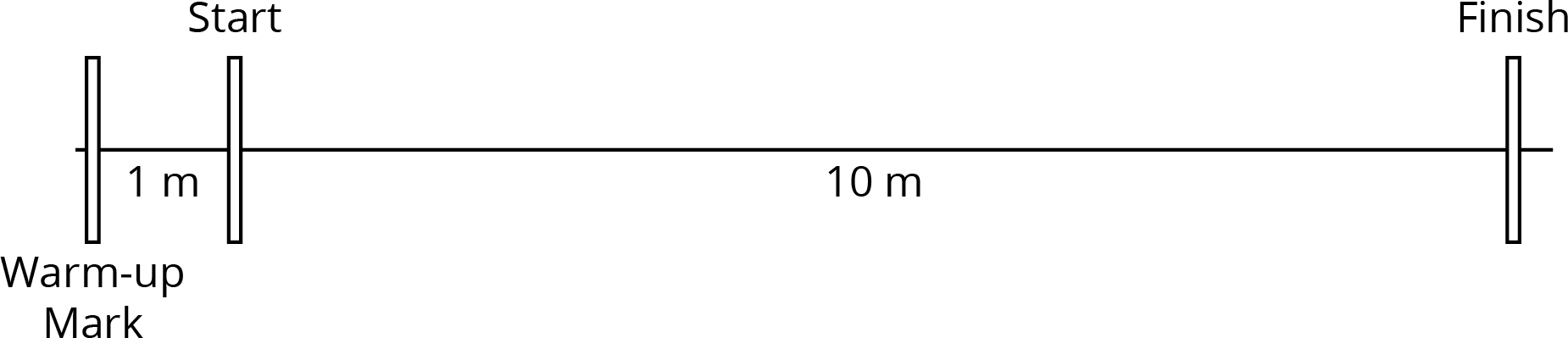
9.2: Moving 10 Meters
Your teacher will set up a straight path with a 1-meter warm-up zone and a 10-meter measuring zone. Follow the following instructions to collect the data.
-
- The person with the stopwatch (the “timer”) stands at the finish line. The person being timed (the “mover”) stands at the warm-up line.
- On the first round, the mover starts moving at a slow, steady speed along the path. When the mover reaches the start line, they say, “Start!” and the timer starts the stopwatch.
- The mover keeps moving steadily along the path. When they reach the finish line, the timer stops the stopwatch and records the time, rounded to the nearest second, in the table.
- On the second round, the mover follows the same instructions, but this time, moving at a quick, steady speed. The timer records the time the same way.
- Repeat these steps until each person in the group has gone twice: once at a slow, steady speed, and once at a quick, steady speed.
your slow moving time (seconds) your fast moving time (seconds)
-
After you finish collecting the data, use the double number line diagrams to answer the questions. Use the times your partner collected while you were moving.
Moving slowly:

Moving quickly:

- Estimate the distance in meters you traveled in 1 second when moving slowly.
- Estimate the distance in meters you traveled in 1 second when moving quickly.
- Trade diagrams with someone who is not your partner. How is the diagram representing someone moving slowly different from the diagram representing someone moving quickly?
9.3: Moving for 10 Seconds
Lin and Diego both ran for 10 seconds, each at a constant speed. Lin ran 40 meters and Diego ran 55 meters.
- Who was moving faster? Explain your reasoning.
- How far did each person move in 1 second? If you get stuck, consider drawing double number line diagrams to represent the situations.
- Use your data from the previous activity to find how far you could travel in 10 seconds at your quicker speed.
- Han ran 100 meters in 20 seconds at a constant speed. Is this speed faster, slower, or the same as Lin’s? Diego’s? Yours?
Lin and Diego want to run a race in which they will both finish when the timer reads exactly 30 seconds. Who should get a head start, and how long should the head start be?
Summary
Suppose a train traveled 100 meters in 5 seconds at a constant speed. To find its speed in meters per second, we can create a double number line:
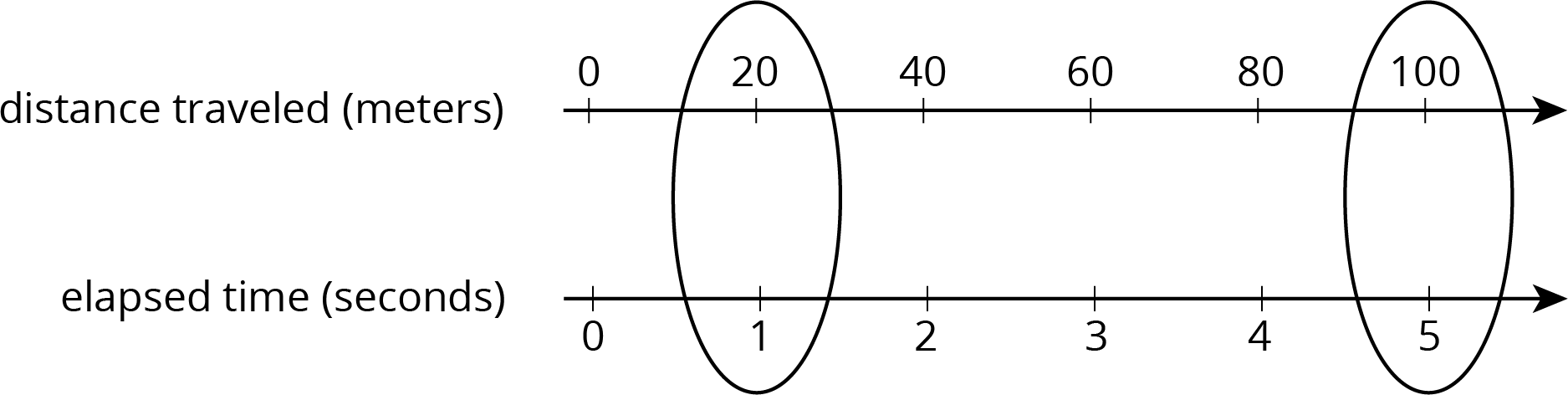
The double number line shows that the train’s speed was 20 meters per second. We can also find the speed by dividing: \(100 \div 5 = 20\).
Once we know the speed in meters per second, many questions about the situation become simpler to answer because we can multiply the amount of time an object travels by the speed to get the distance. For example, at this rate, how far would the train go in 30 seconds? Since \(20 \boldcdot 30 = 600\), the train would go 600 meters in 30 seconds.
Glossary Entries
- double number line diagram
A double number line diagram uses a pair of parallel number lines to represent equivalent ratios. The locations of the tick marks match on both number lines. The tick marks labeled 0 line up, but the other numbers are usually different.
- meters per second
Meters per second is a unit for measuring speed. It tells how many meters an object goes in one second.
For example, a person walking 3 meters per second is going faster than another person walking 2 meters per second.
- per
The word per means “for each.” For example, if the price is $5 per ticket, that means you will pay $5 for each ticket. Buying 4 tickets would cost $20, because \(4 \boldcdot 5 = 20\).
- unit price
The unit price is the cost for one item or for one unit of measure. For example, if 10 feet of chain link fencing cost $150, then the unit price is \(150 \div 10\), or $15 per foot.