Lesson 1
Introducing Ratios and Ratio Language
1.1: What Kind and How Many? (5 minutes)
Warm-up
In this warm-up, students compare figures and sort them into categories.
Launch
Display the image for all to see. Give students 1 minute of quiet think time followed by 2 minutes of partner discussion.
Student Facing
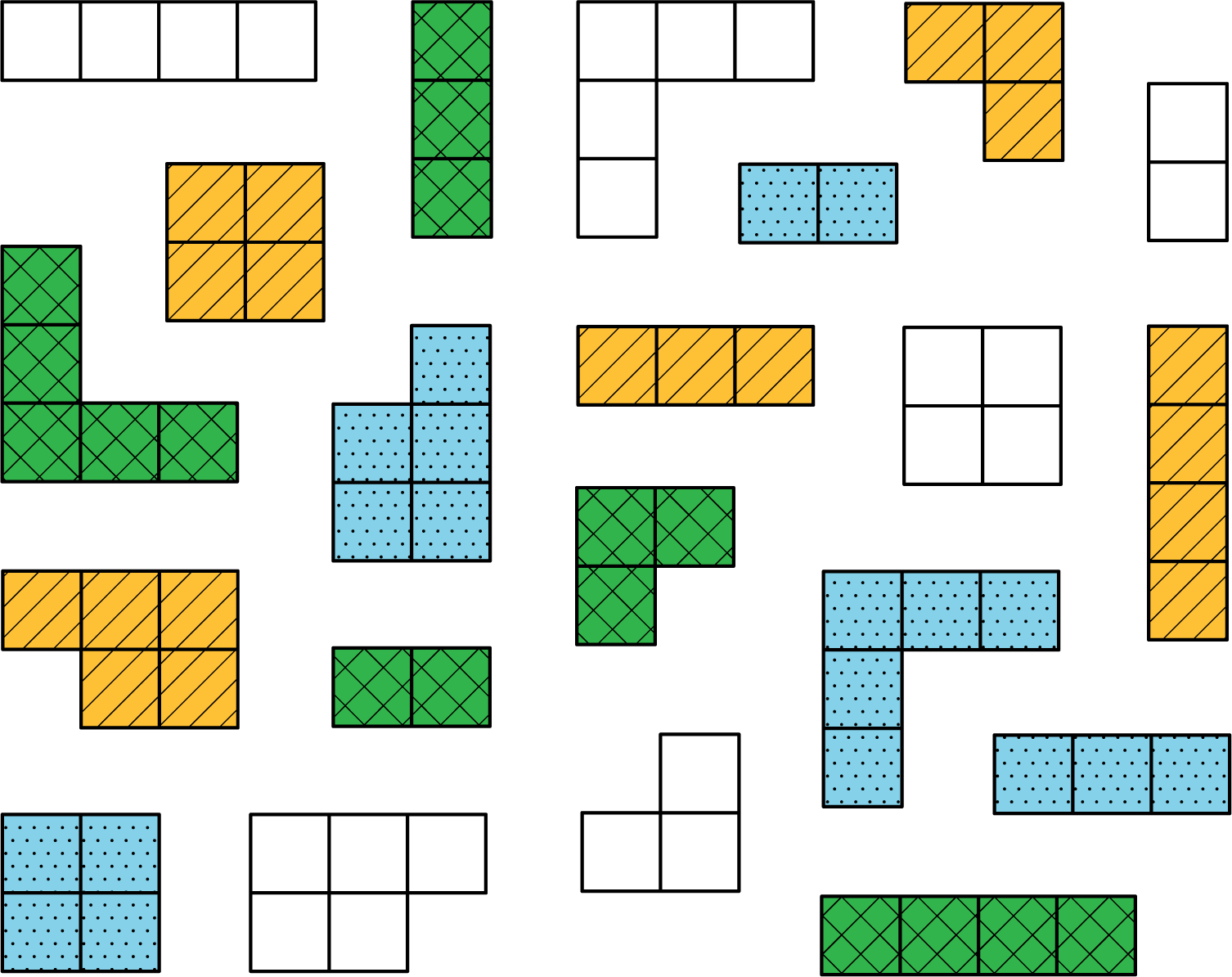
Think of different ways you could sort these figures. What categories could you use? How many groups would you have?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to create their own categories, prompt them to consider a specific attribute of the figures, such as the size, color, or shape.
Activity Synthesis
Record all the ways students answered the question for all to see. Ask a student to explain how they sorted the figures. Ask if anyone saw it a different way until all the different ways of seeing the shapes have been shared. Emphasize that the important thing is to describe the way they sorted them clearly enough that everyone agrees that it is a reasonable way to sort them. Tell students we will be looking at different ways of seeing the same set of objects in the next activity.
1.2: The Teacher’s Collection (10 minutes)
Activity
This activity introduces students to ratio language and notation through examples based on a collection of everyday objects. Students learn that a ratio is an association between quantities, and that this association can be expressed in multiple ways.
After discussing examples of ratio language and notation for one way of categorizing the objects in the collection, students write ratios to describe the quantities for another way of categorizing objects in the collection.
As students work, circulate and identify those who:
- Create different categories from the given collection.
- Create categories whose quantities can be rearranged into smaller groups (e.g. 6 A’s and 4 B’s can be expressed as “for every 3 A’s there are 2 B’s”).
- Express the same ratio in opposite order or by using different words (e.g. “the ratio of A to B is 7 to 3,” and “for every 7 A’s there are 3 B’s”).
Have a collection of objects ready to display for the launch. Make sure there are different ways the collection can be sorted. For example, the dinosaurs below can be categorized by color (green, orange, and purple), by the number of legs they stand on (standing on 4 legs or on 2 legs), or by the features along their backs (crest, white stripe, or nothing).

Familiar classroom objects such as binder clips or pattern blocks can also be used to form collections. This picture shows a collection of binder clips that could be categorized by size (small, medium, and large) or by color (black, green, and blue) .

Launch
Display a collection of objects for all to see. Give students 2 minutes of quiet think time to come up with as many different categories for sorting the collection as they can think of. Record students’ categories for all to see. Sort the collection into one of the student-suggested categories and count the number of items in each. Record the number of objects in each category and display for all to see. For example:
| category A: green | category B: orange | category C: purple |
|---|---|---|
| 3 | 2 | 4 |
Explain that we can talk about the quantities in the different categories using something called ratios. Tell students: “A ratio is an association between two or more quantities.” We use a colon, or the word “to,” between two values we are associating.
Share the following examples (adapt them to suit your collection) and display them for all to see. Keep the examples visible for the duration of the lesson.
- The ratio of purple to orange dinosaurs is 4 to 2.
- The ratio of purple to orange dinosaurs is \(4:2\).
- The ratio of orange to purple dinosaurs is 2 to 4.
- The ratio of orange to purple dinosaurs is \(2:4\)
Explain that we can also associate two quantities using the phrase “for every \(a\) of these, there are \(b\) of those.” Add the following examples to the display.
- For every 3 green dinosaurs there are 4 purple dinosaurs.
- There are 4 purple dinosaurs for every 2 orange dinosaurs.
Finally, find two categories whose items can be rearranged into smaller groups, e.g. 4 purple dinosaurs to 2 orange dinosaurs. Point out that in some cases we can associate the same categories using different numbers. Share the following example and add it to the display.
- For every 2 purple dinosaurs, there is 1 orange dinosaur.

Have students write two or three sentences to describe ratios between the categories they suggested.
Supports accessibility for: Conceptual processing; Language
Student Facing
-
Think of a way to sort your teacher’s collection into two or three categories. Count the items in each category, and record the information in the table.
category name category amount Pause here so your teacher can review your work.
-
Write at least two sentences that describe ratios in the collection. Remember, there are many ways to write a ratio:
-
The ratio of one category to another category is ________ to ________.
-
The ratio of one category to another category is ________ : ________.
-
There are _______ of one category for every _______ of another category.
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may write ratios with no descriptive words. \(8:2\) is a good start, but part of writing a ratio is stating what those numbers mean. Draw students’ attention to the sentence stems in the task statement; encourage them to use those words.
Activity Synthesis
Invite several students to share their categories and sentences. Display them for all to see, attending to correct ratio language. Be sure to include students who express the same categories in reverse order, in different words, or with a different set of numbers (which students will later call an equivalent ratio). Leave several sentences displayed for students to see and use as a reference while working on the next task.
1.3: The Student’s Collection (20 minutes)
Activity
In this activity, students write ratios to describe objects in their own collection. They create a display of objects and circulate to look at their classmates’ work. Students see that there are several ways to write ratios to describe the same situation.
Launch
Invite students to share what types of items are in their personal collections. If students did not bring in a collection, pair them with another student, or provide them with an extra collection that you have brought in for that purpose.
Provide access to tools for creating a visual display. Tell students they will pause their work before creating a visual display to get their sentences approved.
Design Principle(s): Maximize meta-awareness; Optimize output
Student Facing
-
Sort your collection into three categories. You can experiment with different ways of arranging these categories. Then, count the items in each category, and record the information in the table.
category name category amount -
Write at least two sentences that describe ratios in the collection. Remember, there are many ways to write a ratio:
- The ratio of one category to another category is ________ to ________.
- The ratio of one category to another category is ________ : ________.
-
There are _______ of one category for every _______ of another category.
Pause here so your teacher can review your sentences.
- Make a visual display of your items that clearly shows one of your statements. Be prepared to share your display with the class.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- Use two colors to shade the rectangle so there are 2 square units of one color for every 1 square unit of the other color.
-
The rectangle you just colored has an area of 24 square units. Draw a different shape that does not have an area of 24 square units, but that can also be shaded with two colors in a \(2:1\) ratio. Shade your new shape using two colors.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Watch for students simply writing a numerical ratio, such as \(3:7\), without any descriptive words. Draw their attention to the sentence stems in the task statement.
Activity Synthesis
Once students have had enough time to create their displays, circulate through each display and listen to how students describe their ratios.
As students present their displays, point out the various ways that students chose to showcase their work, including different ways to say the same ratio. Ask students who used two sets of numbers to describe the same categories (e.g., 8 to 2 and “4 for every 1”) to demonstrate the two ways of grouping the objects.
Lesson Synthesis
Lesson Synthesis
This lesson is all about how to use ratio language and notation to describe an association between two or more quantities. Wrap up the lesson by drawing a diagram for all to see of, say, 6 squares and 3 circles.

Say, “One way to write this ratio is, there are 6 squares for every 3 circles. What are some other ways to write this ratio?” Some correct options might be:
- The ratio of squares to circles is \(6:3\).
- The ratio of circles to squares is 3 to 6.
- There are 2 squares for every 1 circle.
Display this diagram and the associated sentences the class comes up with somewhere in the classroom so students can refer back to the correct ratio and rate language during subsequent lessons.
Consider posing some more general questions, such as:
- Explain what a ratio is in your own words.
- What things must you pay attention to when writing a ratio?
- What are some words and phrases that are used to write a ratio?
1.4: Cool-down - A Collection of Animals (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A ratio is an association between two or more quantities. There are many ways to describe a situation in terms of ratios. For example, look at this collection:

Here are some correct ways to describe the collection:
- The ratio of squares to circles is \(6:3\).
- The ratio of circles to squares is 3 to 6.
Notice that the shapes can be arranged in equal groups, which allow us to describe the shapes using other numbers.

- There are 2 squares for every 1 circle.
- There is 1 circle for every 2 squares.