Lesson 7
Creating Double Number Line Diagrams
7.1: Ordering on a Number Line (10 minutes)
Warm-up
In this warm-up, students partition a number line and locate fraction and decimal equivalents in preparation for working with double number lines in this unit. Students are purposely not asked to locate 1 on the number line to see how they reason about locating the \(\frac12\) and \(\frac14\). It is important for students to be able to identify the fractions or decimals and label tick marks correctly, interpreting the distance between tick marks, rather than the number of tick marks, as the fractional size. As students discuss with their partner, select students to share their answers to the first question during the whole-class discussion.
Launch
Arrange students in groups of 2. Display the number line for all to see. Give students 2 minutes of quiet think time and ask them to give a signal when they have an answer and a strategy. Ask students to compare their number line with a partner and share the fractions or decimals they chose to place on the number line for the second question.
Design Principle(s): Support sense-making
Student Facing
-
Locate and label the following numbers on the number line:
\(\frac12\)
\(\frac14\)
\(1\frac34\)
1.5
1.75
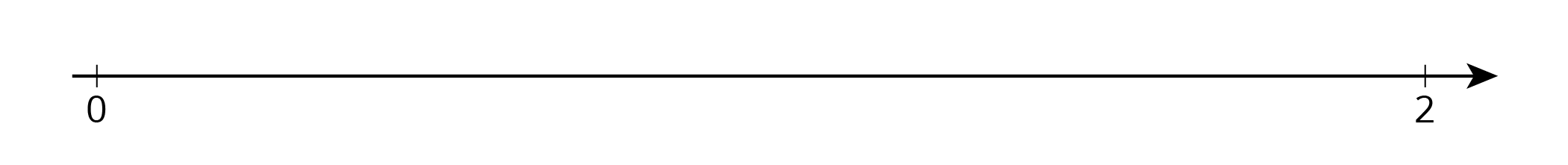
- Based on where you placed the numbers, locate and label four more fractions or decimals on the number line.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may place \(\frac12\) in the center of the number line, reasoning that it is half of the number line. Explain to the students they are placing the number \(\frac12\), which has a specific value and location on the number line.
Activity Synthesis
Select students to explain how they reasoned about the location of each number on the number line. After each number, ask the class whether they agree or disagree, and if anyone else had a different way of thinking about that number. If time permits, ask students to share the fractions or decimals they located for the second question. Discuss why they chose those numbers and how they decided on their location.
7.2: Just a Little Green (10 minutes)
Activity
Students continue to use double number lines to reason about equivalent ratios. Here students’ attention is directed to the \(1:3\) blue-to-yellow ratio in the green water recipe, which can then be used to determine any equivalent ratio. The task is also the beginning of students’ exploration of finding and using ratios containing a 1.
One key idea to convey here is that finding a ratio associated with 1 unit of a quantity can be very helpful. Another is that the intervals on double number lines can be subdivided to help us find such ratios.
As students work, identify those who use division to determine the \(1:3\) ratio, and then use multiplication to determine the ratios for 8 ml and 13 ml of blue water. This is a key insight for a type of reasoning that is broadly useful and will be developed further.
Launch
Ask students to recall what double number lines are and how they can be used to represent problems involving equivalent ratios. Explain that they are going to investigate the structure of double number lines in more detail. Give students 5 minutes of quiet think time, and then time to discuss their responses with a partner.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Design Principle(s): Optimize output (for generalization)
Student Facing
The other day, we made green water by mixing 5 ml of blue water with 15 ml of yellow water. We want to make a very small batch of the same shade of green water. We need to know how much yellow water to mix with only 1 ml of blue water.
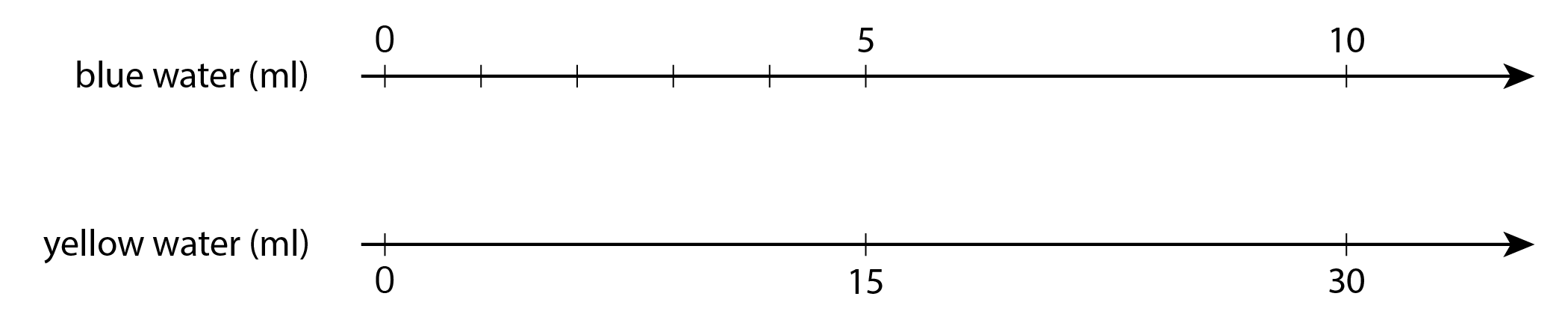
- On the number line for blue water, label the four tick marks shown.
- On the number line for yellow water, draw and label tick marks to show the amount of yellow water needed for each amount of blue water.
- How much yellow water should be used for 1 ml of blue water? Circle where you can see this on the double number line.
- How much yellow water should be used for 11 ml of blue water?
- How much yellow water should be used for 8 ml of blue water?
- Why is it useful to know how much yellow water should be used with 1 ml of blue water?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may have trouble figuring out that the length of a segment between consecutive tick marks is \(\frac15\) of the interval from 0 to 5, especially since there are four tick marks (not five). When focusing on blue, students’ first guess about the tick marks is generally correct. For yellow, remind them that the numbers on the tick marks are made by skip counting; they are then likely to try 3’s and 5’s since both can make 15. Students who label the spaces between tick marks rather than the tick marks themselves may need additional work with important measurement conventions.
Activity Synthesis
Debrief as a class after students have a chance to share their work with a partner. Focus discussions on how students determine the amount of yellow water for 1 ml of blue, and how they determine the amounts of yellow for 8 ml and 11 ml of blue. Select students who used division (to find the former) and multiplication (to find the latter) to share.
If students do not do so, frame the relationship of blue to yellow using phrases such as “for every 1 ml of . . . ” or “per milliliter of . . .”
- “There are 3 milliliters of yellow water for every 1 milliliter of blue water.”
- “There are 3 milliliters of yellow water per milliliter of blue water.”
The word per means “for every.” Ask students to think of any other situation in which they may use the word “per” as it is used here (e.g., price per bottle of water, cost per ticket, etc.) and discuss why knowing the value of one item would be helpful.
7.3: Art Paste on a Double Number Line (20 minutes)
Activity
In the previous lesson, students were given blank double number line diagrams and were only responsible for labeling them to match the situation. In this activity, students draw their own double number line diagram from scratch and identify which elements are important to create a useful double number line diagram.
Launch
“You just used a double number line to solve some problems. Now, you’ll create a double number line from scratch. Once you know how to make double number lines, you can use them for any situation with equivalent ratios.”
Arrange students in groups of 2. Ensure each student has access to a ruler. Have students check with a partner and come to an agreement about how to draw the diagrams before moving on to question 3.
Design Principle(s): Support sense-making
Student Facing
A recipe for art paste says “For every 2 pints of water, mix in 8 cups of flour.”
-
Follow the instructions to draw a double number line diagram representing the recipe for art paste.
- Use a ruler to draw two parallel lines.
- Label the first line “pints of water.” Label the second line “cups of flour.”
- Draw at least 6 equally spaced tick marks that line up on both lines.
- Along the water line, label the tick marks with the amount of water in 0, 1, 2, 3, 4, and 5 batches of art paste.
- Along the flour line, label the tick marks with the amount of flour in 0, 1, 2, 3, 4, and 5 batches of art paste.
-
Compare your double number line diagram with your partner’s. Discuss your thinking. If needed, revise your diagram.
-
Next, use your double number line to answer these questions:
- How much flour should be used with 10 pints of water?
- How much water should be used with 24 cups of flour?
- How much flour per pint of water does this recipe use?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A square with side of 10 units overlaps a square with side of 8 units in such a way that its corner \(B\) is placed exactly at the center of the smaller square. As a result of the overlapping, the two sides of the large square intersect the two sides of the small square exactly at points \(C\) and \(E\), as shown. The length of \(CD\) is 6 units.

What is the area of the overlapping region \(CDEB\)?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not label tick marks with equal increments or may not align the tick marks.
Activity Synthesis
Select students to explain how they used their double number line diagram to answer the last question. Ask students how they can indicate the number of cups of flour per pint of water on the double number line.
If desired, capitalize on ways students might have incorrectly constructed their double number line. For example:
- Do all increments on each line need to be equal? Why or why not?
- Do the tick marks on the top line need to match those on the bottom line? Why/why not?
- Does it matter what number we use to start each line? Why or why not?
7.4: Revisiting Tuna Casserole (10 minutes)
Optional activity
In this activity, students revisit familiar contexts they represented with discrete diagrams in previous lessons. Here, they see how double number line diagrams are helpful for answering more questions about these situations.
Monitor for students who use a discrete diagram and for students who use a double number line diagram.
Launch
Arrange students in groups of 2.
Student Facing
The other day, we looked at a recipe for tuna casserole that called for 10 ounces of cream of chicken soup for every 3 cups of elbow-shaped pasta.
- Draw a double number line diagram that represents the amounts of soup and pasta in different-sized batches of this recipe.
- If you made a large amount of tuna casserole by mixing 40 ounces of soup with 15 cups of pasta, would it taste the same as the original recipe? Explain or show your reasoning.
- The original recipe called for 6 ounces of tuna for every 3 cups of pasta. Add a line to your diagram to represent the amount of tuna in different batches of casserole.
- How many ounces of soup should you mix with 30 ounces of tuna to make a casserole that tastes the same as the original recipe?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to present their solutions. Sequence discrete diagrams first and double number line diagrams second. Help students see connections between the two representations.
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Create a double number line with the help of the class. Start by asking, "What are some important things to pay attention to when you create a double number line?" Then, "What situation should we represent?" It is fine to choose a situation that students have already encountered in this lesson or an earlier lesson.
As you are creating the double number line together, write down anything mentioned that it is important to pay attention to. For example:
- The two lines you draw should be parallel to each other. One practice is to use both edges of a ruler to create two parallel lines. But double number lines are tools for reasoning, so they don't have to be perfect.
- Each line should be labeled with what it represents. Include units of measure.
- Tick marks should be evenly spaced, and the two sets of tick marks should be lined up vertically in pairs.
One strategy might be to intentionally do something wrong, and ask students how you should fix it. For example, draw tick marks that are very obviously not evenly spaced, or neglect to include units of measure in your labels.
7.5: Cool-down - Revisiting Paws, Ears, and Tails (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here are some guidelines to keep in mind when drawing a double number line diagram:
- The two parallel lines should have labels that describe what the numbers represent.
- The tick marks and numbers should be spaced at equal intervals.
- Numbers that line up vertically make equivalent ratios.
For example, the ratio of the number of eggs to cups of milk in a recipe is \(4:1\). Here is a double number line that represents the situation:
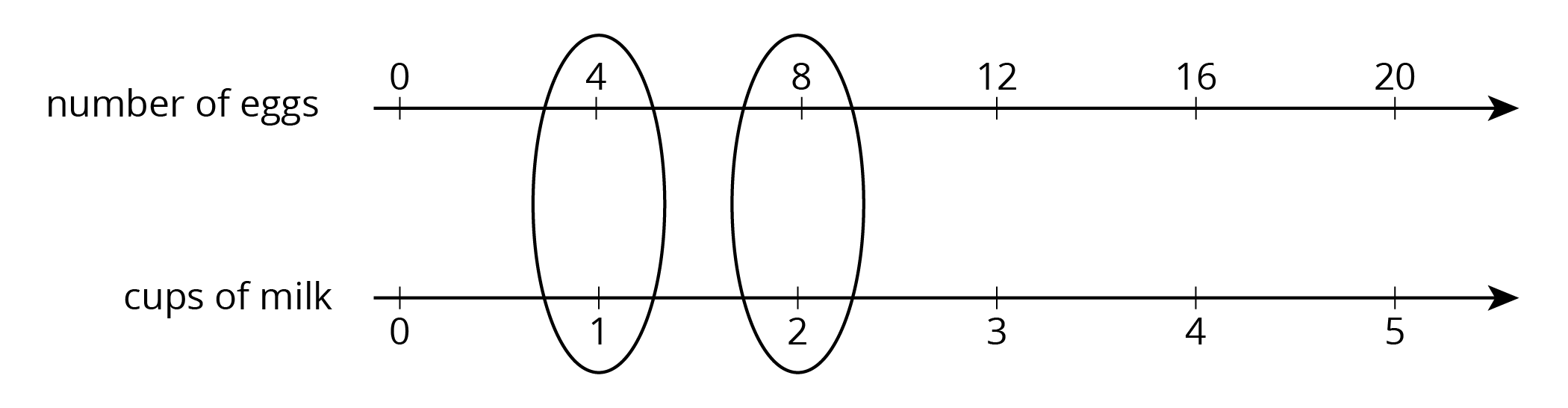
We can also say that this recipe uses “4 eggs per cup of milk” because the word per means “for each.”