Lesson 8
How Much for One?
8.1: Number Talk: Remainders in Division (10 minutes)
Warm-up
This number talk encourages students to think about the numbers in a computation problem and rely on what they know about structure, patterns, and division with remainders to mentally solve a problem.
Only one problem is presented to allow students to share a variety of strategies for division. Notice how students handle a remainder in a problem, which may depend on their prior experiences with division. Students may write it as “r_” and struggle with either fraction or decimal notation. In the next lesson, when students begin finding unit price, they will need to be able to interpret the remainder in either decimal or fraction form.
Launch
Display the problem for all to see. Give students 2 minutes of quiet think time and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find the quotient mentally.
\(246\div 12\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle to interpret the remainder as a decimal or fraction and may instead write r 6.
Activity Synthesis
Invite students to share their strategies. Record and display student explanations for all to see. Ask students to explain if or how the dividend or divisor impacted their choice of strategy and how they decided to write their remainder. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone solve the problem the same way but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
At the end of discussion, if time permits, ask a few students to share a story problem or context that \(246\div 12 = 20.5\) would represent.
Design Principle(s): Optimize output (for explanation)
8.2: Grocery Shopping (10 minutes)
Activity
This activity continues the work on ratios involving one unit of something. Students determine the prices of grocery items and learn to use the term unit price to describe cost per unit. To determine unit prices, students may:
- Divide the cost by the number of items
- Use discrete diagrams
- Use a double number line
As students work, monitor for students using different methods.
If students choose to draw a double number line diagram, remind them to label each number line and to circle the ratio where they find the answer.
Launch
Frame the task in shopping terms. Say that when most of us go shopping, we often see prices for multiple items or units (e.g., 2 bottles for $3, or $1.99 for three pounds, etc.). But sometimes we want to know how much it costs to buy just one item or one unit of something. Tell students they will explore the use of “per” in the context of shopping. Ask students to solve the problems involving “price for one” using any method, and to be ready to explain their reasoning. Provide access to rulers in case students choose to draw double number lines. Give students a few minutes of quiet think time. Pause after the first question, and if any students say the answer is 2, point out that is dollars per avocado rather than avocados per dollar.
If students have digital access, they can use an applet to explore the problem and justify their reasoning before discussing with a partner. Allow students 1–2 minutes of work time and then demonstrate how to use the applet with the first problem.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Maximize meta-awareness
How It Happens:
-
After students complete the first question, bring the class together and present only the stem:
Twelve large bottles of water cost $9.
Do not allow students to see the follow-up questions for this situation.
Ask students, “What mathematical questions could you ask about this situation?”
-
Give students 1 minute of individual time to jot some notes, and then 3 minutes to share ideas with a partner.
As pairs discuss, support students in using conversation skills to generate and refine their questions collaboratively by seeking clarity, referring to students’ written notes, and revoicing oral responses as necessary. Listen for students’ use of ‘per’ as they talk.
If using the applet, have pairs use the applet together. Check that students correctly identify and enter the quantities (water bottles and dollars) so their sense-making with the tick marks is grounded in a clear enough interpretation of the situation.
-
Ask each pair of students to contribute one written question to a poster, the whiteboard, or digital projection. Call on 2–3 pairs of students to present their question to the whole class, and invite the class to make comparisons among the questions shared and their own questions.
Listen for questions intended to ask about the unit price for a single water bottle, and listen for their use of ‘per’. Revoice student ideas with an emphasis on the use of ‘per’ wherever it serves to clarify a question.
-
Reveal the follow-up questions for this situation and give students a couple of minutes to compare these three questions to their own and those of their classmates. Identify similarities and differences.
- How many bottles can you buy for $3?
- What is the cost per bottle of water?
- How much would 7 bottles of water cost?
Invite students to choose one question to answer (from the class or from the curriculum), and then have students move on to the following problems.
Student Facing
Answer each question and explain or show your reasoning.
-
Eight avocados cost $4.
- How much do 16 avocados cost?
- How much do 20 avocados cost?
- How much do 9 avocados cost?
-
Twelve large bottles of water cost $9.
- How many bottles can you buy for $3?
- What is the cost per bottle of water?
- How much would 7 bottles of water cost?
-
A 10-pound sack of flour costs $8.
- How much does 40 pounds of flour cost?
- What is the cost per pound of flour?
Here is an applet you can use if you choose to.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Frame the task in shopping terms. Say that when most of us go shopping, we often see prices for multiple items or units (e.g., 2 bottles for $3, or $1.99 for three pounds, etc.). But sometimes we want to know how much it costs to buy just one item or one unit of something. Tell students they will explore the use of “per” in the context of shopping. Ask students to solve the problems involving “price for one” using any method, and to be ready to explain their reasoning. Provide access to rulers in case students choose to draw double number lines. Give students a few minutes of quiet think time. Pause after the first question, and if any students say the answer is 2, point out that is avocados per dollar rather than dollars per avocado.
If students have digital access, they can use an applet to explore the problem and justify their reasoning before discussing with a partner. Allow students 1–2 minutes of work time and then demonstrate how to use the applet with the first problem.
Supports accessibility for: Memory; Conceptual processing
Writing and Conversing: Math Language Routine 5 Co-Craft Questions. This is the first time Math Language Routine 5 is suggested as a support in this course. In this routine, students are given a context or situation, often in the form of a problem stem with or without numerical values. Students develop mathematical questions that can be asked about the situation. A typical prompt is: "What mathematical questions could you ask about this situation?" The purpose of this routine is to allow students to make sense of a context before feeling pressure to produce answers, and to develop students’ awareness of the language used in mathematics problems.
Design Principle(s): Maximize meta-awareness
How It Happens:
-
After students complete the first question, bring the class together and present only the stem:
Twelve large bottles of water cost $9.
Do not allow students to see the follow-up questions for this situation.
Ask students, “What mathematical questions could you ask about this situation?”
-
Give students 1 minute of individual time to jot some notes, and then 3 minutes to share ideas with a partner.
As pairs discuss, support students in using conversation skills to generate and refine their questions collaboratively by seeking clarity, referring to students’ written notes, and revoicing oral responses as necessary. Listen for students’ use of ‘per’ as they talk.
If using the applet, have pairs use the applet together. Check that students correctly identify and enter the quantities (water bottles and dollars) so their sense-making with the tick marks is grounded in a clear enough interpretation of the situation.
-
Ask each pair of students to contribute one written question to a poster, the whiteboard, or digital projection. Call on 2–3 pairs of students to present their question to the whole class, and invite the class to make comparisons among the questions shared and their own questions.
Listen for questions intended to ask about the unit price for a single water bottle, and listen for their use of ‘per’. Revoice student ideas with an emphasis on the use of ‘per’ wherever it serves to clarify a question.
-
Reveal the follow-up questions for this situation and give students a couple of minutes to compare these three questions to their own and those of their classmates. Identify similarities and differences.
- How many bottles can you buy for $3?
- What is the cost per bottle of water?
- How much would 7 bottles of water cost?
-
Invite students to choose one question to answer (from the class or from the curriculum), and then have students move on to the following problems.
Student Facing
Answer each question and explain or show your reasoning. If you get stuck, consider drawing a double number line diagram.
-
Eight avocados cost $4.
- How much do 16 avocados cost?
- How much do 20 avocados cost?
- How much do 9 avocados cost?

-
Twelve large bottles of water cost $9.
- How many bottles can you buy for $3?
- What is the cost per bottle of water?
- How much would 7 bottles of water cost?

-
A 10-pound sack of flour costs $8.
- How much does 40 pounds of flour cost?
- What is the cost per pound of flour?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
It is commonly thought that buying larger packages or containers, sometimes called buying in bulk, is a great way to save money. For example, a 6-pack of soda might cost $3 while a 12-pack of the same brand costs $5.
Find 3 different cases where it is not true that buying in bulk saves money. You may use the internet or go to a local grocery store and take photographs of the cases you find. Make sure the products are the same brand. For each example that you find, give the quantity or size of each, and describe how you know that the larger size is not a better deal.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have difficulty with the answers not being integers. Either fractions or decimals are acceptable. Fractions provide the most direct route, but decimals are common for working with dollars and cents. Also, students may use the larger numbers as the dividend, simply because they are larger. Encourage students to check the reasonableness of their answers.
Activity Synthesis
Select students who used unique methods to share their reasoning, as listed in the narrative. If no one used double number lines, represent one of the statements with a double number line diagram and display it for all to see. Although double number lines are not required in the task, their use in the context of problem situations helps students see their merits and illustrates how they might be used in other problems, especially as students transition from unit prices to constant speed and other contexts. Draw connections between the double number line strategy and the dividing by the numbers of items strategy.
Tell students that each “cost per one” unit being sold—avocado, pound, or bottle—is an example of a unit price. Ask them to name as many kinds of unit prices they can and to think of a situation where they might be used, starting with the list from the task:
- Cost per avocado
- Cost per pound
- Cost per bottle
Other possibilities include cost per liter, cost per ounce, cost per jelly bean, and so on.
8.3: More Shopping (15 minutes)
Activity
In this task, students practice finding unit prices, using different reasoning strategies, and articulating their reasoning. They also learn about the term “at this rate.”
As students work, observe their work and then assign one problem for each group to own and present to the class. (The problems can each be assigned to more than one group). Have them work together to create a visual display of their problem and its solution.
Launch
Arrange students in groups of 3–4. Provide tools for creating a visual display and access to rulers. Explain that they will work together to solve some shopping problems, run their work by you, and prepare to present an assigned problem to the class. Tell students that they can use double number lines if they wish.
Display the problem and read it aloud: Pizza costs $1.25 per slice. At this rate, how much will 6 slices cost?
Ask students what they think “at this rate” means in the question. Ensure they understand that “at this rate” means we know that equivalent ratios are involved:
- The ratio of cost to number of slices is $1.25 to 1. That is, pizza costs $1.25 per slice.
- The ratio of cost to number of slices is something to 6. That is, pizza costs something for 6 slices.
The something is the thing we are trying to figure out, and “at this rate” tells us that the two ratios in this situation are equivalent. Another way to understand “at this rate” in this context is “at this price per unit” and that the price per unit is the same no matter how many items or units are purchased.
Discuss any expectations for the group presentation. For example, each group member might be assigned a specific role for the presentation.
If students have digital access, they can use an applet to explore the problems and justify their reasoning before preparing their presentations.
Student Facing
-
Four bags of chips cost $6.
-
What is the cost per bag?
-
At this rate, how much will 7 bags of chips cost?
-
- At a used book sale, 5 books cost $15.
-
What is the cost per book?
-
At this rate, how many books can you buy for $21?
-
- Neon bracelets cost $1 for 4.
-
What is the cost per bracelet?
-
At this rate, how much will 11 neon bracelets cost?
Pause here so your teacher can review your work.
-
- Your teacher will assign you one of the problems. Create a visual display that shows your solution to the problem. Be prepared to share your solution with the class.
Here is an applet you may use if you choose to.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 3–4. Provide tools for creating a visual display and access to rulers. Explain that they will work together to solve some shopping problems, run their work by you, and prepare to present an assigned problem to the class. Tell students that they can use double number lines if they wish.
Display the problem and read it aloud: Pizza costs $1.25 per slice. At this rate, how much will 6 slices cost?
Ask students what they think “at this rate” means in the question. Ensure they understand that “at this rate” means we know that equivalent ratios are involved:
- The ratio of cost to number of slices is $1.25 to 1. That is, pizza costs $1.25 per slice.
- The ratio of cost to number of slices is something to 6. That is, pizza costs something for 6 slices.
The something is the thing we are trying to figure out, and “at this rate” tells us that the two ratios in this situation are equivalent. Another way to understand “at this rate” in this context is “at this price per unit” and that the price per unit is the same no matter how many items or units are purchased.
Discuss any expectations for the group presentation. For example, each group member might be assigned a specific role for the presentation.
If students have digital access, they can use an applet to explore the problems and justify their reasoning before preparing their presentations.
Student Facing
-
Four bags of chips cost $6.
- What is the cost per bag?
- At this rate, how much will 7 bags of chips cost?
-
At a used book sale, 5 books cost $15.
- What is the cost per book?
- At this rate, how many books can you buy for $21?
-
Neon bracelets cost $1 for 4.
- What is the cost per bracelet?
- At this rate, how much will 11 neon bracelets cost?
Pause here so your teacher can review your work.

- Your teacher will assign you one of the problems. Create a visual display that shows your solution to the problem. Be prepared to share your solution with the class.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The first and third questions involve using decimals to represent cents. If the decimal point is forgotten, remind students that the cost of the bracelet is less than one dollar, and the cost of the chips is in between one and two dollars.
Watch for students working in cents instead of dollars for the bracelets. They may come up with an answer of 275 cents. For these students, writing 25 cents as \$0.25 should help, or consider reminding them of the avocados from a previous activity, which had a unit price of \$0.50.
Activity Synthesis
Invite each group to present its assigned problem. After each group presents, highlight the group’s strategy, accurate uses of the terms “at this rate” and “per,” and the ways in which a double number line might have been used when working with unit price.
Lesson Synthesis
Lesson Synthesis
The main ideas to develop in this lesson are techniques for finding a unit price, and the things that can be done once a unit price is known.
Discuss with students the methods they use to find a unit price. The likely answers are:
- Division: if 2 bags of rice cost \$3, then 1 bag costs \(3 \div 2 = 1.50\).
- Double number line: adding tick marks to a double number line signifying 1 bag can determine the cost per bag. Briefly discuss with students the meaning of the word per (for each).
Discuss with students the things they can do once they know a unit price. Specifically, they can directly compute any cost when the number of items is known by multiplying the unit price by the number of items. You may want to point out to students that by multiplying, they are finding part of an equivalent ratio. For example, the ratio “\$30 for 20 bags“ is equivalent to the ratio “\$3 for 2 bags.”
8.4: Cool-down - Unit Price of Rice (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The unit price is the price of 1 thing—for example, the price of 1 ticket, 1 slice of pizza, or 1 kilogram of peaches.
If 4 movie tickets cost \$28, then the unit price would be the cost per ticket. We can create a double number line to find the unit price.
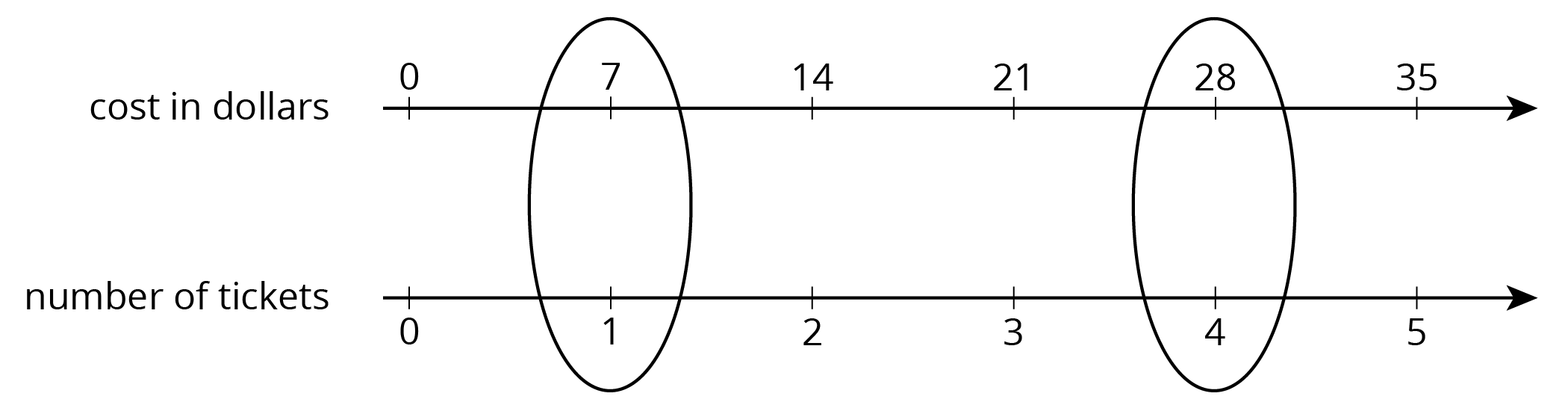
This double number line shows that the cost for 1 ticket is \$7. We can also find the unit price by dividing, \(28 \div 4 = 7\), or by multiplying, \(28 \boldcdot \frac14 = 7\).