Lesson 2
Representing Ratios with Diagrams
Problem 1
Here is a diagram that describes the cups of green and white paint in a mixture.

Select all the statements that correctly describe this diagram
The ratio of cups of white paint to cups of green paint is 2 to 4.
For every cup of green paint, there are two cups of white paint.
The ratio of cups of green paint to cups of white paint is \(4:2\).
For every cup of white paint, there are two cups of green paint.
The ratio of cups of green paint to cups of white paint is \(2:4\).
Solution
For access, consult one of our IM Certified Partners.
Problem 2
To make a snack mix, combine 2 cups of raisins with 4 cups of pretzels and 6 cups of almonds.
-
Create a diagram to represent the quantities of each ingredient in this recipe.
-
Use your diagram to complete each sentence.
- The ratio of __________________ to __________________ to __________________ is ________ : ________ : ________.
- There are ________ cups of pretzels for every cup of raisins.
- There are ________ cups of almonds for every cup of raisins.
Solution
For access, consult one of our IM Certified Partners.
Problem 3
- A square is 3 inches by 3 inches. What is its area?
- A square has a side length of 5 feet. What is its area?
- The area of a square is 36 square centimeters. What is the length of each side of the square?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 1, Lesson 17.)Problem 4
Find the area of this quadrilateral. Explain or show your strategy.
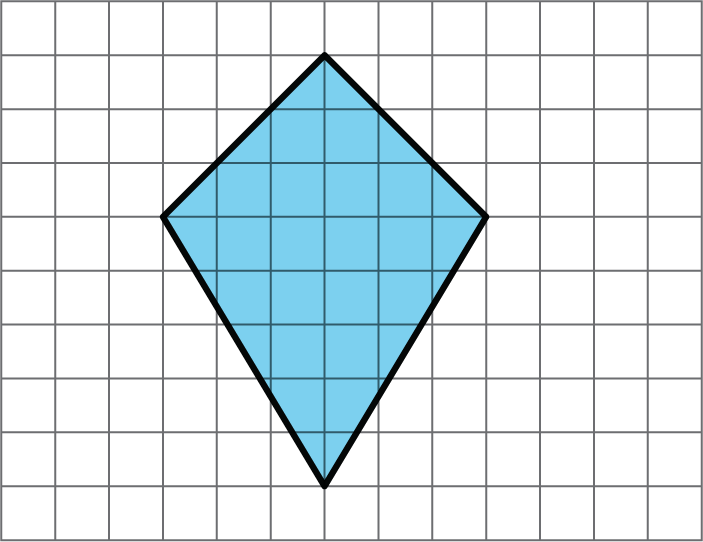
Solution
For access, consult one of our IM Certified Partners.
(From Unit 1, Lesson 11.)Problem 5
Complete each equation with a number that makes it true.
- \(\frac18 \boldcdot 8 = \text{_______}\)
- \(\frac38 \boldcdot 8 = \text{_______}\)
- \(\frac18 \boldcdot 7 = \text{_______}\)
- \(\frac38 \boldcdot 7 = \text{_______}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 2, Lesson 1.)