Lesson 2
Representing Ratios with Diagrams
Let’s use diagrams to represent ratios.
2.1: Number Talk: Dividing by 4 and Multiplying by $\frac14$
Find the value of each expression mentally.
\(24\div 4\)
\(\frac14\boldcdot 24\)
\(24\boldcdot \frac14\)
\(5\div 4\)
2.2: A Collection of Snap Cubes
Here is a collection of snap cubes.

- Choose two of the colors in the image, and draw a diagram showing the number of snap cubes for these two colors.
- Trade papers with a partner. On their paper, write a sentence to describe a ratio shown in their diagram. Your partner will do the same for your diagram.
- Return your partner’s paper. Read the sentence written on your paper. If you disagree, explain your thinking.
2.3: Blue Paint and Art Paste
Elena mixed 2 cups of white paint with 6 tablespoons of blue paint.
Here is a diagram that represents this situation.

-
Discuss each statement, and circle all those that correctly describe this situation. Make sure that both you and your partner agree with each circled answer.
- The ratio of cups of white paint to tablespoons of blue paint is \(2 : 6\).
- For every cup of white paint, there are 2 tablespoons of blue paint.
- There is 1 cup of white paint for every 3 tablespoons of blue paint.
- There are 3 tablespoons of blue paint for every cup of white paint.
- For each tablespoon of blue paint, there are 3 cups of white paint.
- For every 6 tablespoons of blue paint, there are 2 cups of white paint.
- The ratio of tablespoons of blue paint to cups of white paint is 6 to 2.
-
Jada mixed 8 cups of flour with 2 pints of water to make paste for an art project.
-
Draw a diagram that represents the situation.
- Write at least two sentences describing the ratio of flour and water.
-
2.4: Card Sort: Spaghetti Sauce
Your teacher will give you cards describing different recipes for spaghetti sauce. In the diagrams:
- a circle represents a cup of tomato sauce
- a square represents a tablespoon of oil
- a triangle represents a teaspoon of oregano

-
Take turns with your partner to match a sentence with a diagram.
- For each match that you find, explain to your partner how you know it’s a match.
- For each match that your partner finds, listen carefully to their explanation. If you disagree, discuss your thinking and work to reach an agreement.
- After you and your partner have agreed on all of the matches, check your answers with the answer key. If there are any errors, discuss why and revise your matches.
-
There were two diagrams that each matched with two different sentences. Which were they?
- Diagram _______ matched with both sentences ______ and ______.
- Diagram _______ matched with both sentences ______ and ______.
- Select one of the other diagrams and invent another sentence that could describe the ratio shown in the diagram.
Create a diagram that represents any of the ratios in a recipe of your choice. Is it possible to include more than 2 ingredients in your diagram?
Summary
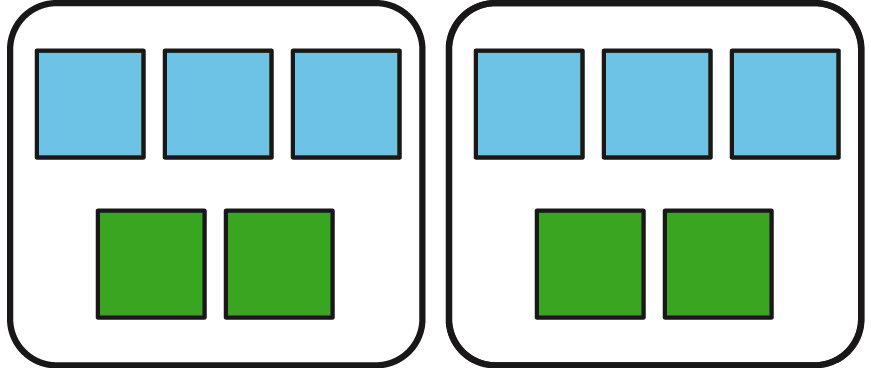
Ratios can be represented using diagrams. The diagrams do not need to include realistic details. For example, a recipe for lemonade says, “Mix 2 scoops of lemonade powder with 6 cups of water.”
Instead of this:
We can draw something like this:

This diagram shows that the ratio of cups of water to scoops of lemonade powder is 6 to 2. We can also see that for every scoop of lemonade powder, there are 3 cups of water.
Glossary Entries
- ratio
A ratio is an association between two or more quantities.
For example, the ratio \(3:2\) could describe a recipe that uses 3 cups of flour for every 2 eggs, or a boat that moves 3 meters every 2 seconds. One way to represent the ratio \(3:2\) is with a diagram that has 3 blue squares for every 2 green squares.