Lesson 13

Interpreting Points on a Coordinate Plane

Let’s examine what points on the coordinate plane can tell us.

Problem 1

The elevation of a submarine is shown in the table. Draw and label coordinate axes with an appropriate scale and plot the points.

time after noon (hours) elevation (meters)
0 -567
1 -892
2 -1,606
3 -1,289
4 -990
5 -702
6 -365

 

Problem 2

The inequalities \(h > 42\) and \(h< 60\) represent the height requirements for an amusement park ride, where \(h\) represents a person's height in inches.

Write a sentence or draw a sign that describes these rules as clearly as possible.

(From Unit 7, Lesson 8.)

Problem 3

The \(x\)-axis represents the number of hours before or after noon, and the \(y\)-axis represents the temperature in degrees Celsius.

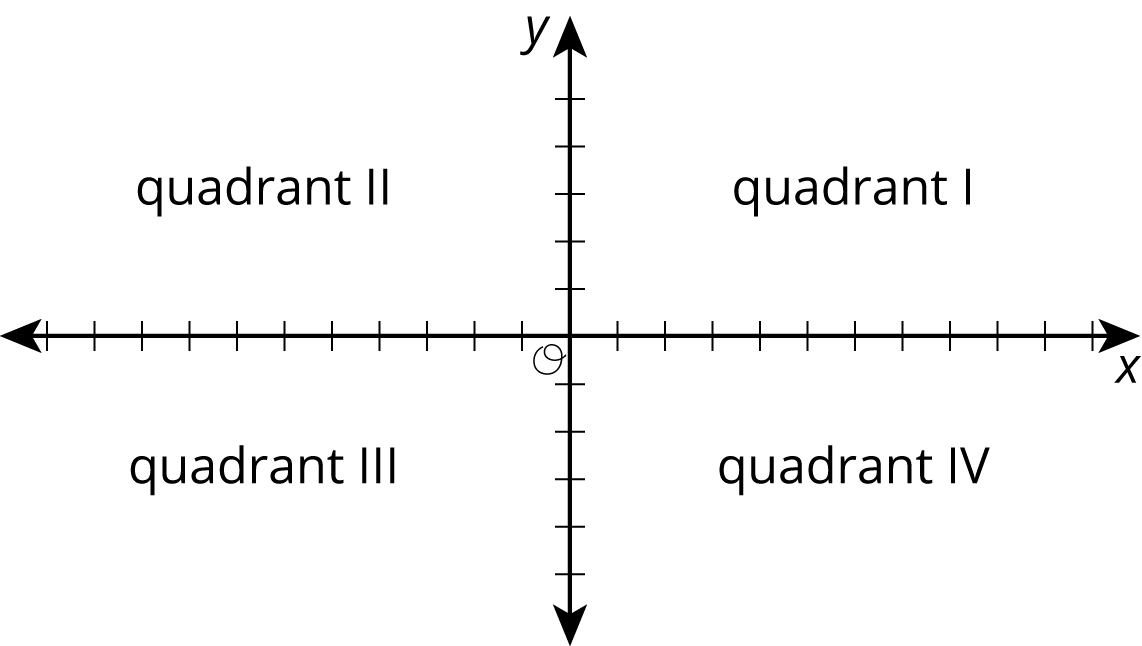
A coordinate plane, origin O. The area top & right of the origin is Quadrant 1, and counter-clockwise labeled quadrant 2, 3, 4.

  1. At 9 a.m., it was below freezing. In what quadrant would this point be plotted?

  2. At 11 a.m., it was \(10^\circ \text{C}\). In what quadrant would this point be plotted?

  3. Choose another time and temperature. Then tell the quadrant where the point should be plotted.

  4. What does the point \((0, 0)\) represent in this context?

Problem 4

Solve each equation.

\(3a = 12\)

\(b + 3.3 = 8.9\)

\(1 = \frac{1}{4} c\)

\(5\frac{1}{2} = d+ \frac{1}{4} \)

\(2e = 6.4\)

(From Unit 6, Lesson 4.)