Lesson 9
Solutions of Inequalities
Let’s think about the solutions to inequalities.
9.1: Unknowns on a Number Line
The number line shows several points, each labeled with a letter.

-
Fill in each blank with a letter so that the inequality statements are true.
- _______ > _______
- _______ < _______
- Jada says that she found three different ways to complete the first question correctly. Do you think this is possible? Explain your reasoning.
- List a possible value for each letter on the number line based on its location.
9.2: Amusement Park Rides
Priya finds these height requirements for some of the rides at an amusement park.
| To ride the . . . | you must be . . . |
|---|---|
| High Bounce | between 55 and 72 inches tall |
| Climb-A-Thon | under 60 inches tall |
| Twirl-O-Coaster | 58 inches minimum |
-
Write an inequality for each of the the three height requirements. Use \(h\) for the unknown height. Then, represent each height requirement on a number line.
-
High Bounce

-
Climb-A-Thon

-
Twirl-O-Coaster

Pause here for additional instructions from your teacher.
-
- Han’s cousin is 55 inches tall. Han doesn’t think she is tall enough to ride the High Bounce, but Kiran believes that she is tall enough. Do you agree with Han or Kiran? Be prepared to explain your reasoning.
-
Priya can ride the Climb-A-Thon, but she cannot ride the High Bounce or the Twirl-O-Coaster. Which, if any, of the following could be Priya’s height? Be prepared to explain your reasoning.
- 59 inches
- 53 inches
- 56 inches
- Jada is 56 inches tall. Which rides can she go on?
- Kiran is 60 inches tall. Which rides can he go on?
-
The inequalities \(h < 75\) and \(h > 64\) represent the height restrictions, in inches, of another ride. Write three values that are solutions to both of these inequalities.
-
Represent the height restrictions for all three rides on a single number line, using a different color for each ride.

- Which part of the number line is shaded with all 3 colors?
- Name one possible height a person could be in order to go on all three rides.
9.3: What Number Am I?
Your teacher will give your group two sets of cards—one set shows inequalities and the other shows numbers. Place the inequality cards face up where everyone can see them. Shuffle the number cards and stack them face down.
To play:
-
One person in your group is the detective. The other people will give clues.
-
Pick one number card from the stack and show it to everyone except the detective.
-
The people giving clues each choose an inequality that will help the detective identify the unknown number.
-
The detective studies the inequalities and makes three guesses.
-
If the detective does not guess the right number, each person chooses another inequality to help.
-
When the detective does guess the right number, a new person becomes the detective.
-
-
Repeat the game until everyone has had a turn being the detective.
Summary
Let’s say a movie ticket costs less than \$10. If \(c\) represents the cost of a movie ticket, we can use \(c < 10\) to express what we know about the cost of a ticket.
Any value of \(c\) that makes the inequality true is called a solution to the inequality.
For example, 5 is a solution to the inequality \(c < 10\) because \(5<10\) (or “5 is less than 10”) is a true statement, but 12 is not a solution because \(12<10\) (“12 is less than 10”) is not a true statement.
If a situation involves more than one boundary or limit, we will need more than one inequality to express it.
For example, if we knew that it rained for more than 10 minutes but less than 30 minutes, we can describe the number of minutes that it rained (\(r\)) with the following inequalities and number lines. \(\displaystyle r > 10\)
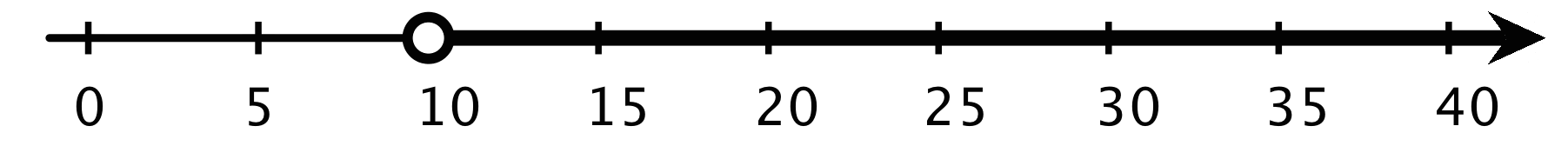
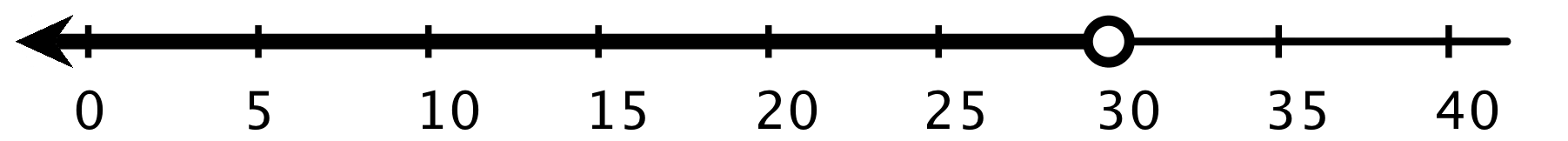
Any number of minutes greater than 10 is a solution to \(r>10\), and any number less than 30 is a solution to \(r<30\). But to meet the condition of “more than 10 but less than 30,” the solutions are limited to the numbers between 10 and 30 minutes, not including 10 and 30.
We can show the solutions visually by graphing the two inequalities on one number line.
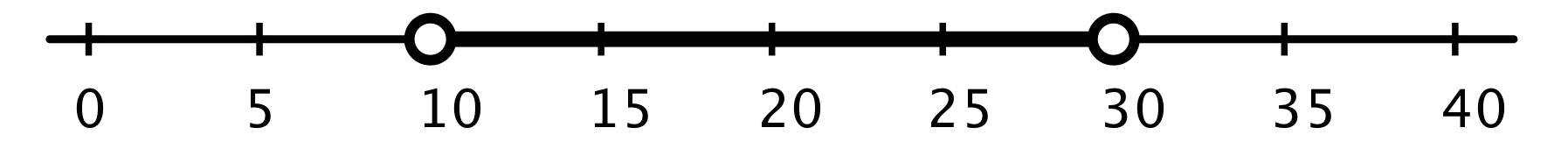
Glossary Entries
- solution to an inequality
A solution to an inequality is a number that can be used in place of the variable to make the inequality true.
For example, 5 is a solution to the inequality \(c<10\), because it is true that \(5<10\). Some other solutions to this inequality are 9.9, 0, and -4.