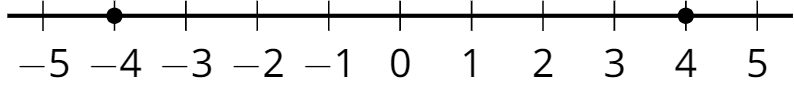Lesson 5
Using Negative Numbers to Make Sense of Contexts
Let’s make sense of negative amounts of money.
5.1: Notice and Wonder: It Comes and Goes
| activity | amount |
|---|---|
| do my chores | 30.00 |
| babysit my cousin | 45.00 |
| buy my lunch | -10.80 |
| get my allowance | 15.00 |
| buy a shirt | -18.69 |
| pet my dog | 0.00 |
What do you notice? What do you wonder?
5.2: The Concession Stand
The manager of the concession stand keeps records of all of the supplies she buys and all of the items she sells. The table shows some of her records for Tuesday.
| item | quantity | value in dollars |
|---|---|---|
| doughnuts | -58 | 37.70 |
| straws | 3,000 | -10.35 |
| hot dogs | -39 | 48.75 |
| pizza | 13 | -116.87 |
| apples | -40 | 14.00 |
| french fries | -88 | 132.00 |
- Which items did she sell? Explain your reasoning.
- How can we interpret -58 in this situation?
- How can we interpret -10.35 in this situation?
- On which item did she spend the most amount of money? Explain your reasoning.
5.3: Drinks for Sale
A vending machine in an office building sells bottled beverages. The machine keeps track of all changes in the number of bottles from sales and from machine refills and maintenance. This record shows the changes for every 5-minute period over one hour.
- What might a positive number mean in this context? What about a negative number?
- What would a “0” in the second column mean in this context?
- Which numbers—positive or negative—result in fewer bottles in the machine?
- At what time was there the greatest change to the number of bottles in the machine? How did that change affect the number of remaining bottles in the machine?
- At which time period, 8:05–8:09 or 8:25–8:29, was there a greater change to the number of bottles in the machine? Explain your reasoning.
- The machine must be emptied to be serviced. If there are 40 bottles in the machine when it is to be serviced, what number will go in the second column in the table?
| time | number of bottles |
|---|---|
| 8:00–8:04 | -1 |
| 8:05–8:09 | +12 |
| 8:10–8:14 | -4 |
| 8:15–8:19 | -1 |
| 8:20–8:24 | -5 |
| 8:25–8:29 | -12 |
| 8:30–8:34 | -2 |
| 8:35–8:39 | 0 |
| 8:40–8:44 | 0 |
| 8:45–8:49 | -6 |
| 8:50–8:54 | +24 |
| 8:55–8:59 | 0 |
| service |
Priya, Mai, and Lin went to a cafe on a weekend. Their shared bill came to \$25. Each student gave the server a \$10 bill. The server took this \$30 and brought back five \$1 bills in change. Each student took \$1 back, leaving the rest, \$2, as a tip for the server.
As she walked away from the cafe, Lin thought, “Wait—this doesn’t make sense. Since I put in \$10 and got \$1 back, I wound up paying \$9. So did Mai and Priya. Together, we paid \$27. Then we left a \$2 tip. That makes \$29 total. And yet we originally gave the waiter \$30. Where did the extra dollar go?”
Think about the situation and about Lin’s question. Do you agree that the numbers didn’t add up properly? Explain your reasoning.
Summary
Sometimes we represent changes in a quantity with positive and negative numbers. If the quantity increases, the change is positive. If it decreases, the change is negative.
- Suppose 5 gallons of water is put in a washing machine. We can represent the change in the number of gallons as +5. If 3 gallons is emptied from the machine, we can represent the change as -3.
It is especially common to represent money we receive with positive numbers and money we spend with negative numbers.
- Suppose Clare gets \$30.00 for her birthday and spends \$18.00 buying lunch for herself and a friend. To her, the value of the gift can be represented as +30.00 and the value of the lunch as -18.00.
Whether a number is considered positive or negative depends on a person’s perspective. If Clare’s grandmother gives her \$20 for her birthday, Clare might see this as +20, because to her, the amount of money she has increased. But her grandmother might see it as -20, because to her, the amount of money she has decreased.
In general, when using positive and negative numbers to represent changes, we have to be very clear about what it means when the change is positive and what it means when the change is negative.
Video Summary
Glossary Entries
- negative number
A negative number is a number that is less than zero. On a horizontal number line, negative numbers are usually shown to the left of 0.
- opposite
Two numbers are opposites if they are the same distance from 0 and on different sides of the number line.
For example, 4 is the opposite of -4, and -4 is the opposite of 4. They are both the same distance from 0. One is negative, and the other is positive.
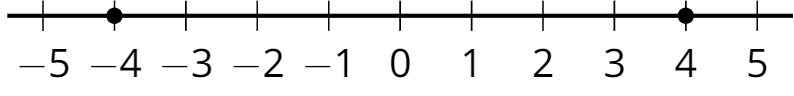
- positive number
A positive number is a number that is greater than zero. On a horizontal number line, positive numbers are usually shown to the right of 0.
- rational number
A rational number is a fraction or the opposite of a fraction.
For example, 8 and -8 are rational numbers because they can be written as \(\frac81\) and \(\text-\frac81\).
Also, 0.75 and -0.75 are rational numbers because they can be written as \(\frac{75}{100}\) and \(\text-\frac{75}{100}\).
- sign
The sign of any number other than 0 is either positive or negative.
For example, the sign of 6 is positive. The sign of -6 is negative. Zero does not have a sign, because it is not positive or negative.