Lesson 18
Using Common Multiples and Common Factors
Let’s use common factors and common multiple to solve problems.
18.1: Keeping a Steady Beat
Your teacher will give you instructions for playing a rhythm game. As you play the game, think about these questions:
- When will the two sounds happen at the same time?
- How does this game relate to common factors or common multiples?
18.2: Factors and Multiples
Work with your partner to solve the following problems.
-
Party. Elena is buying cups and plates for her party. Cups are sold in packs of 8 and plates are sold in packs of 6. She wants to have the same number of plates and cups.
- Find a number of plates and cups that meets her requirement.
- How many packs of each supply will she need to buy to get that number?
- Name two other quantities of plates and cups she could get to meet her requirement.
-
Tiles. A restaurant owner is replacing the restaurant’s bathroom floor with square tiles. The tiles will be laid side-by-side to cover the entire bathroom with no gaps, and none of the tiles can be cut. The floor is a rectangle that measures 24 feet by 18 feet.
- What is the largest possible tile size she could use? Write the side length in feet. Explain how you know it’s the largest possible tile.
- How many of these largest size tiles are needed?
- Name more tile sizes that are whole number of feet that she could use to cover the bathroom floor. Write the side lengths (in feet) of the square tiles.
-
Stickers. To celebrate the first day of spring, Lin is putting stickers on some of the 100 lockers along one side of her middle school’s hallway. She puts a skateboard sticker on every 4th locker (starting with locker 4), and a kite sticker on every 5th locker (starting with locker 5).
- Name three lockers that will get both stickers.
- After Lin makes her way down the hall, will the 30th locker have no stickers, 1 sticker, or 2 stickers? Explain how you know.
-
Kits. The school nurse is assembling first-aid kits for the teachers. She has 75 bandages and 90 throat lozenges. All the kits must have the same number of each supply, and all supplies must be used.
- What is the largest number of kits the nurse can make?
- How many bandages and lozenges will be in each kit?
-
What kind of mathematical work was involved in each of the previous problems? Put a checkmark to show what the questions were about.
problem finding multiples finding least
common multiplefinding factors finding greatest
common factorParty Tiles Stickers Kits
You probably know how to draw a five-pointed star without lifting your pencil. One way to do this is to start with five dots arranged in a circle, then connect every second dot.

If you try the same thing with six dots arranged in a circle, you will have to lift your pencil. Once you make the first triangle, you’ll have to find an empty dot and start the process over. Your six-pointed star has two pieces that are each drawn without lifting the pencil.
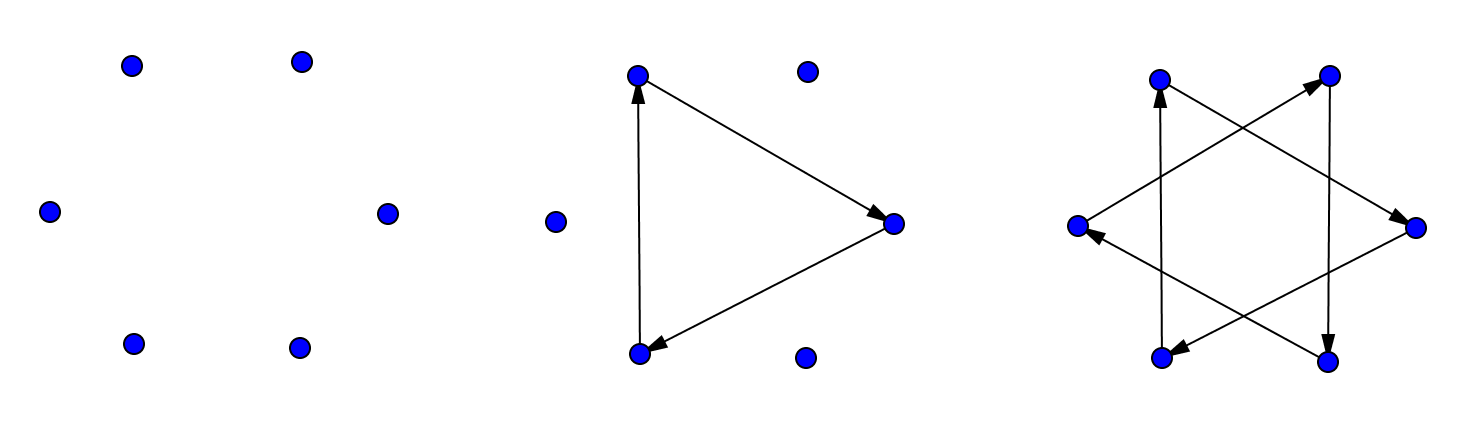
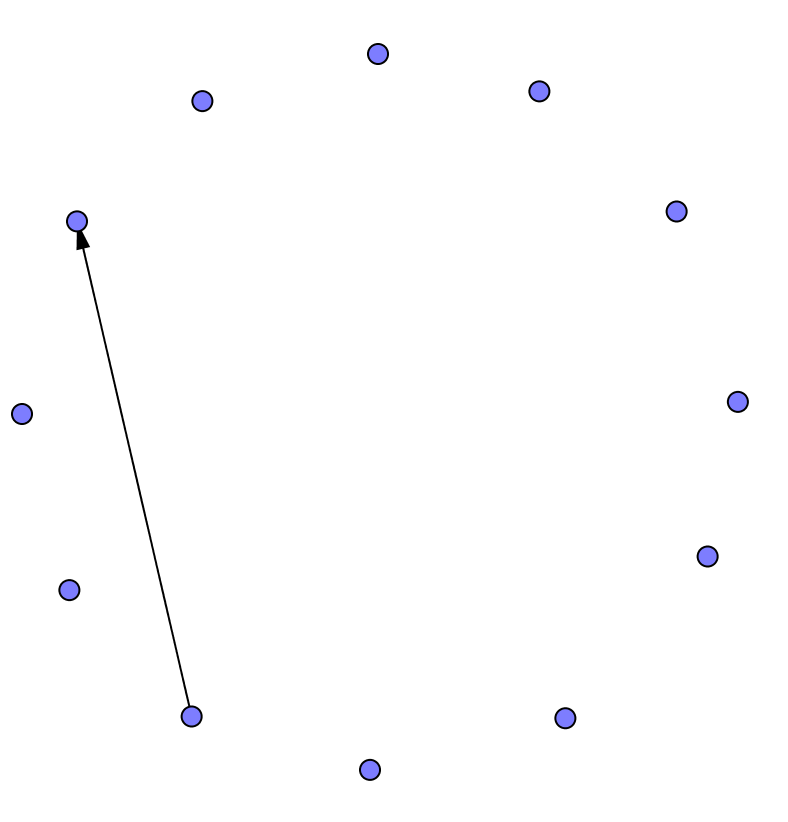
With twelve dots arranged in a circle, we can make some twelve-pointed stars.
-
Start with one dot and connect every second dot, as if you were drawing a five-pointed star. Can you draw the twelve-pointed star without lifting your pencil? If not, how many pieces does the twelve-pointed star have?

-
This time, connect every third dot. Can you draw this twelve-pointed star without lifting your pencil? If not, how many pieces do you get?
-
What do you think will happen if you connect every fourth dot? Try it. How many pieces do you get?

-
Do you think there is any way to draw a twelve-pointed star without lifting your pencil? Try it out.

- Now investigate eight-pointed stars, nine-pointed stars, and ten-pointed stars. What patterns do you notice?
18.3: More Factors and Multiples
Here are five more problems. Read and discuss each one with your group. Without solving, predict whether each problem involves finding common multiples or finding common factors. Circle one or more options to show your prediction.
-
Soccer. Diego and Andre are both in a summer soccer league. During the month of August, Diego has a game every 3rd day, starting August 3rd, and Andre has a game every 4th day, starting August 4th.
- common multiples
- least common multiple
- common factors
- greatest common factor
- What is the first date that both boys will have a game?
- How many of their games fall on the same date?
-
Performances. During a performing arts festival, students from elementary and middle schools will be grouped together for various performances. There are 32 elementary students and 40 middle-school students. The arts director wants identical groups for the performances, with students from both schools in each group. Each student can be a part of only one group.
- common multiples
- least common multiple
- common factors
- greatest common factor
- Name all possible groupings.
- What is the largest number of groups that can be formed? How many elementary school students and how many middle school students will be in each group?
-
Lights. There is a string of holiday lights with red, gold, and blue lights. The red lights are set to blink every 12 seconds, the gold lights are set to blink every 8 seconds, and the blue lights are set to blink every 6 seconds. The lights are on an automatic timer that starts each day at 7:00 p.m. and stops at midnight.
- common multiples
- least common multiple
- common factors
- greatest common factor
- After how much time with all 3 lights blink at the exact same time?
- How many times total will this happen in one day?
-
Banners. Noah has two pieces of cloth. He is making square banners for students to hold during the opening day game. One piece of cloth is 72 inches wide. The other is 90 inches wide. He wants to use all the cloth, and each square banner must be of equal width and as wide as possible.
- common multiples
- least common multiple
- common factors
- greatest common factor
- How wide should he cut the banners?
- How many banners can he cut?
-
Dancers. At Elena’s dance recital her performance begins with a line of 48 dancers that perform in the dark with a black light that illuminates white clothing. All 48 dancers enter the stage in a straight line. Every 3rd dancer wears a white headband, every 5th dancer wears a white belt, and every 9th dancer wears a set of white gloves.
- common multiples
- least common multiple
- common factors
- greatest common factor
- If Elena is the 30th dancer, what accessories will she wear?
- Will any of the dancers wear all 3 accessories? If so, which one(s)?
- How many of each accessory will the dance teacher need to order?
-
Your teacher will assign your group a problem. Work with your group to solve the problem. Show your reasoning. Pause here so your teacher can review your work.
-
Work with your group to create a visual display that includes a diagram, an equation, and a math vocabulary word that would help to explain your mathematical thinking while solving the problem.
-
Prepare a short presentation in which all group members are involved. Your presentation should include: the problem (read aloud), your group's prediction of what mathematical concept the problem involved, and an explanation of each step of the solving process.
18.4: Factors and Multiples Bingo
Your teacher will explain the directions for a bingo game. Here are some things to keep in mind:
-
Share one bingo board and some bingo chips with a partner.
-
To play the game, your teacher will read statements aloud. You may help one another decide what numbers fit each statement, but speak only in a whisper. If the teacher hears anything above a whisper, you are out.
-
The first person to call bingo needs to call out each number and identify the statement that it corresponds to. If there is an error in identifying statements, that player is out and the round continues.
Good luck, and have fun!
Summary
If a problem requires dividing two whole numbers by the same whole number, solving it involves looking for a common factor. If it requires finding the largest number that can divide into the two whole numbers, we are looking for the greatest common factor.
Suppose we have 12 bagels and 18 muffins and want to make bags so each bag has the same combination of bagels and muffins. The common factors of 12 and 18 tell us possible number of bags that can be made.
The common factors of 12 and 18 are 1, 2, 3, and 6. For these numbers of bags, here are the number of bagels and muffins per bag.
- 1 bag: 12 bagels and 18 muffins
- 2 bags: 6 bagels and 9 muffins
- 3 bags: 4 bagels and 6 muffins
- 6 bags: 2 bagels and 3 muffins
We can see that the largest number of bags that can be made, 6, is the greatest common factor.
If a problem requires finding a number that is a multiple of two given numbers, solving it involves looking for a common multiple. If it requires finding the first instance the two numbers share a multiple, we are looking for the least common multiple.
Suppose forks are sold in boxes of 9 and spoons are sold in boxes of 15, and we want to buy an equal number of each. The multiples of 9 tell us how many forks we could buy, and the multiples of 15 tell us how many spoons we could buy, as shown here.
- Forks: 9, 18, 27, 36, 45, 54, 63, 72, 90. . .
- Spoons: 15, 30, 45, 60, 75, 90. . .
If we want as many forks as spoons, our options are 45, 90, 135, and so on, but the smallest number of utensils we could buy is 45, the least common multiple. This means buying 5 boxes of forks (\(5\boldcdot 9=45\)) and 3 boxes of spoons (\(3 \boldcdot 15=45\)).
Video Summary
Glossary Entries
- common factor
A common factor of two numbers is a number that divides evenly into both numbers. For example, 5 is a common factor of 15 and 20, because \(15 \div 5 = 3\) and \(20 \div 5 = 4\). Both of the quotients, 3 and 4, are whole numbers.
- The factors of 15 are 1, 3, 5, and 15.
- The factors of 20 are 1, 2, 4, 5, 10, and 20.
- common multiple
A common multiple of two numbers is a product you can get by multiplying each of the two numbers by some whole number. For example, 30 is a common multiple of 3 and 5, because \(3 \cdot 10 = 30\) and \(5 \cdot 6 = 30\). Both of the factors, 10 and 6, are whole numbers.
- The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 . . .
- The multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40 . . .
The common multiples of 3 and 5 are 15, 30, 45, 60 . . .
- greatest common factor
The greatest common factor of two numbers is the largest number that divides evenly into both numbers. Sometimes we call this the GCF. For example, 15 is the greatest common factor of 45 and 60.
- The factors of 45 are 1, 3, 5, 9, 15, and 45.
- The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
- least common multiple
The least common multiple of two numbers is the smallest product you can get by multiplying each of the two numbers by some whole number. Sometimes we call this the LCM. For example, 30 is the least common multiple of 6 and 10.
- The multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 . . .
- The multiples of 10 are 10, 20, 30, 40, 50, 60, 70, 80 . . .