Lesson 7
Comparing Numbers and Distance from Zero
Let’s use absolute value and negative numbers to think about elevation.
7.1: Opposites
-
\(a\) is a rational number. Choose a value for \(a\) and plot it on the number line.
-
- Based on where you plotted \(a\), plot \(\text- a\) on the same number line.
- What is the value of \(\text- a\) that you plotted?
- Noah said, “If \(a\) is a rational number, \(\text- a\) will always be a negative number.” Do you agree with Noah? Explain your reasoning.
7.2: Submarine
A submarine is at an elevation of -100 feet (100 feet below sea level). Let’s compare the elevations of these four people to that of the submarine:
- Clare’s elevation is greater than the elevation of the submarine. Clare is farther from sea level than the submarine.
- Andre’s elevation is less than the elevation of the submarine. Andre is farther away from sea level than the submarine.
- Han’s elevation is greater than the elevation of the submarine. Han is closer to sea level than is the submarine.
- Lin’s elevation is the same distance away from sea level as the submarine’s.
-
Complete the table as follows.
- Write a possible elevation for each person.
- Use \(<\), \(>\), or \(=\) to compare the elevation of that person to that of the submarine.
- Use absolute value to tell how far away the person is from sea level (elevation 0).
possible
elevationcompare to
submarinedistance from
sea levelClare 150 feet \(150 > \text-100\) \(|150|\) or 150 feet Andre Han Lin - Priya says her elevation is less than the submarine’s and she is closer to sea level. Is this possible? Explain your reasoning.
7.3: Info Gap: Points on the Number Line
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
7.4: Inequality Mix and Match
Here are some numbers and inequality symbols. Work with your partner to write true comparison statements.
-0.7
\(\text{-}\frac {3}{5}\)
1
4
\(|\text-8|\)
\(<\)
\(\text{-}\frac {6}{3}\)
-2.5
2.5
8
\(|0.7|\)
\(=\)
-4
0
\(\frac72\)
\(|3|\)
\(|\text{-}\frac {5}{2}|\)
\(>\)
One partner should select two numbers and one comparison symbol and use them to write a true statement using symbols. The other partner should write a sentence in words with the same meaning, using the following phrases:
- is equal to
- is the absolute value of
- is greater than
- is less than
For example, one partner could write \(4 < 8\) and the other would write, “4 is less than 8.” Switch roles until each partner has three true mathematical statements and three sentences written down.
For each question, choose a value for each variable to make the whole statement true. (When the word and is used in math, both parts have to be true for the whole statement to be true.) Can you do it if one variable is negative and one is positive? Can you do it if both values are negative?
- \(x < y\) and \(|x| < y\).
- \(a < b\) and \(|a| < |b|\).
- \(c < d\) and \(|c| > d\).
- \(t < u\) and \(|t| > |u|\).
Summary
We can use elevation to help us compare two rational numbers or two absolute values.
- Suppose an anchor has an elevation of -10 meters and a house has an elevation of 12 meters. To describe the anchor having a lower elevation than the house, we can write \(\text-10<12\) and say “-10 is less than 12.”
- The anchor is closer to sea level than the house is to sea level (or elevation of 0). To describe this, we can write \(|\text-10|<|12|\) and say “the distance between -10 and 0 is less than the distance between 12 and 0.”
We can use similar descriptions to compare rational numbers and their absolute values outside of the context of elevation.
- To compare the distance of -47.5 and 5.2 from 0, we can say: \(|\text-47.5|\) is 47.5 units away from 0, and \(|5.2|\) is 5.2 units away from 0, so \(|\text-47.5|>|5.2|\).
- \(|\text-18|>4\) means that the absolute value of -18 is greater than 4. This is true because 18 is greater than 4.
Video Summary
Glossary Entries
- absolute value
The absolute value of a number is its distance from 0 on the number line.
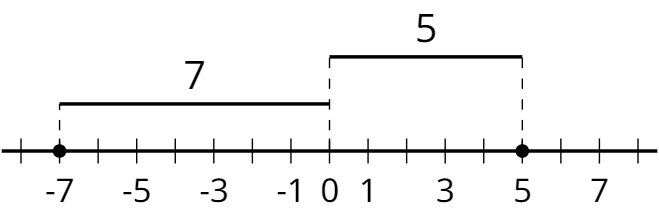
The absolute value of -7 is 7, because it is 7 units away from 0. The absolute value of 5 is 5, because it is 5 units away from 0.
- negative number
A negative number is a number that is less than zero. On a horizontal number line, negative numbers are usually shown to the left of 0.
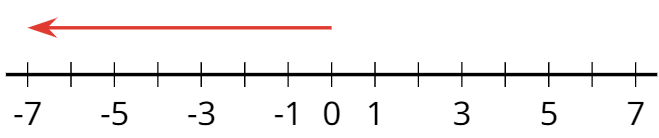
- opposite
Two numbers are opposites if they are the same distance from 0 and on different sides of the number line.
For example, 4 is the opposite of -4, and -4 is the opposite of 4. They are both the same distance from 0. One is negative, and the other is positive.
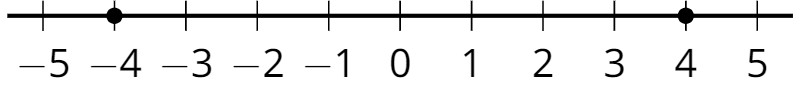
- positive number
A positive number is a number that is greater than zero. On a horizontal number line, positive numbers are usually shown to the right of 0.
- rational number
A rational number is a fraction or the opposite of a fraction.
For example, 8 and -8 are rational numbers because they can be written as \(\frac81\) and \(\text-\frac81\).
Also, 0.75 and -0.75 are rational numbers because they can be written as \(\frac{75}{100}\) and \(\text-\frac{75}{100}\).
- sign
The sign of any number other than 0 is either positive or negative.
For example, the sign of 6 is positive. The sign of -6 is negative. Zero does not have a sign, because it is not positive or negative.