Lesson 3
Comparing Proportional Relationships
Problem 1
A contractor must haul a large amount of dirt to a work site. She collected information from two hauling companies.
EZ Excavation gives its prices in a table.
| dirt (cubic yards) |
cost (dollars) |
|---|---|
| 8 | 196 |
| 20 | 490 |
| 26 | 637 |
Happy Hauling Service gives its prices in a graph.
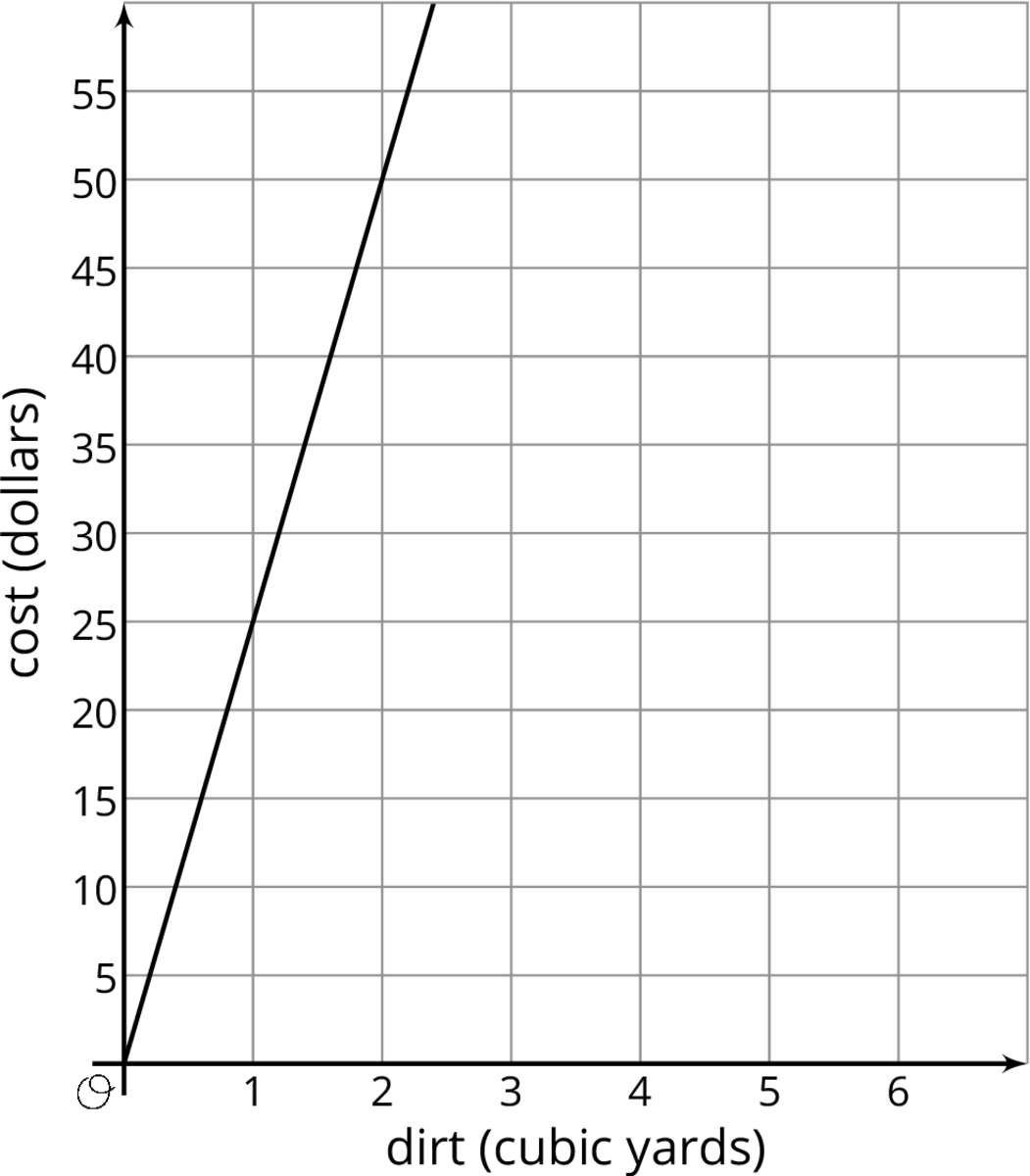
- How much would each hauling company charge to haul 40 cubic yards of dirt? Explain or show your reasoning.
- Calculate the rate of change for each relationship. What do they mean for each company?
- If the contractor has 40 cubic yards of dirt to haul and a budget of $1000, which hauling company should she hire? Explain or show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Andre and Priya are tracking the number of steps they walk. Andre records that he can walk 6000 steps in 50 minutes. Priya writes the equation \(y=118x\), where \(y\) is the number of steps and \(x\) is the number of minutes she walks, to describe her step rate. This week, Andre and Priya each walk for a total of 5 hours. Who walks more steps? How many more?
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Find the coordinates of point \(D\) in each diagram:
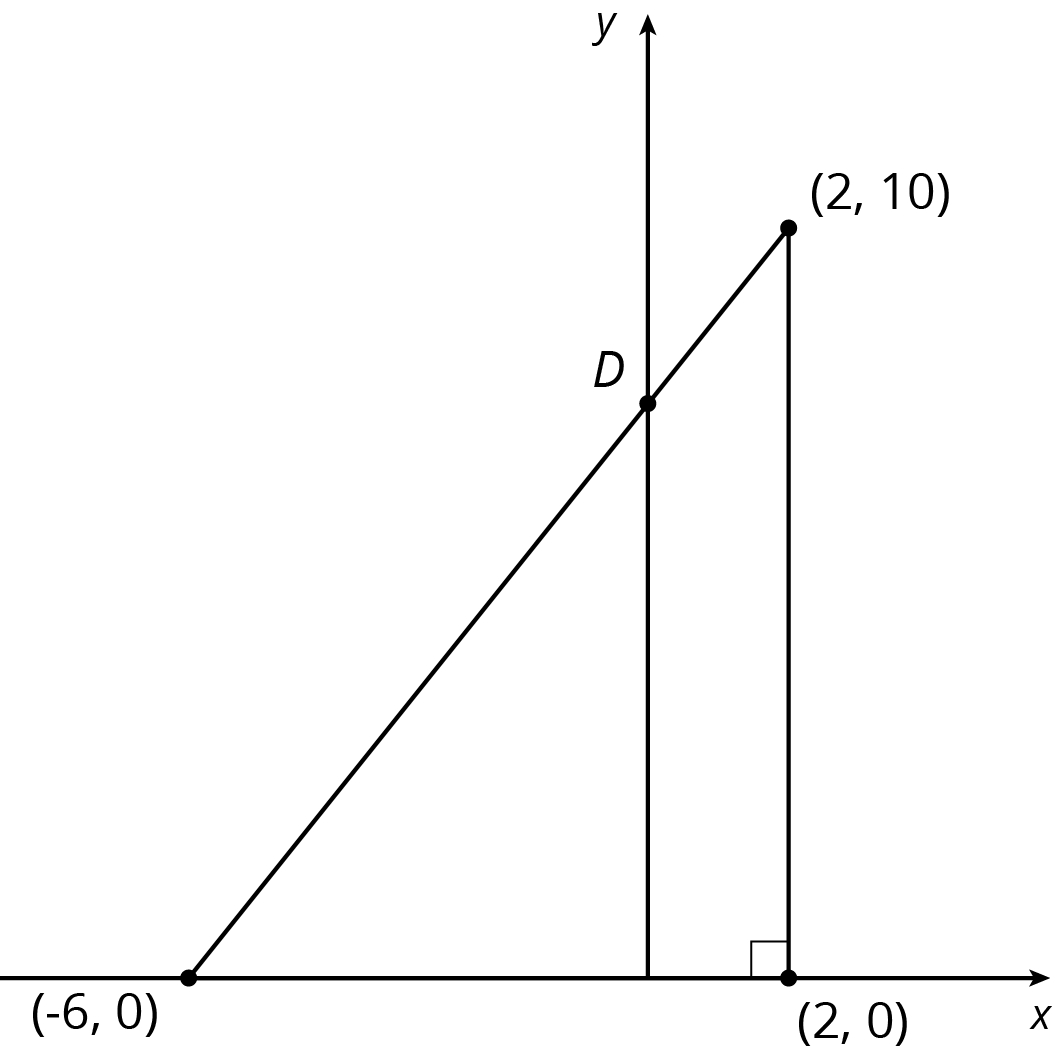
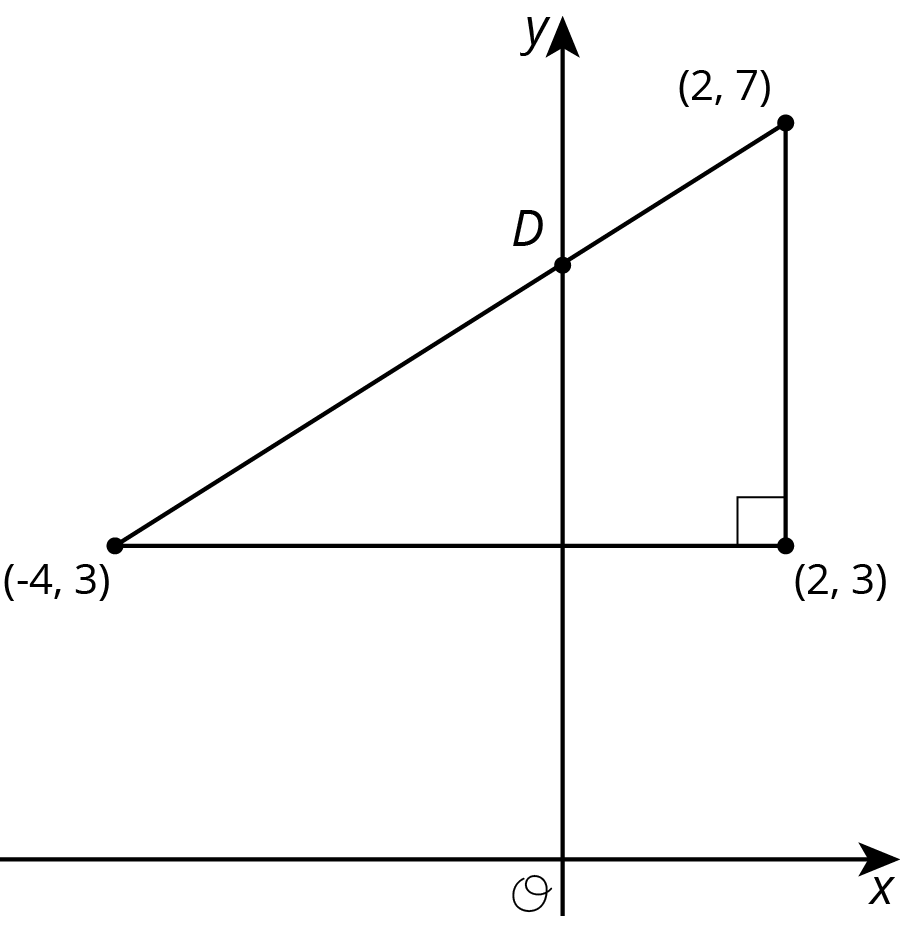
Solution
For access, consult one of our IM Certified Partners.
(From Unit 2, Lesson 16.)Problem 4
Solve each equation.
\(\frac17a+\frac34=\frac98\)
\(\frac23+\frac15b=\frac56\)
\(\frac32=\frac43c+\frac23\)
\(0.3d+7.9=9.1\)
\(11.03=8.78+0.02e\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 7.)