Lesson 14

Solving Systems of Equations

View Student Lesson

Problem 1

  1. Write equations for the lines shown.

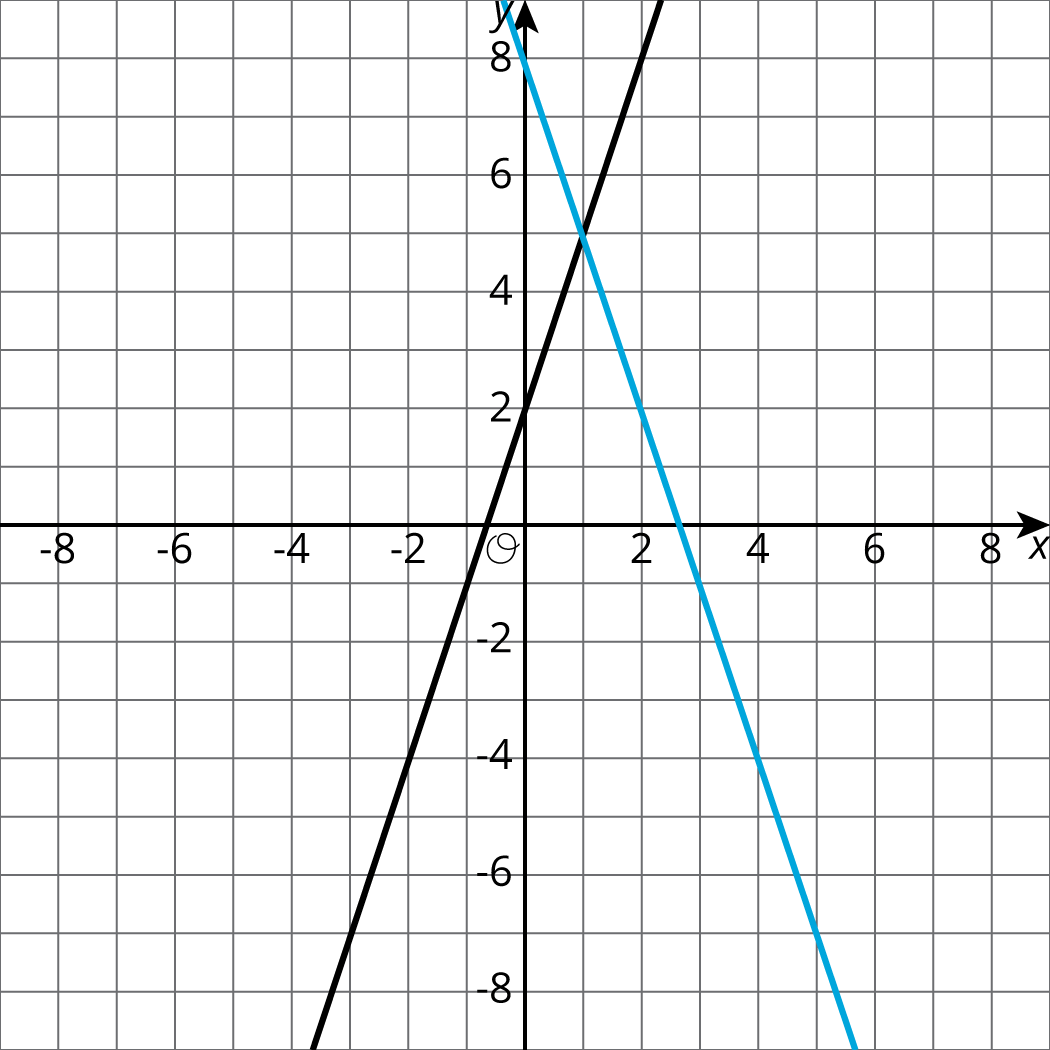
    Graph of two intersecting lines.

  2. Describe how to find the solution to the corresponding system by looking at the graph.
     

  3. Describe how to find the solution to the corresponding system by using the equations.
     

Solution

For access, consult one of our IM Certified Partners.

Problem 2

The solution to a system of equations is \((5, \text-19)\). Choose two equations that might make up the system.

A:

\(y = \text-3x - 6\)

B:

\(y = 2x - 23\)

C:

\(y = \text-7x + 16\)

D:

\(y = x -17\)

E:

\(y = \text-2x - 9\)

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Solve the system of equations: \(\begin{cases} y=4x-3 \\ y=\text-2x+9 \\ \end{cases}\)

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Solve the system of equations: \(\begin{cases} y=\frac54x-2 \\ y= \frac {\text{-}1}{4}x+19 \\ \end{cases}\)

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Here is an equation: \(\frac{15(x-3)}{5}= 3(2x-3)\)

  1. Solve the equation by using the distributive property first.
  2. Solve the equation without using the distributive property.
  3. Check your solution.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 14.)