Lesson 5
More Dilations
5.1: Many Dilations of a Triangle (5 minutes)
Warm-up
Students have seen many examples of scale factors that are less than and greater than 1, but the goal of this warm up is to have students focus explicitly on how the size of the scale factor impacts the dilation of a figure. Several dilations of one figure, with the same center but different scale factors, are displayed and students are asked to make observations about the shapes.
If using the digital activity, students will be able to scale a triangle by sliding the scale factor button. Students will informally make conjectures about the relationship between the original and scaled triangles. For example, the triangles are similar, the angles do not change, etc.
Launch
Show students the image from the task (or demonstrate the applet from the digital activity) and ask “What do you notice? What do you wonder?” Record their responses for all to see. Students may notice and wonder many things. Relevant mathematical things students may notice:
- There are triangles that look like dilations of each other.
- The center of dilation is point \(P\).
- The corresponding sides of the triangles are parallel to each other.
- There is a dashed line through each set of corresponding vertices.
- The corresponding angles appear to be congruent.
Things students may wonder:
- Which was the original triangle, and which are dilations of it?
- What scale factors were used?
Give students 2 minutes of quiet work time followed by a whole-class discussion.
Student Facing
Explore the applet and observe the dilation of triangle \(ABC\). The dilation always uses center \(P\), but you can change the scale factor. What connections can you make between the scale factor and the dilated triangle?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Show students the image from the task (or demonstrate the applet from the digital activity) and ask “What do you notice? What do you wonder?” Record their responses for all to see. Students may notice and wonder many things. Relevant mathematical things students may notice:
- There are triangles that look like dilations of each other.
- The center of dilation is point \(P\).
- The corresponding sides of the triangles are parallel to each other.
- There is a dashed line through each set of corresponding vertices.
- The corresponding angles appear to be congruent.
Things students may wonder:
- Which was the original triangle, and which are dilations of it?
- What scale factors were used?
Give students 2 minutes of quiet work time followed by a whole-class discussion.
Student Facing
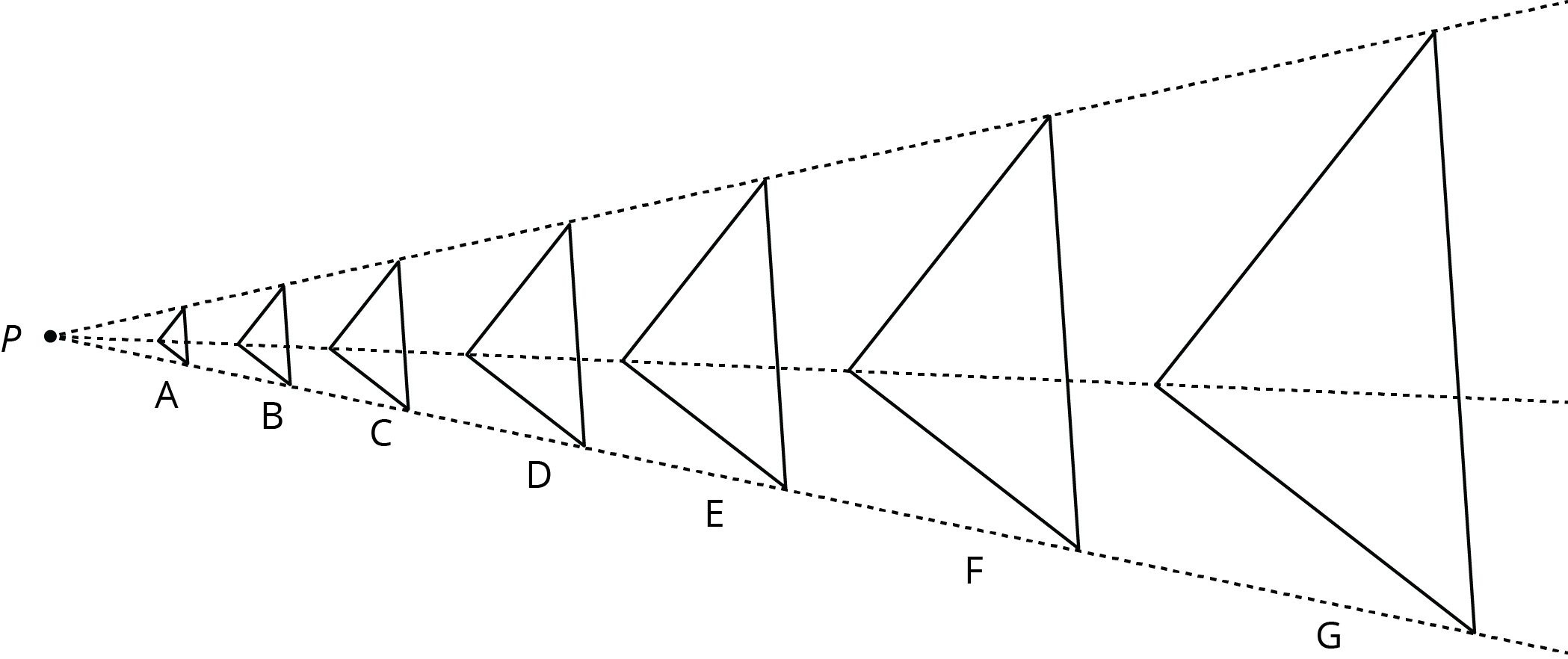
All of the triangles are dilations of Triangle D. The dilations use the same center \(P\), but different scale factors. What do Triangles A, B, and C have in common? What do Triangles E, F, and G have in common? What does this tell us about the different scale factors used?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students try to determine the actual scale factors between dilations, let them know that they only need to make an overall observation about the sizes of the dilations compared to Triangle D.
Activity Synthesis
Important observations include
- The smaller triangles come from scale factors less than one while the bigger triangles correspond to scale factors larger than one
- The original triangle, itself, can be seen as coming from a scale factor of one
- All of the triangles have the same angles and orientation in the plane
A few other points worth discussing include
- Any of these triangles is a dilation of any other with center \(P\).
- The lines from \(P\) contain “corresponding vertices” of the triangles (in the sense that these points map to one another via the dilations taking one triangle to another).
5.2: Info Gap: Dilations (20 minutes)
Activity
This info gap activity gives students an opportunity to determine and request the information needed for a dilation, and to realize that using coordinates greatly simplifies talking about specific points. In order to perform a dilation, students will need to know the center of dilation (which can be communicated using the coordinate grid), the coordinates of the polygon that they are dilating (also communicated using the coordinate grid), and the scale factor. With this information, they can find the dilation as in previous activities.
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for the information they need to solve the problem. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
Here is the text of one of the cards for reference and planning:
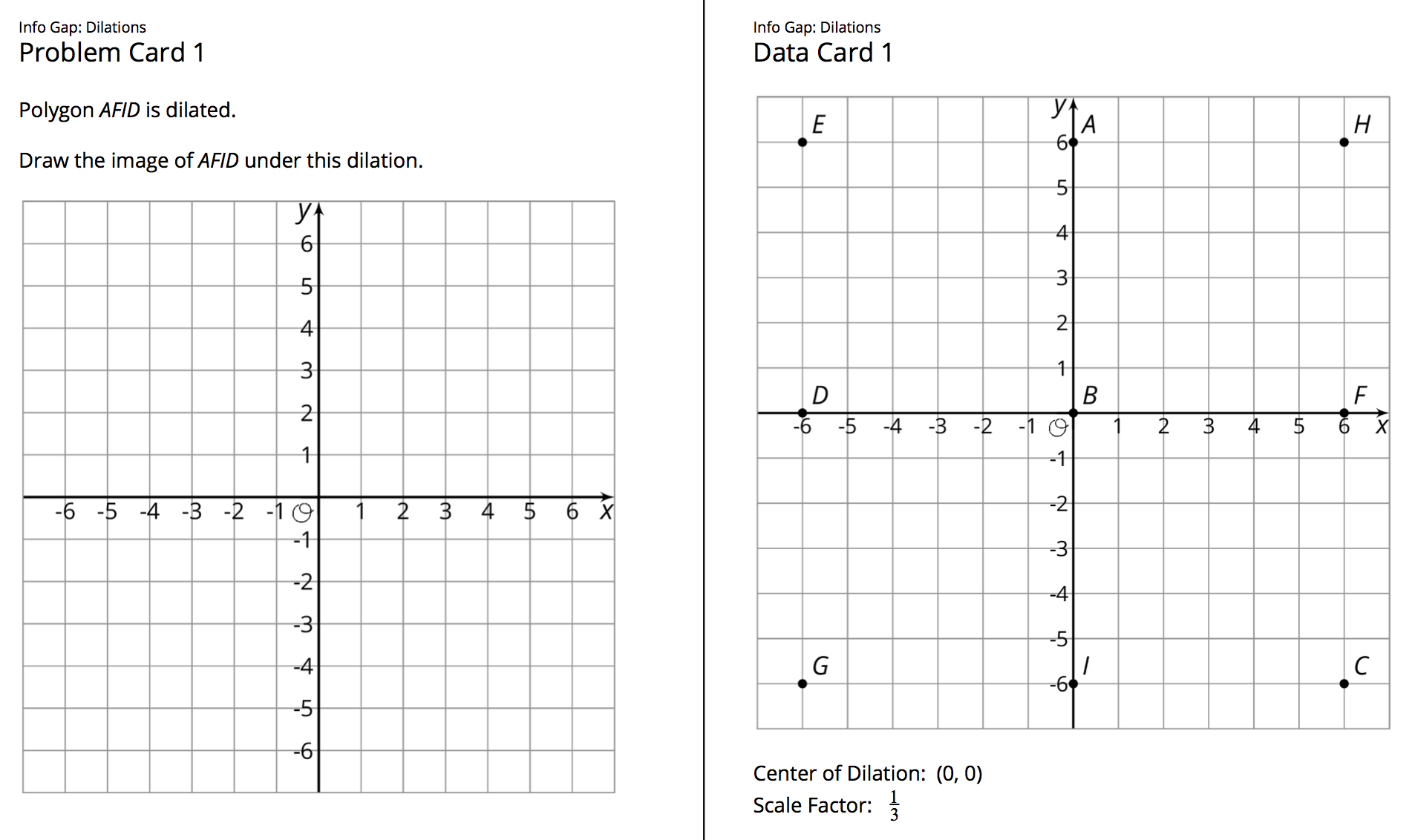
Listen for how students request (and supply) information about the center of dilation and the location of the polygon that is being dilated. The coordinate grid helps name and communicate the location of points, which is essential in this activity. In addition to the location of points, listen for how students use “center of dilation” and “scale factor” in order to communicate this essential information.
Launch
Tell students they will continue to practice describing and drawing dilations using coordinates. Explain the Info Gap and consider demonstrating the protocol if students are unfamiliar with it. Arrange students in groups of 2. Provide access to geometry toolkits. In each group, distribute a problem card to one student and a data card to the other student. After you review their work on the first problem, give them the cards for the second problem and instruct them to switch roles.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate Conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Triangle \(EFG\) was created by dilating triangle \(ABC\) using a scale factor of 2 and center \(D\). Triangle \(HIJ\) was created by dilating triangle \(ABC\) using a scale factor of \(\frac12\) and center \(D\).
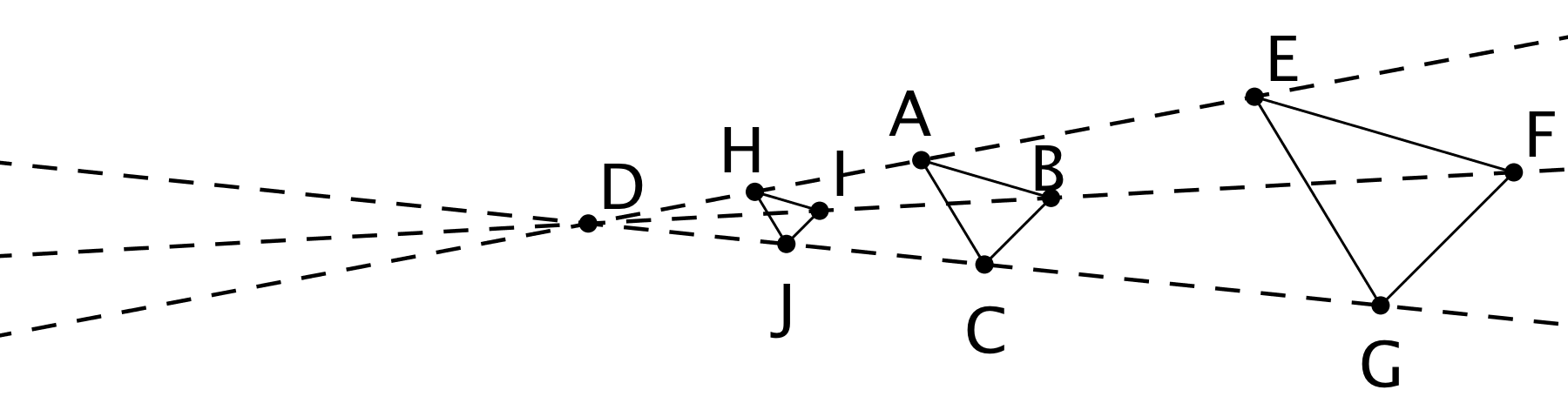
- What would the image of triangle \(ABC\) look like under a dilation with scale factor 0?
-
What would the image of the triangle look like under dilation with a scale factor of -1? If possible, draw it and label the vertices \(A’\), \(B’\), and \(C’\). If it’s not possible, explain why not.
-
If possible, describe what happens to a shape if it is dilated with a negative scale factor. If dilating with a negative scale factor is not possible, explain why not.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have completed their work, share the correct answers and ask students to discuss the process of solving the problems. Some guiding questions:
- “Other than the answer, what information would have been nice to have?”
- “How did using coordinates help in talking about the problem?”
- “If this same problem had a figure on a grid without coordinates, how would you talk about the points?”
- “What if there had been no grid at all? Would you still have been able to request or provide the needed information to perform the transformation?”
Highlight that coordinates allow us to unambiguously provide the location of a polygon’s vertices. In addition, reinforce the idea that in order to perform a dilation, we need to know the scale factor and the center of dilation. The coordinate grid again provides an efficient means to communicate the center of dilation.
Lesson Synthesis
Lesson Synthesis
Ask students to think about the question: “Why does anyone bother putting coordinate axes on a grid? Why are coordinates useful? What are they good for?”
Here are the points to emphasize: Coordinates are an exceptionally powerful tool for communicating the location of points in the plane. There is only one point 3 units to the left of the origin and 2 units up from the origin, the point \((\text-3, 2)\). The location of a polygon is determined by the location and order of its vertices. On a coordinate plane, these can be communicated by giving their coordinates. When we perform a dilation, we also need to know the center of dilation (another point) and the scale factor (a number). On the coordinate plane, all of the information we need to dilate a polygon can be communicated unambiguously with some numbers!
Coordinates in the plane are much like an address in the city: they tell you where to go unambiguously. Because the plane is laid out in a grid, these “addresses” are particularly simple, consisting of two signed numbers. We will use coordinates much more in this unit and beyond, not only to describe individual points but also to describe relationships (like proportional relationships and other new types of relationships).
5.3: Cool-down - Identifying a Dilation (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
One important use of coordinates is to communicate geometric information precisely. Let’s consider a quadrilateral \(ABCD\) in the coordinate plane. Performing a dilation of \(ABCD\) requires three vital pieces of information:
- The coordinates of \(A\), \(B\), \(C\), and \(D\)
- The coordinates of the center of dilation, \(P\)
- The scale factor of the dilation
With this information, we can dilate the vertices \(A\), \(B\), \(C\), and \(D\) and then draw the corresponding segments to find the dilation of \(ABCD\). Without coordinates, describing the location of the new points would likely require sharing a picture of the polygon and the center of dilation.