Lesson 5
More Dilations
Let’s look at dilations in the coordinate plane.
5.1: Many Dilations of a Triangle
Explore the applet and observe the dilation of triangle \(ABC\). The dilation always uses center \(P\), but you can change the scale factor. What connections can you make between the scale factor and the dilated triangle?
5.2: Info Gap: Dilations
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Triangle \(EFG\) was created by dilating triangle \(ABC\) using a scale factor of 2 and center \(D\). Triangle \(HIJ\) was created by dilating triangle \(ABC\) using a scale factor of \(\frac12\) and center \(D\).
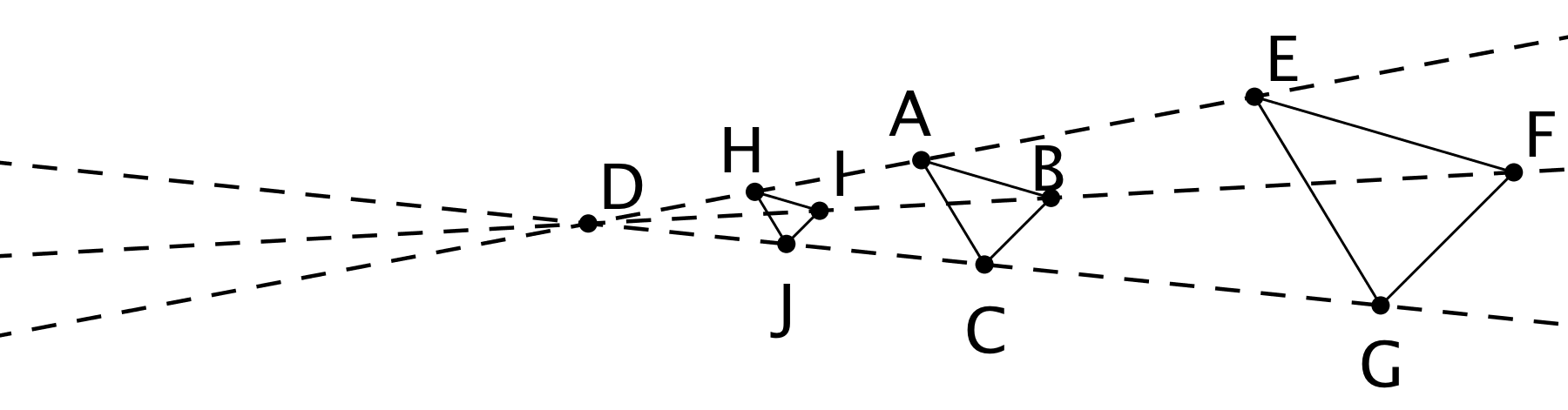
- What would the image of triangle \(ABC\) look like under a dilation with scale factor 0?
-
What would the image of the triangle look like under dilation with a scale factor of -1? If possible, draw it and label the vertices \(A’\), \(B’\), and \(C’\). If it’s not possible, explain why not.
-
If possible, describe what happens to a shape if it is dilated with a negative scale factor. If dilating with a negative scale factor is not possible, explain why not.
Summary
One important use of coordinates is to communicate geometric information precisely. Let’s consider a quadrilateral \(ABCD\) in the coordinate plane. Performing a dilation of \(ABCD\) requires three vital pieces of information:
- The coordinates of \(A\), \(B\), \(C\), and \(D\)
- The coordinates of the center of dilation, \(P\)
- The scale factor of the dilation
With this information, we can dilate the vertices \(A\), \(B\), \(C\), and \(D\) and then draw the corresponding segments to find the dilation of \(ABCD\). Without coordinates, describing the location of the new points would likely require sharing a picture of the polygon and the center of dilation.
Video Summary
Glossary Entries
- center of a dilation
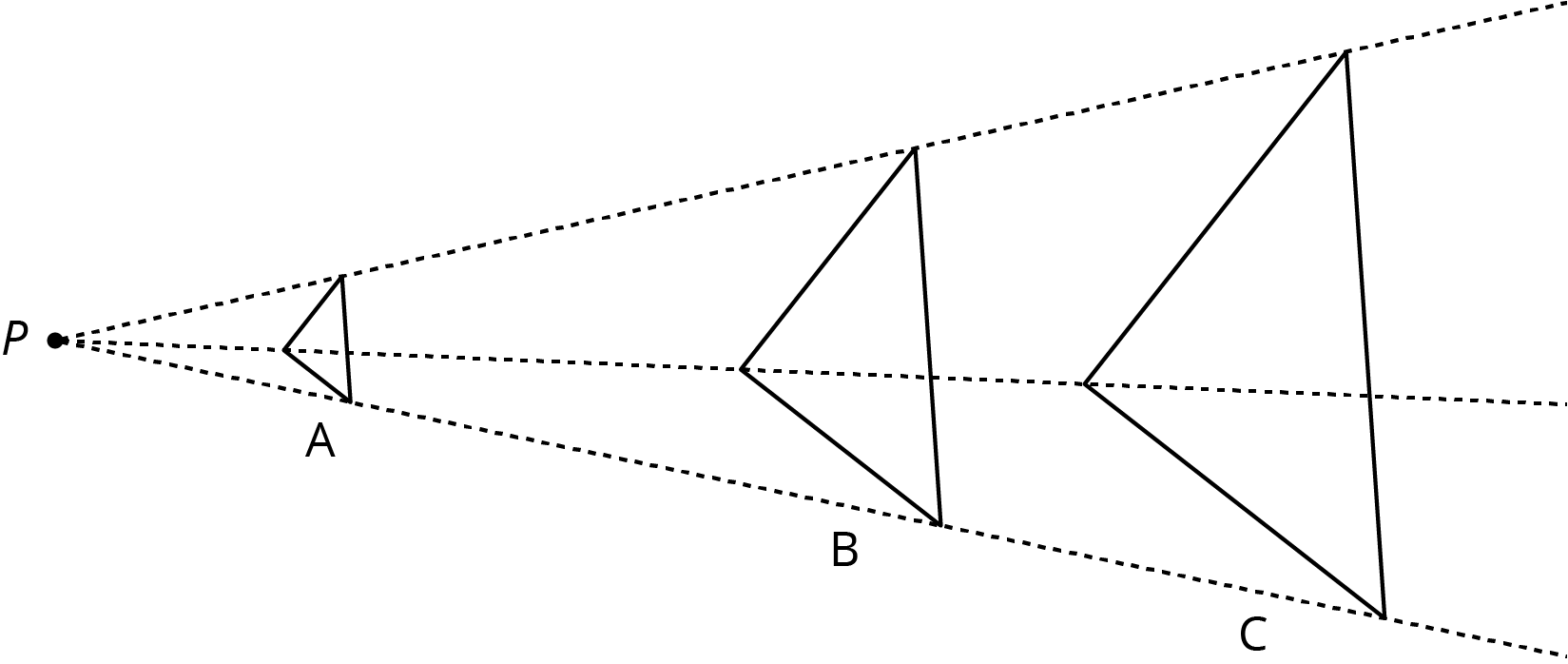
The center of a dilation is a fixed point on a plane. It is the starting point from which we measure distances in a dilation.
In this diagram, point \(P\) is the center of the dilation.
- dilation
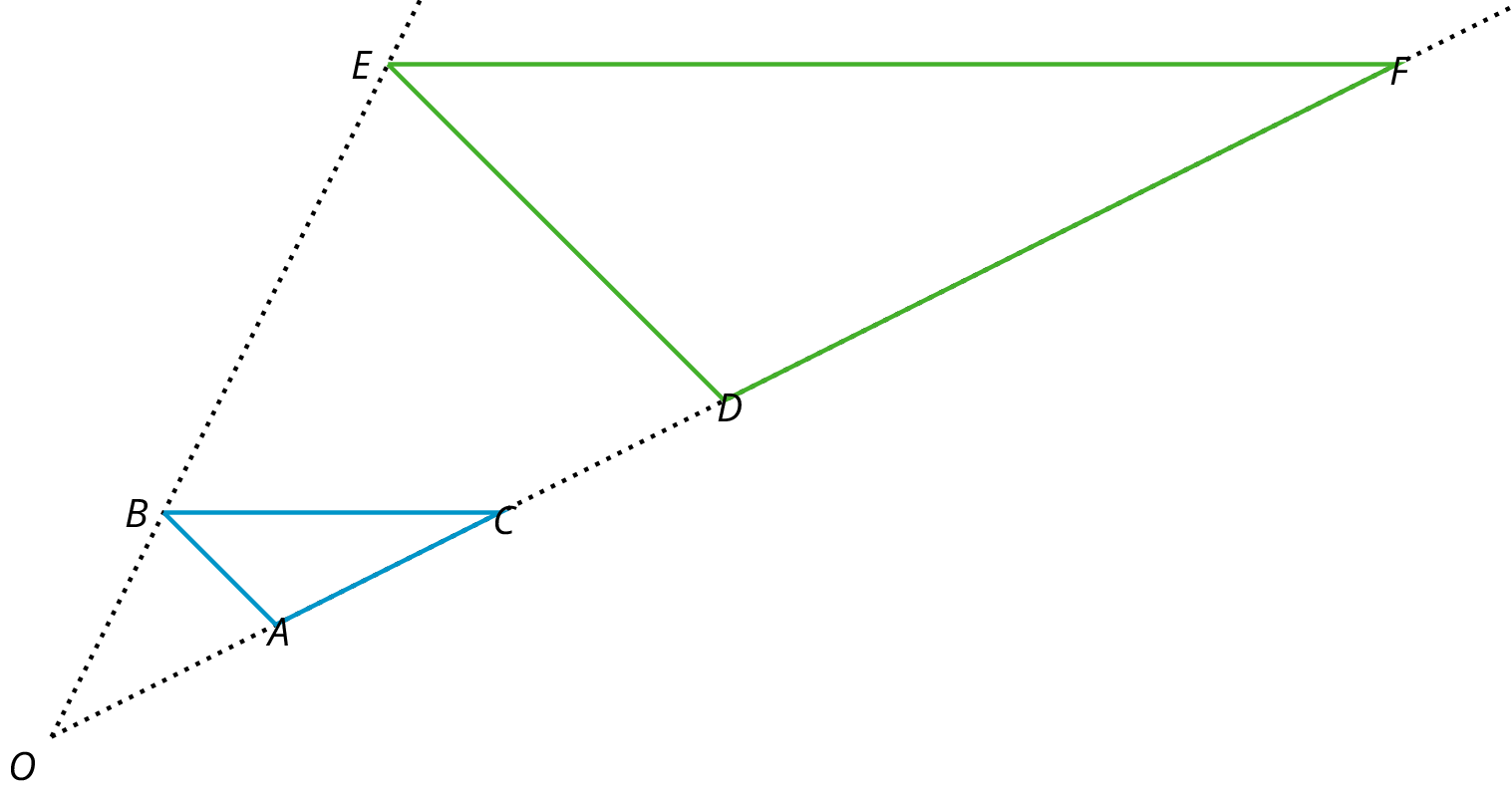
A dilation is a transformation in which each point on a figure moves along a line and changes its distance from a fixed point. The fixed point is the center of the dilation. All of the original distances are multiplied by the same scale factor.
For example, triangle \(DEF\) is a dilation of triangle \(ABC\). The center of dilation is \(O\) and the scale factor is 3.
This means that every point of triangle \(DEF\) is 3 times as far from \(O\) as every corresponding point of triangle \(ABC\).
- scale factor
To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.
In this example, the scale factor is 1.5, because \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).
