Lesson 3
Dilations with no Grid
3.1: Points on a Ray (5 minutes)
Warm-up
Students apply a dilation to points on a ray. The scaffold of the circular grid has been removed but the structure of dilations is the same.
Without the grid, students will need to come up with a way to measure in order to find the point twice as far from \(A\) as \(B\) and half as far from \(A\) as \(B\). They can use a ruler or the edge of an index card.
Monitor for these methods:
- using a ruler to measure distances
- marking off distances on an index card (for problem 1)
- folding paper in half (for problem 2)
Select students who use these methods and invite them to present.
Launch
Provide access to geometry toolkits.
Student Facing
- Find and label a point \(C\) on the ray whose distance from \(A\) is twice the distance from \(B\) to \(A\).
- Find and label a point \(D\) on the ray whose distance from \(A\) is half the distance from \(B\) to \(A\).
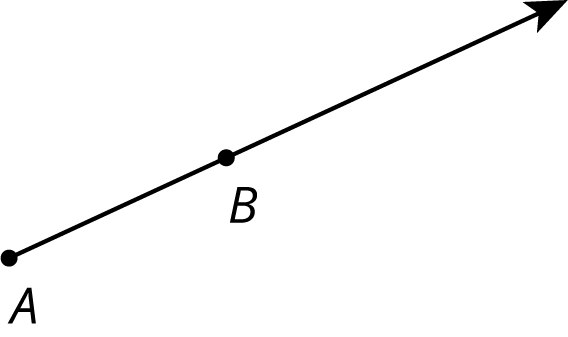
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to present their methods for finding the points which may include:
- using a ruler to measure distances
- marking off distances on an index card (for problem 1)
- folding paper in half (for problem 2)
Point out how this is similar to work with dilations on a circular grid (the points lie on the same ray at different distances) and how it is different (there are no marked distances). For the next activity, it is important for students to understand that \(C\) is the dilation of \(B\) with center \(A\) and scale factor 2. And \(D\) is the dilation of \(B\) with center \(A\) and scale factor \(\frac{1}{2}\).
3.2: Dilation Obstacle Course (10 minutes)
Activity
This activity investigates dilations with no grid. Students have seen these for the first time in the warm-up, which had a ray drawn between two points. That scaffold has been removed here so the teacher may need to provide guidance by suggesting that students draw appropriate rays.
Encourage students to measure distances carefully at first, since the problem statement does not state that the image of each point, after the dilation indicated, is one of the labeled points. After doing a few of the problems, the students should notice that the dilated point is always one of the labeled points and then use this observation to expedite the work. Also monitor for students who see the relationship between the scale factors used to send \(G\) to \(E\) and \(E\) to \(G\) (both with center \(H\)).
Launch

If using the digital activity, it may be easiest for students to work with a partner, with one device used to manipulate the applet and the other device used to display the questions.
Supports accessibility for: Organization; Attention
Student Facing
-
Dilate \(B\) using a scale factor of 5 and \(A\) as the center of dilation. Which point is its image?
-
Using \(H\) as the center of dilation, dilate \(G\) so that its image is \(E\). What scale factor did you use?
-
Using \(H\) as the center of dilation, dilate \(E\) so that its image is \(G\). What scale factor did you use?
-
To dilate \(F\) so that its image is \(B\), what point on the diagram can you use as a center?
-
Dilate \(H\) using \(A\) as the center and a scale factor of \(\frac{1}{3}\). Which point is its image?
-
Describe a dilation that uses a labeled point as its center and that would take \(F\) to \(H\).
-
Using \(B\) as the center of dilation, dilate \(H\) so that its image is itself. What scale factor did you use?
Student Response
For access, consult one of our IM Certified Partners.
Launch

If using the digital activity, it may be easiest for students to work with a partner, with one device used to manipulate the applet and the other device used to display the questions.
Supports accessibility for: Organization; Attention
Student Facing
Here is a diagram that shows nine points.

- Dilate \(B\) using a scale factor of 5 and \(A\) as the center of dilation. Which point is its image?
- Using \(H\) as the center of dilation, dilate \(G\) so that its image is \(E\). What scale factor did you use?
- Using \(H\) as the center of dilation, dilate \(E\) so that its image is \(G\). What scale factor did you use?
- To dilate \(F\) so that its image is \(B\), what point on the diagram can you use as a center?
- Dilate \(H\) using \(A\) as the center and a scale factor of \(\frac{1}{3}\). Which point is its image?
- Describe a dilation that uses a labeled point as its center and that would take \(F\) to \(H\).
- Using \(B\) as the center of dilation, dilate \(H\) so that its image is itself. What scale factor did you use?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might need to be reminded that the image of a point under dilation must lie on the same line as the point being dilated and the center of dilation. Students might think that for a point to be a dilation of itself, the scale factor is 0. If this happens, ask them to consider multiplying the distance of the point by 0. (If they want the distance to be the same, they actually need to multiply it by 1 instead.)
Activity Synthesis
Discuss any strategies used to solve the problems. Ask selected students who noticed that the answers to all of the questions were labeled points to share their observation and how it helped them answer the questions. Next ask selected students to share their observation about the scale factors for dilating \(G\) to \(E\) and dilating \(E\) back to \(G\). One way to reverse or “undo” a dilation is to use the same center and reciprocal scale factor.
Other important ideas to bring out include:
- The center of dilation, the point being dilated, and the image of the point after dilation must all lie on the same line.
- A scale factor of 1 does not move any points. If the scale factor is not 1, only one point does not move (the center of dilation).
Design Principle(s): Support sense-making
3.3: Getting Perspective (15 minutes)
Activity
In this activity, students continue to apply dilations without a grid. Unlike in the previous activity, the dilated images of the points are not plotted. So rather than identifying the correct point, they will need to find an appropriate way to take measurements (MP5), most likely with the aid of a ruler or the edge of an index card. Different students will work with different scale factors and will produce perspective drawings of a box.
Watch for students who pick a point close to one vertex of the given rectangle. If the point is too close, it will be more difficult to visualize the box. Suggest that they move the point further away. Monitor for students who produce accurate drawings with different scale factors and invite them to share during the discussion.
Launch
Provide access to geometry toolkits.
First, a demonstration about dilating a point on a plane with no grid.

We want to dilate point \(B\) using \(A\) as the center of dilation and a scale factor of 3.
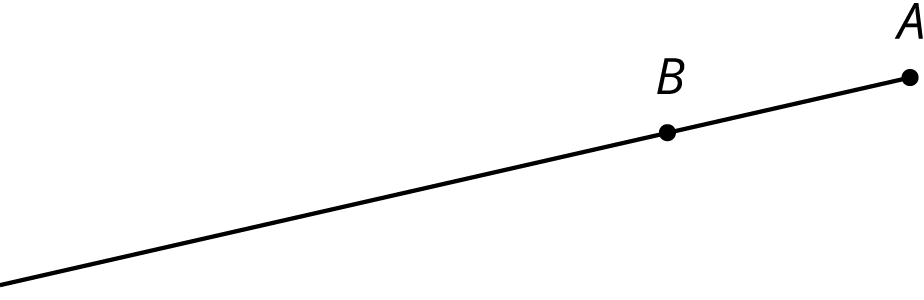
Use a straightedge to draw ray \(AB\).
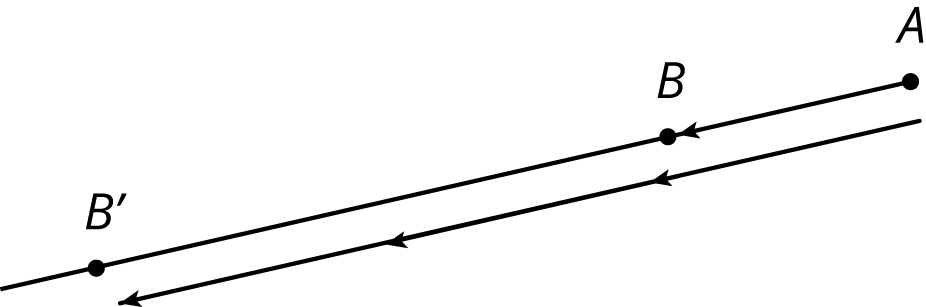
Measure the distance from \(B\) to \(A\). Multiply the distance by 3. Draw \(B’\) so that it is 3 times as far away from \(A\). For scale factors that are integers, an unmarked edge of an index card or a compass can also be used to transfer the distance along the ray.
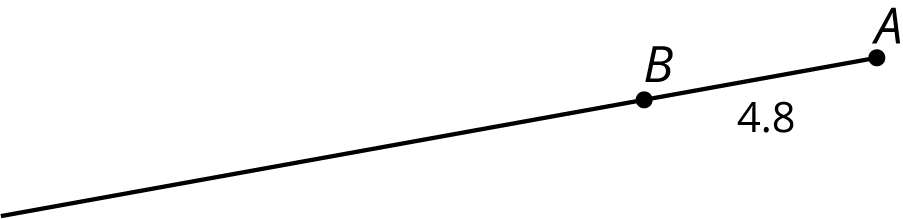
If we wanted a scale factor that is not an integer the procedure is the same. Measure the distance from \(A\) to \(B\), multiply by the scale factor, and place \(B’\) at that new distance from \(A\).
Let’s say the distance from \(A\) to \(B\) is 4.8 cm.
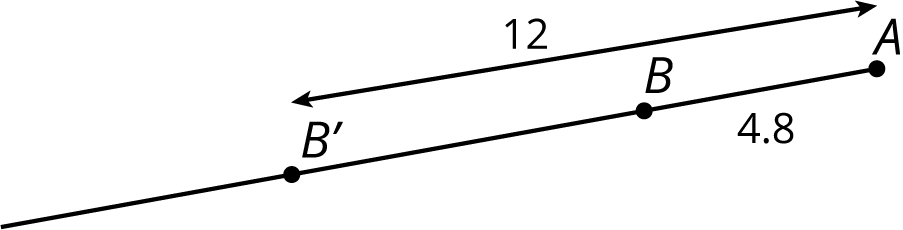
If we wanted to use a scale factor of 2.5, the distance from \(A\) to the dilated point \(B’\) would be 12 cm, because \((4.8) \boldcdot (2.5) = 12\).
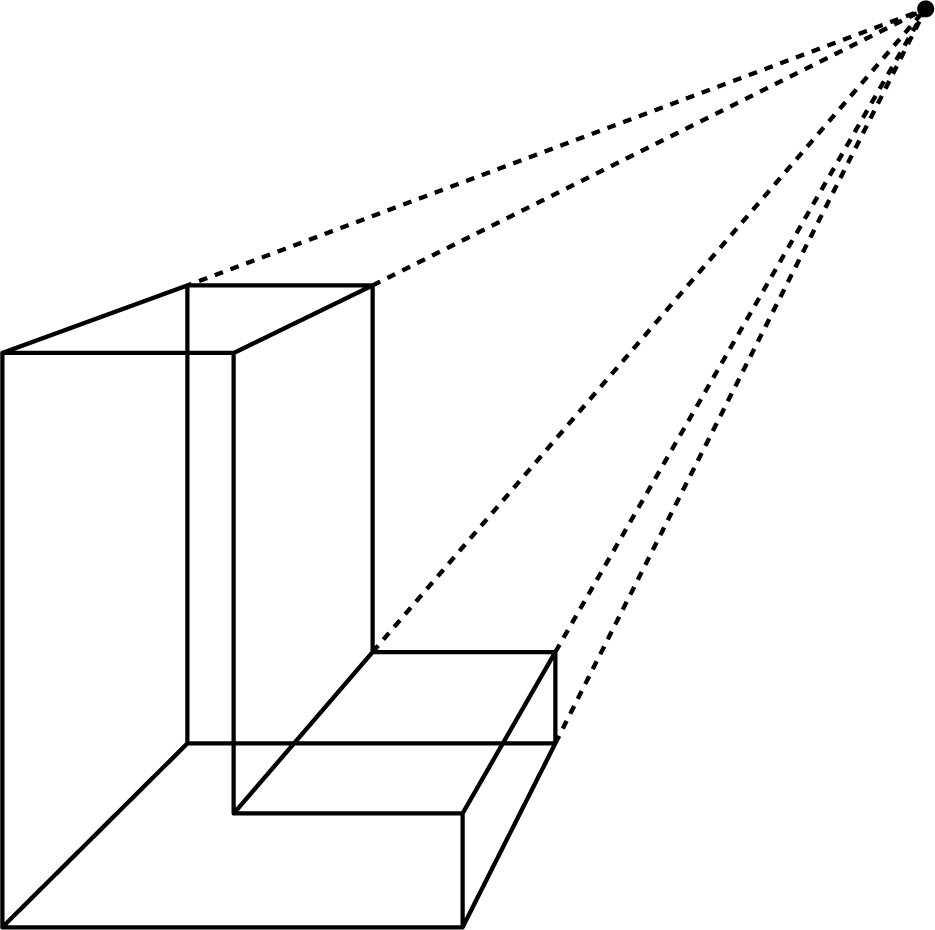
A perspective drawing is an optical illusion that makes an image printed on paper have a three-dimensional look. Display at least one example of a perspective drawing:
Students will practice some simple dilations of points, and then they will create a perspective drawing. Tell students to complete the first part of the activity dilating points \(P\) and \(Q\). After you review their work, assign each student a scale factor to use for the second part. Appropriate scale factors include \(\frac{1}{3}\), \(\frac{1}{2}\), \(1\frac{1}{2}\), and 2. It will work best if the center of the dilation is not too close to the rectangle the students are dilating.
Supports accessibility for: Language; Memory
Student Facing
- Dilate \(P\) using \(C\) as the center and a scale factor of 4. Follow the directions to perform the dilations in the applet.
- Select the Dilate From Point tool.
- Click on the object to dilate, and then click on the center of dilation.
- When the dialog box opens, enter the scale factor. Fractions can be written with plain text, ex. 1/2.
- Click

- Use the Ray tool and the Distance tool to verify.
- Select the Dilate From Point tool.
-
Dilate \(Q\) using \(C\) as the center and a scale factor of \(\frac12\).
-
Draw a simple polygon.
- Choose a point outside the polygon to use as the center of dilation. Label it \(C.\)
- Using your center \(C\) and the scale factor you were given, draw the image under the dilation of each vertex of the polygon, one at a time. Connect the dilated vertices to create the dilated polygon.
- Draw a segment that connects each of the original vertices with its image. This will make your diagram look like a cool three-dimensional drawing of a box! If there's time, you can shade the sides of the box to make it look more realistic.
- Compare your drawing to other people’s drawings. What is the same and what is different? How do the choices you made affect the final drawing? Was your dilated polygon closer to \(C\) than to the original polygon, or farther away? How is that decided?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Provide access to geometry toolkits.
First, a demonstration about dilating a point on a plane with no grid.

We want to dilate point \(B\) using \(A\) as the center of dilation and a scale factor of 3.
Use a straightedge to draw ray \(AB\).

Measure the distance from \(B\) to \(A\). Multiply the distance by 3. Draw \(B’\) so that it is 3 times as far away from \(A\). For scale factors that are integers, an unmarked edge of an index card or a compass can also be used to transfer the distance along the ray.

If we wanted a scale factor that is not an integer the procedure is the same. Measure the distance from \(A\) to \(B\), multiply by the scale factor, and place \(B’\) at that new distance from \(A\).
Let’s say the distance from \(A\) to \(B\) is 4.8 cm.

If we wanted to use a scale factor of 2.5, the distance from \(A\) to the dilated point \(B’\) would be 12 cm, because \((4.8) \boldcdot (2.5) = 12\).
A perspective drawing is an optical illusion that makes an image printed on paper have a three-dimensional look. Display at least one example of a perspective drawing:

Students will practice some simple dilations of points, and then they will create a perspective drawing. Tell students to complete the first part of the activity dilating points \(P\) and \(Q\). After you review their work, assign each student a scale factor to use for the second part. Appropriate scale factors include \(\frac{1}{3}\), \(\frac{1}{2}\), \(1\frac{1}{2}\), and 2. It will work best if the center of the dilation is not too close to the rectangle the students are dilating.
Supports accessibility for: Language; Memory
Student Facing
- Using one colored pencil, draw the images of points \(P\) and \(Q\) using \(C\) as the center of dilation and a scale factor of 4. Label the new points \(P’\) and \(Q’\).
-
Using a different color, draw the images of points \(P\) and \(Q\) using \(C\) as the center of dilation and a scale factor of \(\frac12\). Label the new points \(P’’\) and \(Q’’\).

Pause here so your teacher can review your diagram. Your teacher will then give you a scale factor to use in the next part. -
Now you’ll make a perspective drawing. Here is a rectangle.

-
Choose a point inside the shaded circular region but outside the rectangle to use as the center of dilation. Label it \(C\).
-
Using your center \(C\) and the scale factor you were given, draw the image under the dilation of each vertex of the rectangle, one at a time. Connect the dilated vertices to create the dilated rectangle.
-
Draw a segment that connects each of the original vertices with its image. This will make your diagram look like a cool three-dimensional drawing of a box! If there’s time, you can shade the sides of the box to make it look more realistic.
-
Compare your drawing to other people’s drawings. What is the same and what is different? How do the choices you made affect the final drawing? Was your dilated rectangle closer to \(C\) than to the original rectangle, or farther away? How is that decided?
-
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Here is line segment \(DE\) and its image \(D’E’\) under a dilation.
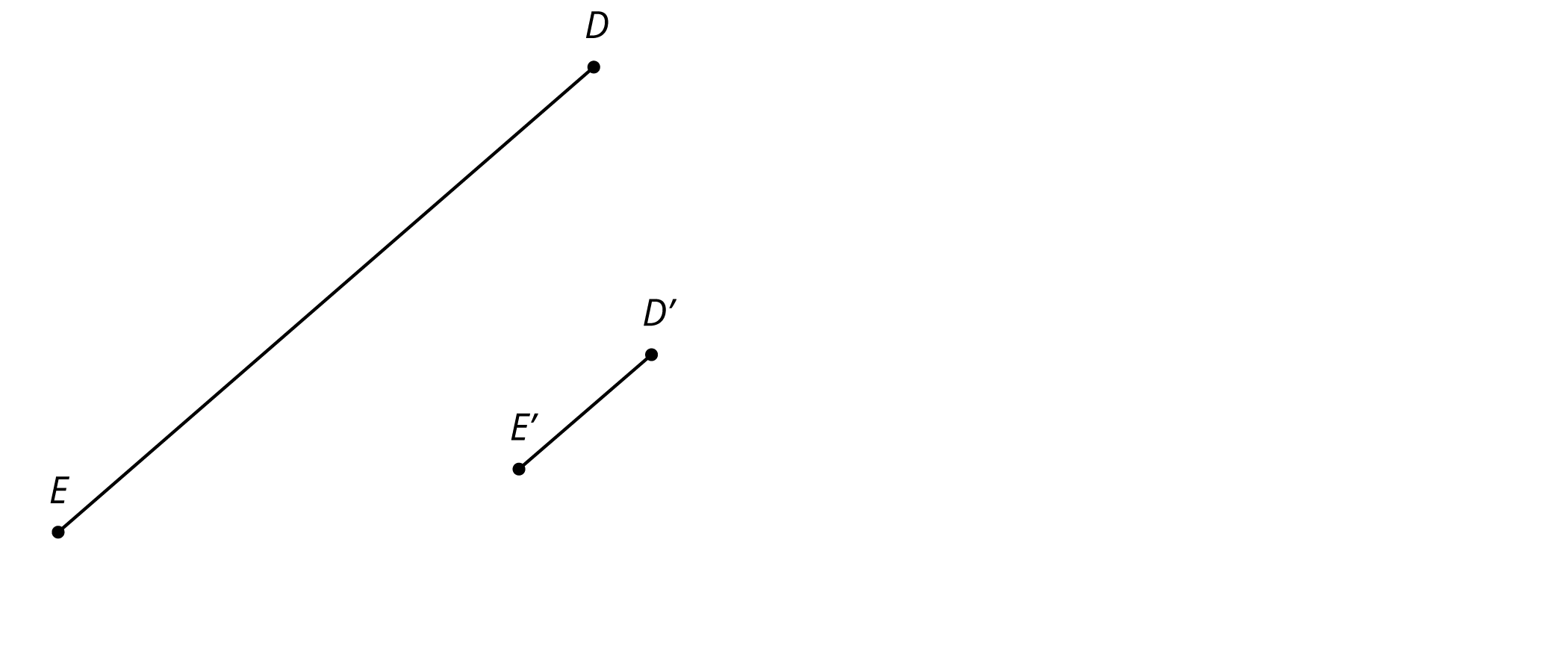
- Use a ruler to find and draw the center of dilation. Label it \(F\).
- What is the scale factor of the dilation?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may all try to make their drawing match any example drawings shown in the launch. For example, if the center of dilation in an example is above and to the right, everyone might place their center of dilation above and to the right of the rectangle. Any point is fine as a dilation point, but the effect on what the picture looks like may vary.
Students may not recall that to dilate a polygon, they can first dilate the vertices and then connect them in the proper order. It may be necessary to show students how to dilate one of the vertices and allow them to perform the dilation on the other three vertices.
Activity Synthesis
Display the work of several students selected based on the different scale factors. Then ask students:
- “What are the effects of using a scale factor greater than 1?” (The image is larger than the original and farther away from the center of dilation than the original.)
- “What are the effects of using a scale factor less than 1?” (The image is smaller than the original and closer to the center of dilation than the original.)
- “What effect does the location of \(C\), the center of dilation, have?” (It impacts the size and location of the dilated rectangle: if the scale factor is less than 1 then the dilated rectangle is closer to \(C\) than the original and if the scale factor is larger than 1 then the dilated rectangle is further away from \(C\) than the original.)
Time permitting, consider showing several student drawings with the same scale factor but a different location for the point \(C\). How are they the same? How are they different? Two faces of these boxes (the original rectangle and the scaled copy) are congruent but the point of view or perspective on them is different.
Design Principles(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Ask students to think about how they would explain the steps for dilating a point, and either write them down or share them with a partner. Ask a few students to share their steps. Ensure that all of the important aspects are mentioned:
- “You need to know which point you want to dilate, which point is the center of dilation, and what scale factor to use.”
- “Use a straightedge to draw a ray from the center of dilation through the point you want to dilate.”
- “Measure the distance from the center of dilation through the point. Multiply this distance by the scale factor. Place the new point at this distance from the center of dilation and also on the ray you drew.”
- “If the scale factor is greater than 1, the new point will be farther from the center than the original point. If the scale factor is less than 1, the new point will be closer to the center than the original point.”
3.4: Cool-down - A Single Dilation of a Triangle (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
If \(A\) is the center of dilation, how can we find which point is the dilation of \(B\) with scale factor 2?

A dilation with scale factor less than 1 brings points closer. The point \(D\) is the dilation of \(B\) with center \(A\) and scale factor \(\frac{1}{3}\).