Lesson 13
The Shadow Knows
13.1: Notice and Wonder: Long Shadows and Short Shadows (5 minutes)
Warm-up
The purpose of this warm-up is to show what happens when shadows are cast from a lamp versus the Sun. Later in this lesson, it is important that students understand that rays of sunlight that hit Earth are essentially parallel. While students may notice and wonder many things about these images, the length of the shadows (which are different for the pens near the lamp and appear to be same for the pens in the sunshine) is the most important discussion point.
The rest of this lesson will look at the shadows of the pens (and other objects) in detail, using the idea that the rays of sunlight hitting the pens are parallel (or nearly so).
Launch
Arrange students in groups of 2. 2 minutes of quiet think time then share with a partner.
Student Facing
What do you notice? What do you wonder?


Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. After each response, ask the class if they agree or disagree and to explain alternative ways of thinking, referring back to the images each time.

If possible, show these images where the path of the light that reaches the top of each shadow is drawn in.
Use MLR 2 (Collect and Display) to gather words and phrases students use when describing why the pens do not have the same length of shadows in the first picture but do in the second. Make explicit connections to illustrate that the Sun’s light hits the pens at the same angle.
13.2: Objects and Shadows (15 minutes)
Activity
In this activity, students look at a photo of three people, a lamppost, and their shadows taken on a sunny day. They notice that there is an approximately proportional relationship between the height of an object and the length of its shadow. Then, they use what they know about proportional relationships and the length of a shadow to find the height of an object that is difficult to measure directly.
In this activity, students just notice that the relationship appears to be proportional based on inspecting several corresponding lengths. In the next activity, they will create a justification for why the relationship is proportional.
The given measurements are real measurements rounded to the nearest inch. Therefore, the given values are not in a perfectly proportional relationship. The quotient of each shadow length and its corresponding object’s height is around, but not exactly, \(\frac23\). Students are engaging in MP4 when they reason mathematically about real-world measurements.
Launch
Display the photo in the task, and ask students how they would go about measuring the height of each person and the lamppost. It would be straightforward to measure the height of the people using a yard stick or tape measure, but it would be difficult to measure the height of the lamppost. Tell students that even when something is too tall to measure directly, we can still figure out its height by using the length of its shadow (which, since it's on the ground, is easy to measure).
Draw students’ attention to the measurements given in the table, and invite students to look for relationships in the table and use any relationships they notice to make a conjecture about the height of the lamppost.
Keep students in the same groups. 2 minutes of quiet work time and then students share thinking and continue working with a partner, followed by a whole-class discussion.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Design Principle(s): Support sense-making, Maximize meta-awareness
Student Facing

Here are some measurements that were taken when the photo was taken. It was impossible to directly measure the height of the lamppost, so that cell is blank.
| height (inches) | shadow length (inches) | |
|---|---|---|
| younger boy | 43 | 29 |
| man | 72 | 48 |
| older boy | 51 | 34 |
| lamppost | 114 |
-
What relationships do you notice between an object’s height and the length of its shadow?
-
Make a conjecture about the height of the lamppost and explain your thinking.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The task uses real measurements that were taken to the nearest inch. Because of the rounding, the values given are not in a perfectly proportional relationship, so students may hesitate to identify the relationship as proportional. If students struggle with this aspect of the activity, suggest that they start by coming up with a range of reasonable values for the height of the post. Also, share with them that the measurements were rounded to the nearest inch, so it’s possible that the relationship is imperfect.
Some students may need help understanding the meaning of “conjecture.” A simple definition to use is “a reasonable guess.”
Activity Synthesis
Students should notice that the relationship appears to be approximately proportional. Highlight that the height to shadow length relationship is not exactly proportional because, for example, \(\frac{43}{29}\) and \(\frac{72}{48}\) are not equal (though they are very close). This could be because of rounding error in the measurements or other factors that make the real world differ slightly from a mathematical model. It may be interesting for students to speculate on some reasons (for example, perhaps the ground is not perfectly level, or perhaps one of the people or the lamppost is at a slightly different angle to the ground), though the next activity provides ample opportunity to discuss them, too.
If any students decide to create a graph of the associated heights and shadow lengths, it looks like this (or may have the axes reversed).
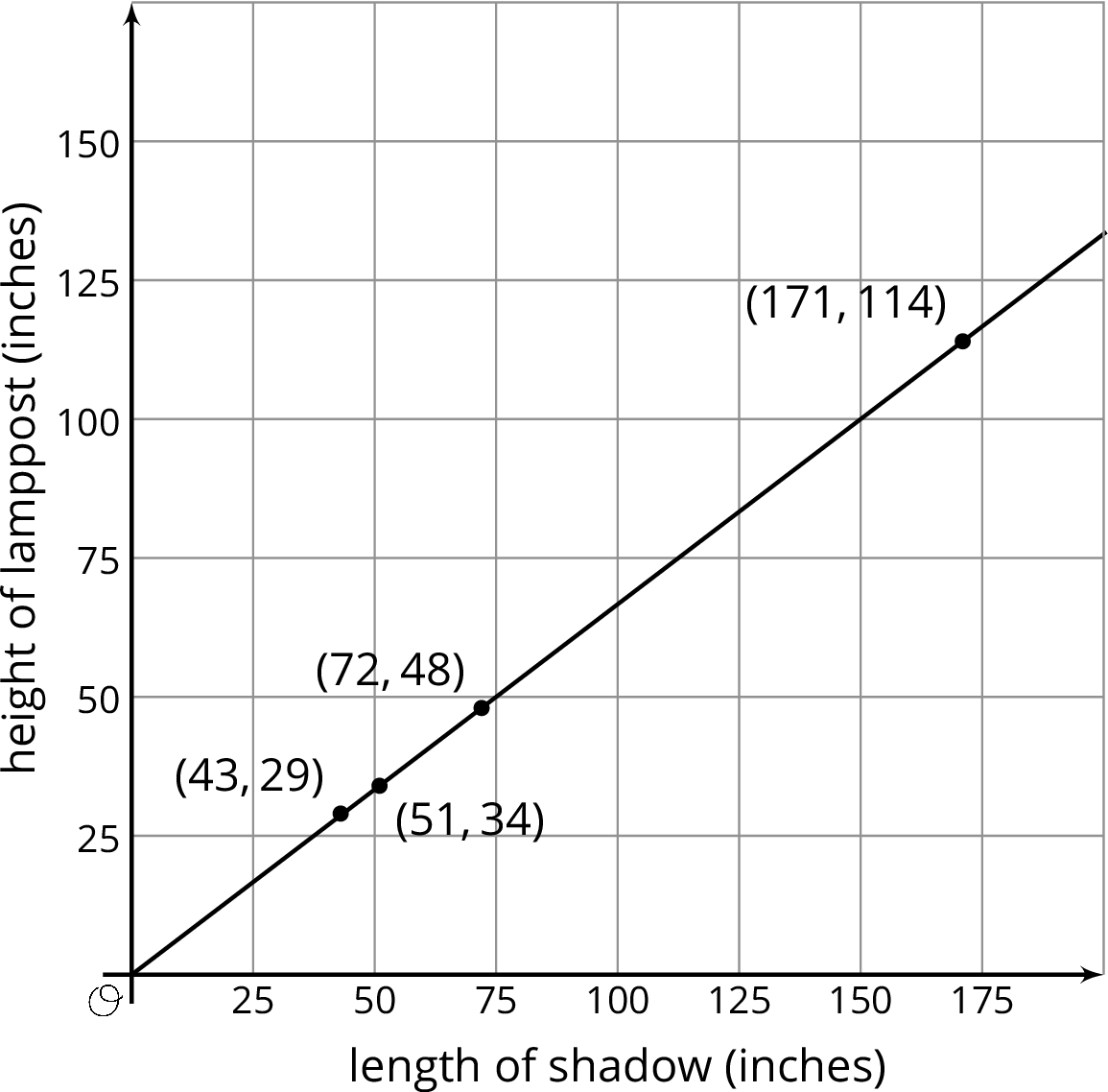
13.3: Justifying the Relationship (15 minutes)
Activity
The purpose of this activity is for students to write a mathematical justification for the proportional relationship between heights and shadow lengths in the photo. A version of the photo is provided with some line segments drawn to strongly suggest an argument based on similar triangles. Given the work they have done up to this point, it is likely that students will recognize that similar triangles will be part of their justification. Many students need help understanding what components are important to include in their arguments. The more that students do on their own, the more fully they are engaging in MP1 and MP3.
Because the Sun is so very far away relative to its size, the rays that reach Earth are extremely close to parallel. This is essential in the argument, and you may decide to share this information with the students or ask them to think about the shadows of the pens in the warm-up. The prompt asks to show that the relationship is approximately proportional, leaving room for the fact that the Sun’s rays may not be exactly parallel, or one of the people is not standing precisely perpendicular to the ground, or the ground may not be perfectly level. Stating and using simplifying assumptions is a good example of MP4.
Launch
Keep students in the same groups. From the previous activity, the shadow measurements make us suspect there may be a proportional relationship between the object heights and the shadow lengths. Tell students that their goal here is to justify why the relationship is (approximately) proportional.
Student Facing
Explain why the relationship between the height of these objects and the length of their shadows is approximately proportional.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students often struggle with deciding what is important to include in their explanation. A useful technique is to think about what you want to show, and then asking a series of questions. In this activity, we want to show that there is a proportional relationship between the side lengths in some triangles. Questions could include, “What types of triangles have sides that are in proportion? How do you know when triangles are similar triangles? Which pairs of angles do you know are congruent? Why are they congruent?” The answers to these questions are the building blocks of an argument.
Activity Synthesis
Debrief as a class. Invite selected students to share their explanations. Ask other students to restate, support, refine, or disagree with their arguments.
Emphasize that it is often necessary to make simplifying assumptions when modeling a real-world situation. For this geometric argument to work, for example, we have to assume that the light rays coming from the Sun are parallel, that the people and the lamppost are perpendicular to the ground, and that the ground is level.
Supports accessibility for: Attention; Social-emotional skills
Design Principles(s): Optimize output (for explanation); Maximize meta-awareness
13.4: The Height of a Tall Object (20 minutes)
Activity
This activity could be done on a sunny day. You should try it out ahead of time to ensure that the shadows created in your part of the world at the time your class takes place are cooperative! Either find a tall object outside that all students will find the height of, or let students choose a tall object (for example: a flagpole, a building, or a tree). It should be tall enough that its height can’t be easily measured directly, on level ground, and perpendicular to the ground. Students head outside with tape measures (or other measuring devices) and use what they’ve learned in this lesson to figure out the height of the tall object.
This is a modeling task (MP4) as the goal of the task is to solve a real-world problem (find the height of some object), and students need to devise and justify a method to do this. They have developed the tools in this lesson but need to apply them appropriately.
Launch
Tell students that they are going to apply what they have learned about shadow lengths of different objects to estimate the height of an object outside. Either tell them which object to use or explain the parameters for choosing an appropriate object.
Students require tape measures, yardsticks, or rulers, and a way to record their measurements. 5–10 minutes to take measurements and do calculations followed by a whole-class discussion.
Supports accessibility for: Attention; Social-emotional skills
Student Facing
-
Head outside. Make sure that it is a sunny day and you take a measuring device (like a tape measure or meter stick) as well as a pencil and some paper.
-
Choose an object whose height is too large to measure directly. Your teacher may assign you an object.
-
Use what you have learned to figure out the height of the object! Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The main technique that students will apply to solve this problem is likely proportional reasoning. Make sure to highlight the explanation for why the relationship is proportional uses angles made by parallel lines cut by a transversal (studied in the previous unit) and properties of similar triangles (a focus of this unit).
Students may think of the height of the object and the length of its shadow as a pair \((x,y)\) lying on a line whose slope is known. They know the shadow length and are looking for the corresponding height. While this line of reasoning could be considered grade 7 work, students now have the new language of slope (in addition to unit rate and constant of proportionality) to use in these calculations.
Lesson Synthesis
Lesson Synthesis
The activities in this lesson are a good example of using mathematics to model a real-world situation.
- The data is not always perfect (in this case, the object height to shadow length relationship was only approximately proportional).
- To explain why the object height to shadow length relationship might be proportional, simplifying assumptions were needed.
- Mathematical models can be used to make accurate guesses or predictions about quantities that are difficult or impossible to measure directly. In this case, a relationship between the height of an object and the length of its shadow was observed from easier-to-get measurements and justified by reasoning about similar triangles. Once we knew this relationship existed and why it existed, we could reasonably expect the same relationship to hold for a very tall object nearby at the same time of day, and use the length of the tall object's shadow to find its height.
- An interesting historical connection: over 2,000 years ago, the ancient Greek mathematician Eratosthenes also studied shadows closely (in a slightly different way) and used this to estimate the circumference of Earth with an error of less than 2%!