Lesson 1
Projecting and Scaling
1.1: Number Talk: Remembering Fraction Division (10 minutes)
Warm-up
This Number Talk gives students an opportunity to recall strategies for computation problems that will arise in the lesson. While many strategies may emerge, the focus of these problems is for students to recall and rehearse a reliable way to divide a mixed number by a whole number. Likely strategies are:
- Use the distributive property to divide each component of the mixed number separately.
- Convert the mixed number into a fraction of the form \(\frac{a}{b}\), then multiply by the reciprocal of the divisor.
Three problems are given. In the limited time available, however, it may not be possible to share every possible strategy. Consider gathering only one or two different strategies per problem.
Launch
Display one problem at a time. Give students 1 minute of quiet think time per problem and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find each quotient. Write your answer as a fraction or a mixed number.
\(6\frac14 \div 2\)
\(10\frac17 \div 5\)
\(8\frac12 \div 11\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see (refer to MLR 2 Collect and Display). Ask students if or how the numbers in the problem impacted their choice of strategy. Point out how the first problem differs from the third in an important way: for the first problem it is not necessary to convert the mixed number to a fraction because the whole number part of the mixed number is evenly divisible by 2.
To involve more students in the conversation, use MLR 7 (Compare and Connect) by asking probing questions and connecting students’ responses, such as:
- “Who can restate _____’s reasoning using your own words?”
- “Does anyone want to add on to _____’s explanation?”
- “Do you agree or disagree _____’s reasoning? Why?”
- “How is _____’s reasoning similar to and different from _____’s reasoning?”
Design Principle(s): Optimize output (for explanation)
1.2: Sorting Rectangles (20 minutes)
Activity
This activity recalls work from grade 7 on scaled copies, purposefully arranging a set of scaled copies to prepare students to understand the process of dilation. If one rectangle is a scaled copy of another, then they can be arranged so that the diagonal of the larger rectangle contains the diagonal of the smaller rectangle. To do this, it is sufficient to line up the rectangles so that the vertices of the right angles at their lower left match up. Students will arrange a set of rectangles into groups with shared diagonals and examine the scale factors relating the rectangles. Afterward, during the discussion, the word dilation is first used, in an informal way, as a way to make scaled copies (of the rectangle in this case). From this point of view, the shared vertex of each set of rectangles is the center of dilation and once we choose an original rectangle from each set, there is a scale factor associated to each copy, namely the scale factor needed to produce the copy from the original.
As an optional additional part to this activity, students may perform a visual test that helps decide whether or not two cut-out figures are scaled copies of one another. The visual test tells whether two cut-out figures are scaled copies of each other by holding each figure at a different distance from the eye and checking if it is possible to make the two figures match up exactly.
Monitor for how students sort the rectangles and how they find measurements of the new rectangles. Encourage them to use what they know about how the rectangles were created rather than measuring each new rectangle (which is likely to introduce errors). Also monitor for how they decide if one rectangle is a scaled copy of another.
Launch
If students will perform the optional eyeball test, tell them that one way to check whether two shapes are scaled copies of each other is to use the “eyeball test.” Students will perform this test for themselves in the activity, but will watch a demonstration first.
- Hold one rectangle up in front of your face in one hand, and another rectangle farther away from your face in the other hand. (The larger rectangle should be farther away than the smaller rectangle.)
- Close one eye.
- If you can adjust your arms so that the rectangles appear to be exactly the same, then they are a match. If it is not possible to adjust your arms so that the rectangles appear to be exactly the same, then they are not a match. Explain to students that their job will be to use the eyeball test to figure out which pairs of their rectangles are matches.
Arrange students in groups of 2. Provide a set of 5 pre-cut rectangles and a long straightedge to each group and, optionally, access to calculators. (Alternatively, you could give each group two whole sheets of paper and instruct them to do the folding and cutting. This option might be attractive if your students would understand the idea of “halving” the measurements better with the concrete experience.)
If students are performing the optional “eyeball test” on pairs of rectangles, instruct them to sort the rectangles into different piles so that all of the rectangles in each pile “match” one another according to the eyeball test. Instruct them to discuss their thinking as a group to reach an agreement.
Supports accessibility for: Conceptual processing
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Rectangles were made by cutting an \(8\frac12\)-inch by 11-inch piece of paper in half, in half again, and so on, as illustrated in the diagram. Find the lengths of each rectangle and enter them in the appropriate table.
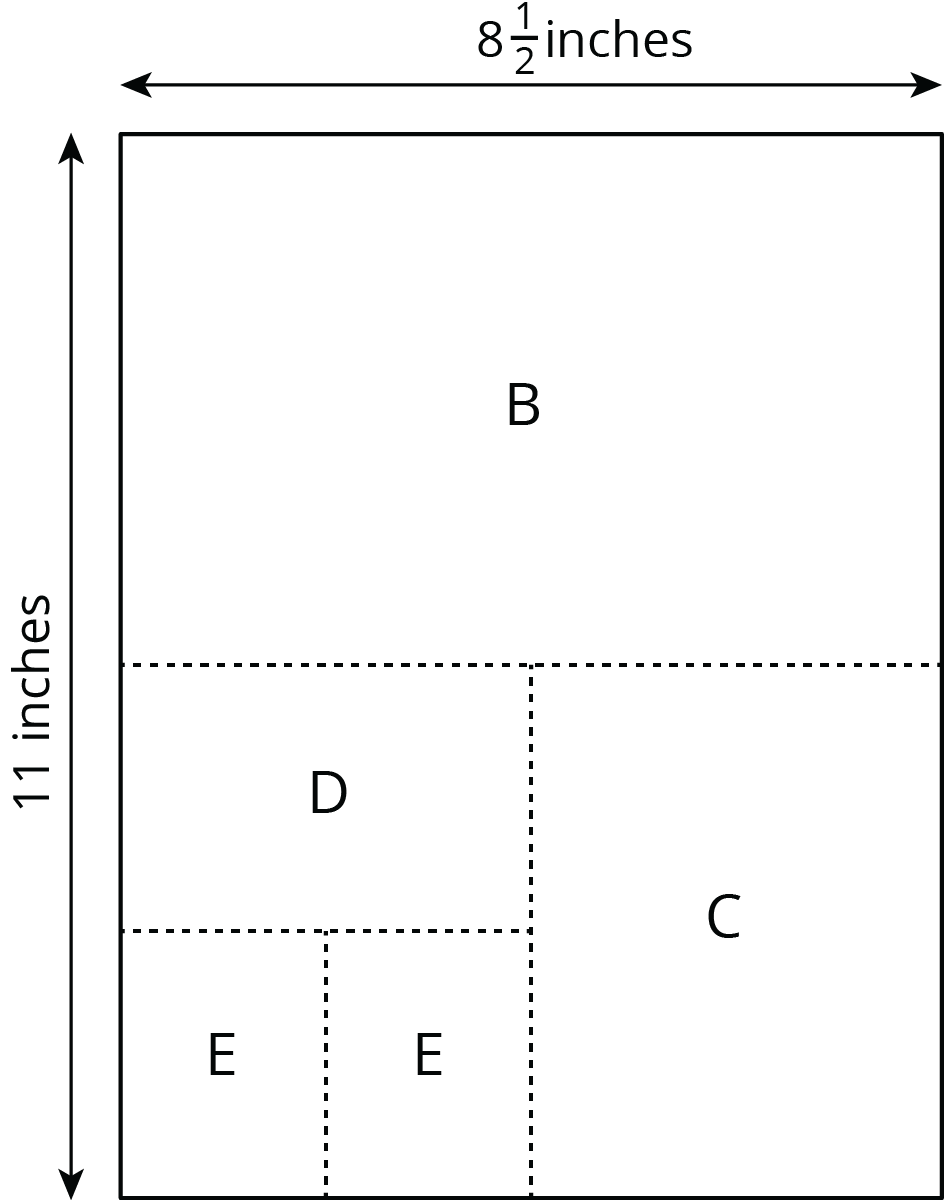
- Some of the rectangles are scaled copies of the full sheet of paper (Rectangle A). Record the measurements of those rectangles in this table.
rectangle length of short side (inches) length of long side (inches) A \(8 \frac{1}{2}\) 11 - Some of the rectangles are not scaled copies of the full sheet of paper. Record the measurements of those rectangles in this table.
rectangle length of short side (inches) length of long side (inches) - Look at the measurements for the rectangles that are scaled copies of the full sheet of paper. What do you notice about the measurements of these rectangles? Look at the measurements for the rectangles that are not scaled copies of the full sheet. What do you notice about these measurements?
- Stack the rectangles that are scaled copies of the full sheet so that they all line up at a corner, as shown in the diagram. Do the same with the other set of rectangles. On each stack, draw a line from the bottom left corner to the top right corner of the biggest rectangle. What do you notice?

- Stack all of the rectangles from largest to smallest so that they all line up at a corner. Compare the lines that you drew. Can you tell, from the drawn lines, which set each rectangle came from?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
In many countries, the standard paper size is not 8.5 inches by 11 inches (called “letter” size), but instead 210 millimeters by 297 millimeters (called “A4” size). Are these two rectangle sizes scaled copies of one another?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students forget how to check if two rectangles are scaled copies of one another, remind them to compare the measurements to see if they have the same scale factor. Students may recall that that scaled copies have corresponding angles of the same measure, but they may not recall that equal angle measurements don’t necessarily mean you have scaled copies.
Activity Synthesis
Ask students how they decided that the \(5\frac{1}{2}\) by \(8\frac{1}{2}\) rectangle is not a scaled copy of the \(8\frac{1}{2}\) by 11 rectangle. Make sure to provide a mathematical explanation since it is not easy to determine visually. For example, there is no single number that you can multiply by \(5\frac{1}{2}\) to get \(8\frac{1}{2}\) and multiply by \(8\frac{1}{2}\) to get 11.
Ask students how they decided that the \(5\frac{1}{2}\) by \(4\frac{1}{4}\) rectangle is a scaled copy of the 11 by \(8\frac{1}{2}\) rectangle, and again, emphasize mathematical explanations based on noticing equivalent ratios.
Emphasize that when all of the rectangles are aligned with the lower left angle matching, by increasing size:
- The diagonals of the rectangles fall into two sets: those that are scaled copies of the full sheet of paper and those that are scaled copies of the half sheet of paper.
- The diagonals of the rectangles that are scaled copies of one another match up.
Tell students that they are going to study a new kind of transformation (to be added to the list from previous work: translations, rotations, and reflections). This new kind of transformation makes scaled copies and is called a dilation. A dilation has a center of dilation(the common vertex for the rectangles in each stack) and a scale factor (4, for example, from Rectangle E to Rectangle A). Different choices of scale factor give scaled copies of different sizes: for example, Rectangle C uses a scale factor of 2, applied to Rectangle E.
1.3: Scaled Rectangles (10 minutes)
Optional activity
This activity continues to examine scaled copies of a rectangle via dividing a rectangle into smaller rectangles. In this activity, the focus is more on the scale factor and the language of scaled copies, emphasizing the link with work students did in grade 7. Unlike in the previous task, there are no given dimensions for any of the rectangles. Students need to find the scale factor using their understanding of the meaning of scale factor and the fact that the rectangles are divided evenly.
Monitor how students reason about the scale factor. They could use the diagram to see how many times as long and wide one rectangle is compared to another. They could also use what they know about how the area of rectangles changes in scaled copies. Select students who use these approaches to share during the discussion.
Launch
Tell students that they are going to examine a different set of rectangles and determine scale factors for pairs which are scaled copies of one another. Briefly, ask students to interpret what is meant by “evenly divided.” (Rectangle R is cut exactly in half vertically and horizontally, and also one of its quadrants is cut exactly in thirds vertically and horizontally.) Students may want to use a ruler to validate their understanding of what “evenly divided” means.
Give students 5 minutes quiet work time followed by a whole-class discussion.
Supports accessibility for: Language; Social-emotional skills
Design Principle(s): Maximize meta-awareness
Student Facing
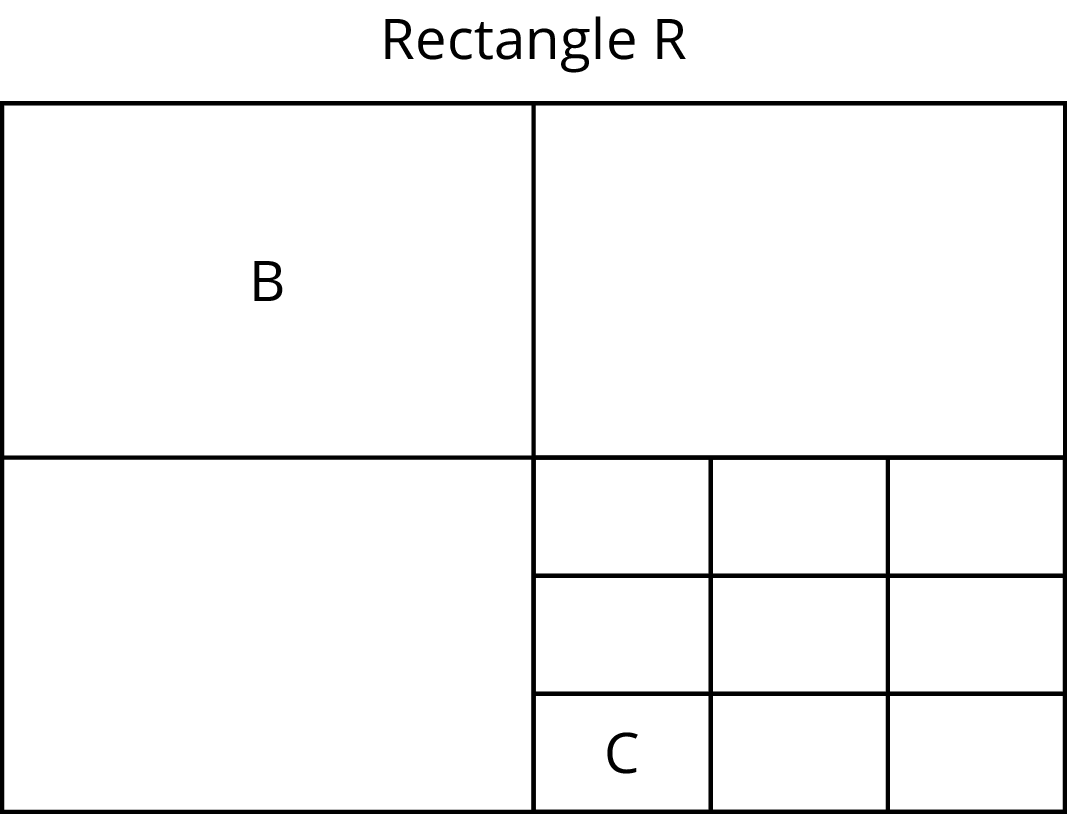
Here is a picture of Rectangle R, which has been evenly divided into smaller rectangles. Two of the smaller rectangles are labeled B and C.
- Is \(B\) a scaled copy of \(R\)? If so, what is the scale factor?
- Is \(C\) a scaled copy of \(B\)? If so, what is the scale factor?
- Is \(C\) a scaled copy of \(R\)? If so, what is the scale factor?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask selected students to share their solutions. Then ask these questions:
- “Why is rectangle B a scaled copy of rectangle R?” (The length and width in both cases have been multiplied by the same number because the rectangles are divided evenly.)
- “How are the scale factors from R to B and B to C related to the scale factor from R to C?” (The latter is the product of the former.)
- “Does the diagonal from top left to lower right of Rectangle R go through opposite vertices of one rectangle of each size?” (Yes.)
Lesson Synthesis
Lesson Synthesis
In previous lessons, we have studied rigid transformations, specifically translations, rotations, and reflections. When we apply a sequence of rigid transformations to a figure, we change the figure’s location and orientation in the plane but not its size. In this lesson, we began to study a new “move,” which makes scaled copies of figures (and hence can change their size!) This new move is called a dilation. We will introduce a formal definition of dilation in the next lesson and then we will investigate how figures change when dilations are allowed in addition to rigid transformations.
1.4: Cool-down - What is a Dilation? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Scaled copies of rectangles have an interesting property. Can you see what it is?
Here, the larger rectangle is a scaled copy of the smaller one (with a scale factor of \(\frac{3}{2}\)). Notice how the diagonal of the large rectangle contains the diagonal of the smaller rectangle. This is the case for any two scaled copies of a rectangle if we line them up as shown. If two rectangles are not scaled copies of one another, then the diagonals do not match up. In this unit, we will investigate how to make scaled copies of a figure.
