Lesson 6
Similarity
6.1: Equivalent Expressions (5 minutes)
Warm-up
This warm-up prompts students to use what they know about operations and properties of operations to create related expressions. While many warm-ups encourage students to work mentally and verbally, students will write their responses to this prompt. Since many different responses are possible, the task is accessible to all students and provides an opportunity to hear how each student reasons about the operations. Some different ideas that may emerge are:
- commutative property
- distributive property
- inverse operations
- adjusting factors (for example, doubling and halving)
Examples of each are given in the student response section. Students are not expected to use these terms, but highlight the terms if students do use them.
Launch
Arrange students in groups of 2. Tell students they are writing a list of several expressions equivalent to \(10 (2 + 3) - 8 \boldcdot 3\). Give students 2 minutes of quiet think time followed by 1 minute to discuss their responses with a partner.
Student Facing
Use what you know about operations and their properties to write three expressions equivalent to the expression shown.
\(\displaystyle 10 (2 + 3) - 8 \boldcdot 3\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Much of the discussion takes place between partners. Ask students to share any expressions that they aren't sure about, but try to resolve these and move on quickly.
6.2: Similarity Transformations (Part 1) (20 minutes)
Activity
In this activity, students learn that two figures are similar when there is a sequence of translations, reflections, rotations and dilations that takes one figure to the other. Students practice discovering these sequences for two pairs of figures.
When two shapes are similar but not congruent, the sequence of steps showing the similarity usually has a single dilation and then the rest of the steps are rigid transformations. The dilation can come at any time. It does not matter which figure you start with. An important thing for students to notice in this activity is that there is more than one sequence of transformations that show two figures are similar. Monitor for students who insert a dilation at different places in the sequence. Also monitor for how students find the scale factor for the hexagons.
Launch
Before beginning this task, define what it means for two figures to be similar.
Tell students: We have talked about how one figure can be a scaled copy of another. This relationship goes in both directions. For example, if triangle \(DEF\) is a scaled copy of triangle \(ABC\) with scale factor of 2 then triangle \(ABC\) is a scaled copy of triangle \(DEF\) with scale factor \(\frac12\). We have learned that the transformation that creates scaled copies is called a dilation.
We say that triangles \(ABC\) and \(DEF\) are similar. The previous unit explored how translations, rotations, and reflections define congruent figures. The inclusion of dilations can change the size of the figure as well as its location and orientation.
We will start our investigation of similar figures by identifying sequences of translations, rotations, reflections, and dilations that show two figures are similar. Demonstrate using this example.
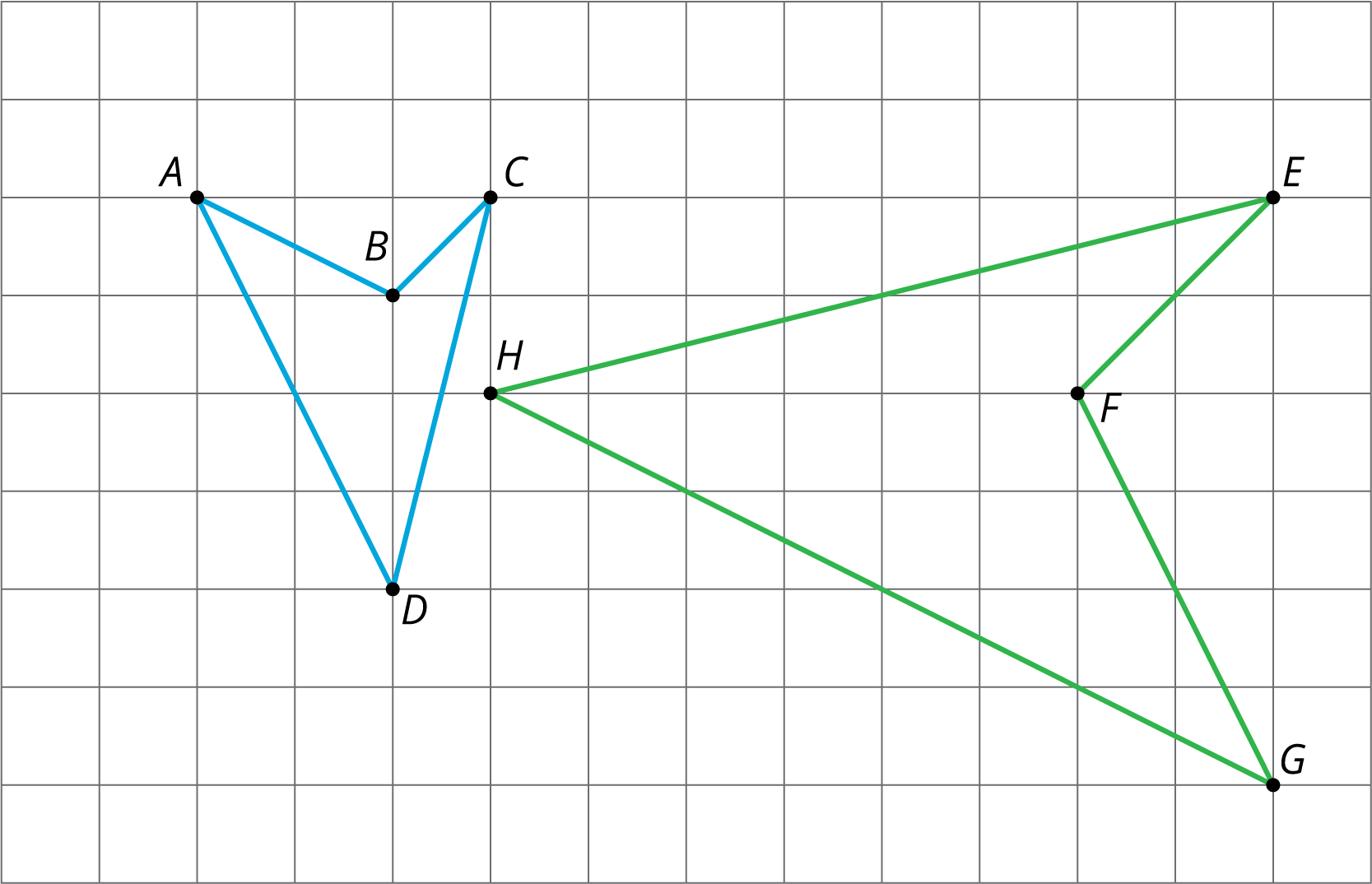
There are many methods to make this work. Explain at least two. First, identify the corresponding parts. Then come up with a plan to take one figure to the other. Ensure students understand, through demonstration with this example, that the work of showing two figures are similar requires communicating the details of each transformation in the sequence with enough precision. Some sample methods:
- Method 1 (\(ABCD\) to \(GFEH\): Dilate, Translate, Rotate, Reflect)
- Dilate using \(D\) as the center with scale factor 2.
- Translate \(D\) to \(H\)
- Rotate using \(H\) as the center clockwise by 90 degrees
- Reflect using the line that contains \(H\) and \(F\).
- Method 2 (\(ABCD\) to \(GFEH\): Reflect, Translate, Rotate, Dilate)
- Reflect using the line that contains \(D\) and \(B\).
- Translate \(D\) to \(H\).
- Rotate using \(H\) as the center clockwise by 90 degrees
- Dilate using \(H\) as the center with a scale factor of 2.
- Method 3 (\(ABCD\) to \(GFEH\): Translate, Rotate, Reflect, Dilate)
- Translate \(B\) to \(F\).
- Rotate using \(F\) as the center clockwise by 90 degrees.
- Reflect using the line that contains \(F\) and \(H\).
- Dilate using \(F\) as the center with scale factor 2.
These arguments can also be applied to figures that are not on a grid: the grid helps to identify directions and distances of translation, 90 degree angles of rotation, and horizontal and vertical lines of reflection.
If using the print version, provide access to geometry toolkits. If using the digital version, remind students of the meaning and functionality of each transformation tool, as necessary.
Supports accessibility for: Memory; Language
Student Facing
-
Triangle \(EGH\) and triangle \(LME\) are similar. Find a sequence of translations, rotations, reflections, and dilations that shows this.
-
Hexagon \(ABCDEF\) and hexagon \(HGLKJI\) are similar. Find a sequence of translations, rotations, reflections, and dilations that shows this.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Before beginning this task, define what it means for two figures to be similar.
Tell students: We have talked about how one figure can be a scaled copy of another. This relationship goes in both directions. For example, if triangle \(DEF\) is a scaled copy of triangle \(ABC\) with scale factor of 2 then triangle \(ABC\) is a scaled copy of triangle \(DEF\) with scale factor \(\frac12\). We have learned that the transformation that creates scaled copies is called a dilation.
We say that triangles \(ABC\) and \(DEF\) are similar. The previous unit explored how translations, rotations, and reflections define congruent figures. The inclusion of dilations can change the size of the figure as well as its location and orientation.
We will start our investigation of similar figures by identifying sequences of translations, rotations, reflections, and dilations that show two figures are similar. Demonstrate using this example.

There are many methods to make this work. Explain at least two. First, identify the corresponding parts. Then come up with a plan to take one figure to the other. Ensure students understand, through demonstration with this example, that the work of showing two figures are similar requires communicating the details of each transformation in the sequence with enough precision. Some sample methods:
- Method 1 (\(ABCD\) to \(GFEH\): Dilate, Translate, Rotate, Reflect)
- Dilate using \(D\) as the center with scale factor 2.
- Translate \(D\) to \(H\)
- Rotate using \(H\) as the center clockwise by 90 degrees
- Reflect using the line that contains \(H\) and \(F\).
- Method 2 (\(ABCD\) to \(GFEH\): Reflect, Translate, Rotate, Dilate)
- Reflect using the line that contains \(D\) and \(B\).
- Translate \(D\) to \(H\).
- Rotate using \(H\) as the center clockwise by 90 degrees
- Dilate using \(H\) as the center with a scale factor of 2.
- Method 3 (\(ABCD\) to \(GFEH\): Translate, Rotate, Reflect, Dilate)
- Translate \(B\) to \(F\).
- Rotate using \(F\) as the center clockwise by 90 degrees.
- Reflect using the line that contains \(F\) and \(H\).
- Dilate using \(F\) as the center with scale factor 2.
These arguments can also be applied to figures that are not on a grid: the grid helps to identify directions and distances of translation, 90 degree angles of rotation, and horizontal and vertical lines of reflection.
If using the print version, provide access to geometry toolkits. If using the digital version, remind students of the meaning and functionality of each transformation tool, as necessary.
Supports accessibility for: Memory; Language
Student Facing
-
Triangle \(EGH\) and triangle \(LME\) are similar. Find a sequence of translations, rotations, reflections, and dilations that shows this.

-
Hexagon \(ABCDEF\) and hexagon \(HGLKJI\) are similar. Find a sequence of translations, rotations, reflections, and dilations that shows this.

Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The same sequence of transformations takes Triangle A to Triangle B, takes Triangle B to Triangle C, and so on. Describe a sequence of transformations with this property.
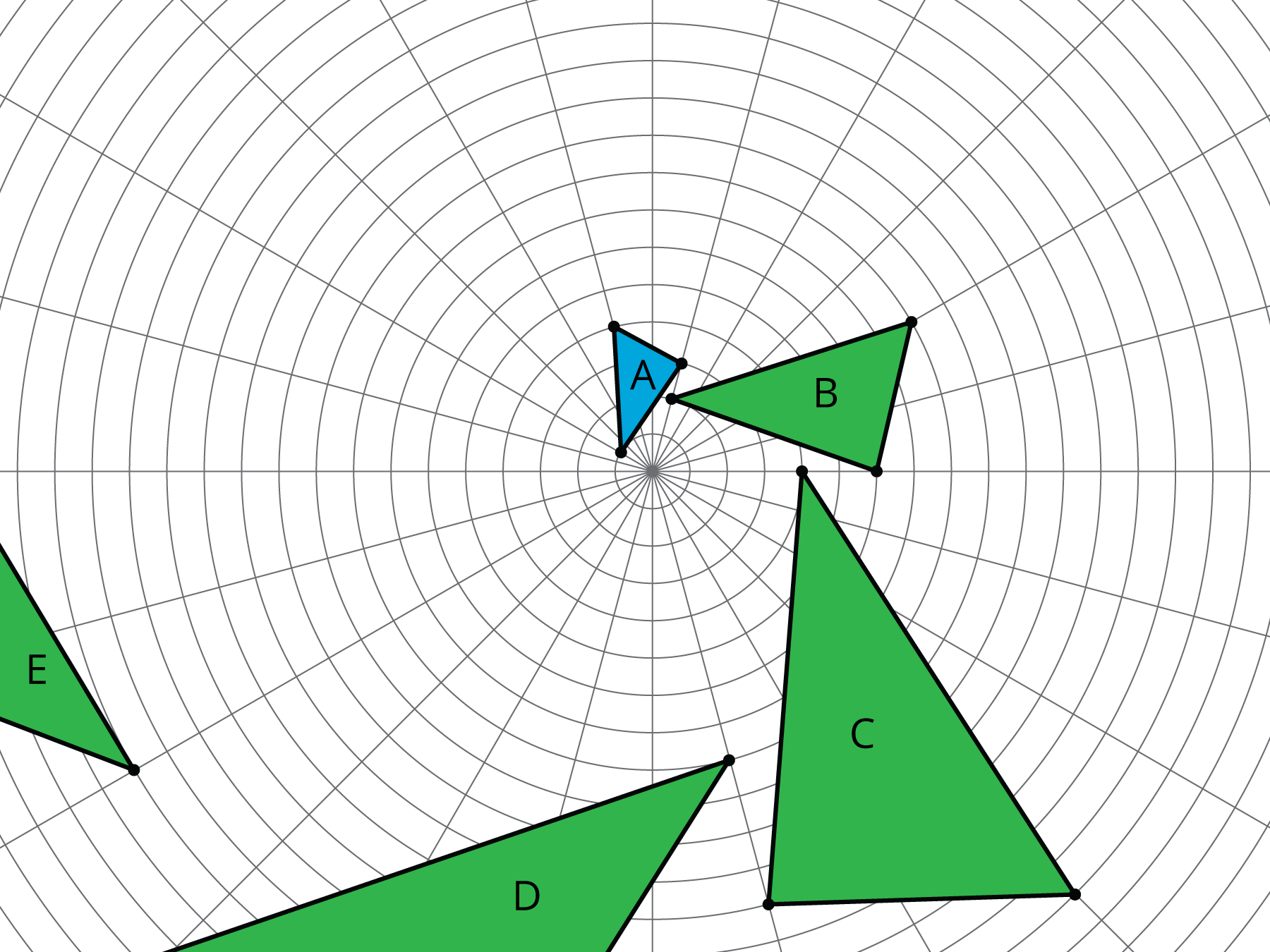
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students do not recall the three types of rigid transformations, refer them to the classroom display that provides an example of a rotation, a reflection, and a translation.
For the second problem, students may need encouragement to experiment moving the shapes (using tracing paper for example). If they get stuck finding the scale factor, tell them that they can approximate by measuring sides of the two figures.
Activity Synthesis
Select students to give a variety of solutions for the different problems. Point out that there are multiple ways to do each pair and any valid sequence is allowed. Ensure that students communicate each transformation in the sequence in sufficient detail.
Design Principles(s): Optimize output (for explanation); Maximize meta-awareness
6.3: Similarity Transformations (Part 2) (10 minutes)
Activity
This activity helps students visualize what happens to figures under different kinds of transformations. Students practice identifying which transformations might be used in the sequence of translations, rotations, reflections, and dilations in order to show figures are similar. By recognizing patterns in the image results after using certain transformations (MP8), students may be able to apply this to finding transformations for other problems. Students should pay special attention to see the connection between the orientations of the original figure and the resulting images after transformation.
Encourage students to draw rough sketches though it is also ok to use patty paper, for example, to execute the rigid motions. For the dilations, however, it could become time consuming to choose an explicit scale factor and measure carefully. Make sure, after students have worked on the first problem, to show some examples of sketches that are not exact but capture the main features of the figure.
Launch
The figure in this task is intended to resemble a hand with all of the fingers together and the thumb sticking out. Encourage students to “sketch” the resulting images for this task (or make tracing paper available, indicating that the images do not need to be exact). They do not need to make the side lengths, angles, etc. perfect, but it should be clear where the corresponding parts of the image are and whether it is larger or smaller than the original. Other activities in this unit will ask students to be precise in their use of transformations, but the goal of this activity is to get an idea of how the different transformations affect a figure’s image.
Select a few good examples of student work (including some that have been sketched free hand) to share with the class after problem 1, in order to clearly communicate the expectation for level of precision.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Student Facing
Sketch figures similar to Figure A that use only the transformations listed to show similarity.

- A translation and a reflection. Label your sketch Figure B.
Pause here so your teacher can review your work. - A reflection and a dilation with scale factor greater than 1. Label your sketch Figure C.
- A rotation and a reflection. Label your sketch Figure D.
- A dilation with scale factor less than 1 and a translation. Label your sketch Figure E.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students choose an exact scale factor, or measure the exact angle sizes, explain that precise measurements are not needed in this task. At this point, they are just sketching similar figures.
Activity Synthesis
Select students to display their answers for each of the questions. Ask students to notice things the answers have in common so that they can make connections to the types of transformations that might be useful in showing that two figures are similar.
Assuming that the rotations are not through an angle that is a multiple of \(360^\circ\) and that the translations have a non-zero horizontal or vertical part, point out that:
- Dilations will create larger or smaller copies depending on the scale factor as seen in previous lessons.
- Translations will slide the figure in some direction.
- Rotations will “tilt” or “turn” the figure.
- Reflections will change the handedness so that the resulting image will look like the back of a right hand instead of the back of a left hand as in the original image.
6.4: Methods for Translations and Dilations (10 minutes)
Optional activity
The purpose of this task is for students to practice showing that two shapes are similar using only a few pre-determined rigid motions and dilations. Some students will start with triangle \(ABC\) and take this to triangle \(DEF\) while other start with \(DEF\) and take this to \(ABC\). While there is flexibility in either direction, one way of getting from \(DEF\) to \(ABC\) is to “undo” the moves that take \(ABC\) to \(DEF\).
Monitor for students who use different centers of dilation in their sequence, particularly as the first step in the sequence. Invite these students to share, highlighting the fact that two dilations with the same scale factor but different centers differ by a translation. Also monitor for students whose sequences of rigid motions and dilations are the same but in the opposite order, one set taking \(ABC\) to \(DEF\) and the opposite taking \(DEF\) back to \(ABC\). Select these students to share this important observation during the discussion.
Launch
Again, remind students that two figures are similar if there is a sequence of translations, rotations, reflections, and dilations that takes one figure to another. Tell them that they need to find at least one way to show that triangle \(ABC\) and triangle \(DEF\) are similar using only the transformations they are given on their cards.
Arrange students in groups of 2. Give each group one complete set of cards.
Supports accessibility for: Language; Social-emotional skills
Student Facing
Your teacher will give you a set of five cards and your partner a different set of five cards. Using only the cards you were given, find at least one way to show that triangle \(ABC\) and triangle \(DEF\) are similar. Compare your method with your partner’s method. What is the same about your methods? What is different?

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might think that is it necessary to perform transformations in the same order or that one particular point needs to be the center. If partners choose the same methods, prompt them to try it another way that will have the same end result.
Activity Synthesis
Invite selected students to share, highlighting methods of moving \(ABC\) to \(DEF\) and \(DEF\) to \(ABC\) which are “opposite” of one another, for example dilations with center \(P\) and reciprocal scale factors.
As students share their responses, highlight these points:
- The scale factors for the dilations are reciprocals regardless of when the dilations are done in the sequence.
- If used, the translations are inverses of each other (eg “Translate \(A\) to \(D\)” instead of “Translate \(D\) to \(A\)”).
- Dilations with different centers but the same scale factor produce congruent figures that differ by a translation.
- The order in which transformations are applied can influence the result.
One important conclusion (the third bullet point) is that when you are showing that two figures are similar, you can pick any point as the center of dilation if you know the scale factor, because you can always adjust the position using a translation.
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Review the definition of similar figures and any important insights that arose during the lesson. Insights to highlight:
Two figures are similar if there is a sequence of translations, rotations, reflections, and dilations that maps one to the other. Scaled copies of figures, studied in grade 7, are all examples of similar figures. In this lesson, we found transformations that showed that two figures were similar.
We saw that there is more than one sequence of transformations that shows two figures are similar. One way to think about it is that you need to use a dilation to make corresponding side lengths the same size. The figures will be congruent after this step. Once you do that, you just need to find a sequence of rigid transformations that align the congruent figures. You can also do it the other way, by bringing the figures into alignment and then dilating one to match up with the other.
Add the term similar along with a definition and example to your classroom display such as a word wall or anchor chart.
6.5: Cool-down - Showing Similarity (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Let’s show that triangle \(ABC\) is similar to triangle \(DEF\):
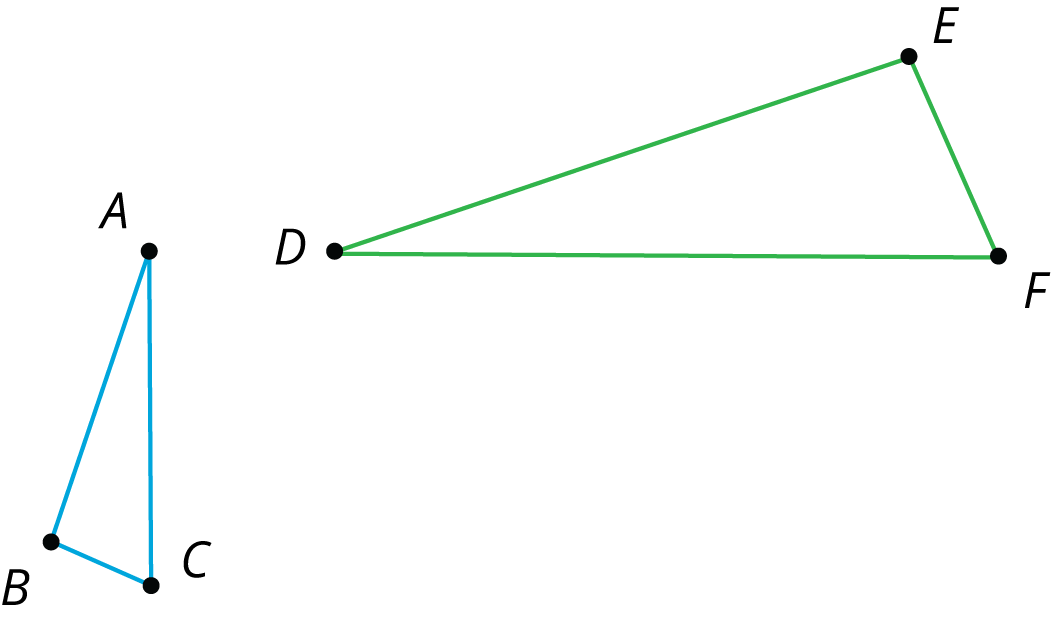
Two figures are similar if one figure can be transformed into the other by a sequence of translations, rotations, reflections, and dilations. There are many correct sequences of transformations, but we only need to describe one to show that two figures are similar.
One way to get from \(ABC\) to \(DEF\) follows these steps:
- step 1: reflect across line \(f\)
- step 2: rotate \(90^\circ\) counterclockwise around \(D\)
- step 3: dilate with center \(D\) and scale factor 2
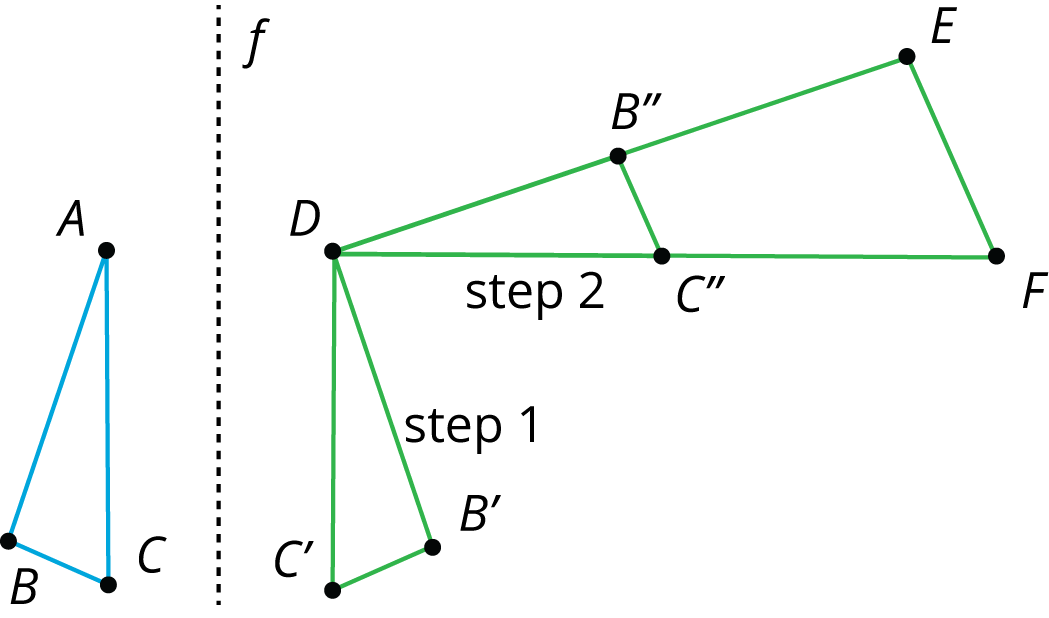
Another way would be to dilate triangle \(ABC\) by a scale factor of 2 with center of dilation \(A\), then translate \(A\) to \(D\), then reflect over a vertical line through \(D\), and finally rotate it so it matches up with triangle \(DEF\). What steps would you choose to show the two triangles are similar?