Lesson 12

Using Equations for Lines

View Student Lesson

Problem 1

Select all the points that are on the line through \((0,5)\) and \((2,8)\).

A:

\((4,11)\)

B:

\((5,10)\)

C:

\((6,14)\)

D:

\((30,50)\)

E:

\((40,60)\)

Solution

For access, consult one of our IM Certified Partners.

Problem 2

All three points displayed are on the line. Find an equation relating \(x\) and \(y\).

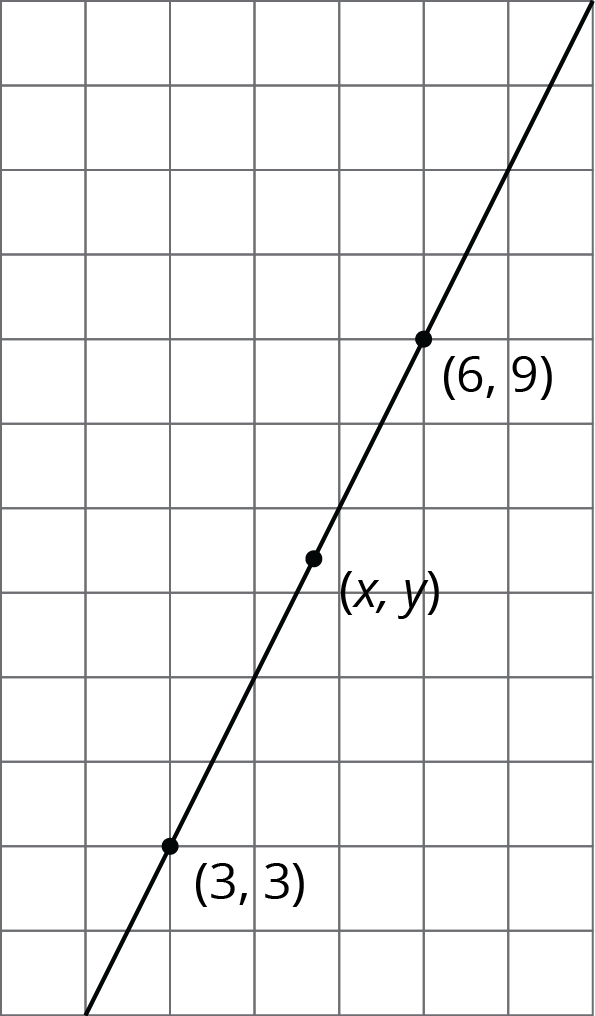
Coordinate plane, first quadrant. Line is drawn through 3 comma 3, x comma y, and 6 comma 9

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Here is triangle \(ABC\).

Triangle on graph. A at 2 comma 0, B at 5 comma 0, C at 5 comma 1.
  1. Draw the dilation of triangle \(ABC\) with center \((2,0)\) and scale factor 2.
  2. Draw the dilation of triangle \(ABC\) with center \((2,0)\) and scale factor 3.
  3. Draw the dilation of triangle \(ABC\) with center \((2,0)\) and scale factor \(\frac 1 2\).
  4. What are the coordinates of the image of point \(C\) when triangle \(ABC\) is dilated with center \((2,0)\) and scale factor \(s\)?
  5. Write an equation for the line containing all possible images of point \(C\).

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Here are some line segments.

Point A, segment B C and 3 other segments, E D, G J and F H.
  1. Which segment is a dilation of \(\overline{BC}\) using \(A\) as the center of dilation and a scale factor of \(\frac23\)?
  2. Which segment is a dilation of \(\overline{BC}\) using \(A\) as the center of dilation and a scale factor of \(\frac32\)?
  3. Which segment is not a dilation of \(\overline{BC}\), and how do you know?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 4.)