Lesson 11
Writing Equations for Lines
Lesson Narrative
The previous lesson introduces the idea of slope for a line. In this lesson, the slope is used to write a relationship satisfied by any point on a line. The key idea is to introduce a general or variable point on a line, that is a point with coordinates \((x,y)\). These variables \(x\) and \(y\) can take any values as long as those values represent a point on the line. Because all slope triangles lead to the same value of slope, this general point can be used to write a relationship satisfied by all points on the line.
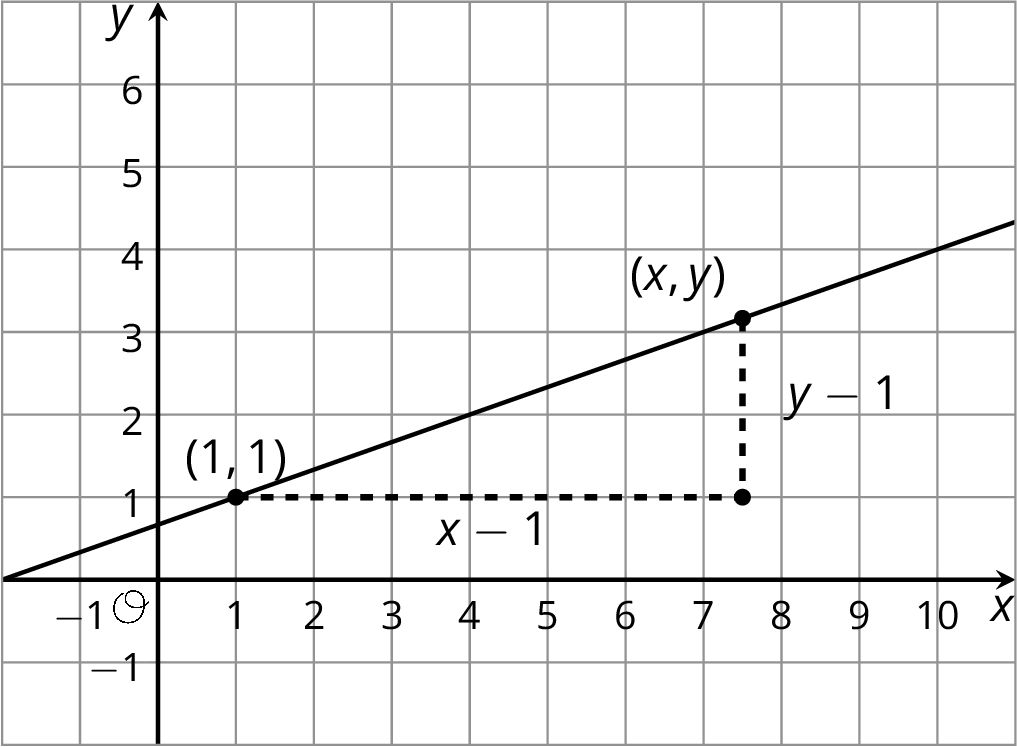
In this example, the slope of the line is \(\frac{1}{3}\) since the points \((1,1)\) and \((4,2)\) are on the line. The slope triangle in the picture has vertical length \(y-1\) and horizontal length \(x-1\) so this gives the equation \(\displaystyle \frac{y-1}{x-1} = \frac{1}{3}\) satisfied by any point on the line (other than \((1,1)\)). This concise way of expressing which points lie on a line will be developed further in future units.
Learning Goals
Teacher Facing
- Create an equation relating the quotient of the vertical and horizontal side lengths of a slope triangle to the slope of a line.
- Justify (orally) whether a point is on a line by finding quotients of horizontal and vertical distances.
Student Facing
Let’s explore the relationship between points on a line and the slope of the line.
Learning Targets
Student Facing
- I can decide whether a point is on a line by finding quotients of horizontal and vertical distances.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |