Lesson 15
Adding the Angles in a Triangle
Lesson Narrative
In this lesson, the focus is on the interior angles of a triangle. What can we say about the three interior angles of a triangle? Do they have special properties?
The lesson opens with an optional activity looking at different types of triangles with a particular focus on the angle combinations of specific acute, right, and obtuse triangles. After being given a triangle, students form groups of 3 by identifying two other students with a triangle congruent to their own. After collecting some class data on all the triangles and their angles, they find that the sum of the angle measures in all the triangles turns out to be 180 degrees.
In the next activity, students observe that if a straight angle is decomposed into three angles, it appears that the three angles can be used to create a triangle. Together the activities provide evidence of a close connection between three positive numbers adding up to 180 and having a triangle with those three numbers as angle measures.
A new argument is needed to justify this relationship between three angles making a line and three angles being the angles of a triangle. This is the topic of the following lesson.
Learning Goals
Teacher Facing
- Comprehend that a straight angle can be decomposed into 3 angles to construct a triangle.
- Justify (orally and in writing) that the sum of angles in a triangle is 180 degrees using properties of rigid motions.
Student Facing
Let’s explore angles in triangles.
Required Materials
Required Preparation
Print copies of the Tear it Up blackline master. Prepare 1 copy for every group of 4 students. From the geometry toolkit, students will need scissors.
If you are doing the optional Find All Three activity, prepare 1 copy of the Find All Three blackline master for every 15 students. Cut these up ahead of time.
Learning Targets
Student Facing
- If I know two of the angle measures in a triangle, I can find the third angle measure.
Glossary Entries
-
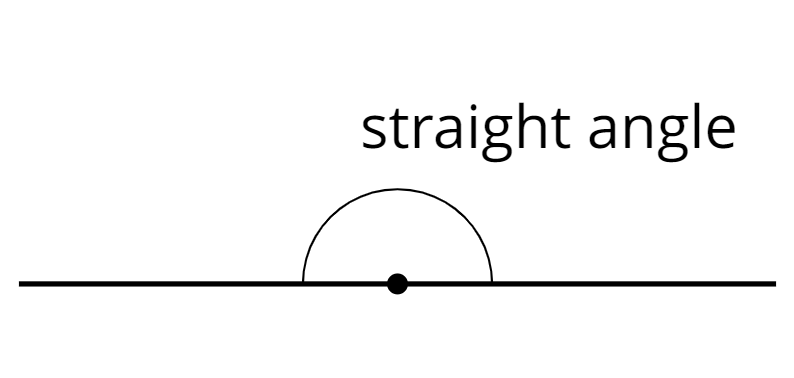
straight angle
A straight angle is an angle that forms a straight line. It measures 180 degrees.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |