Lesson 6
Describing Transformations
6.1: Finding a Center of Rotation (5 minutes)
Warm-up
Sometimes it is easy to forget to communicate all of the vital information about a transformation. In this case, the center of a rotation is left unspecified. Students do not need to develop a general method for finding the center of rotation, given a polygon and its rotated image. They identify the center in one situation and this can be done via geometric intuition and a little trial and error.
Launch
Arrange students in groups of 2 and provide access to geometry toolkits. Tell students that they have a diagram of a figure and its rotated image and that they need to identify the center of rotation. Give them 2 minutes of quiet work time and an opportunity to share with a partner, followed by a whole-class discussion.
Student Facing
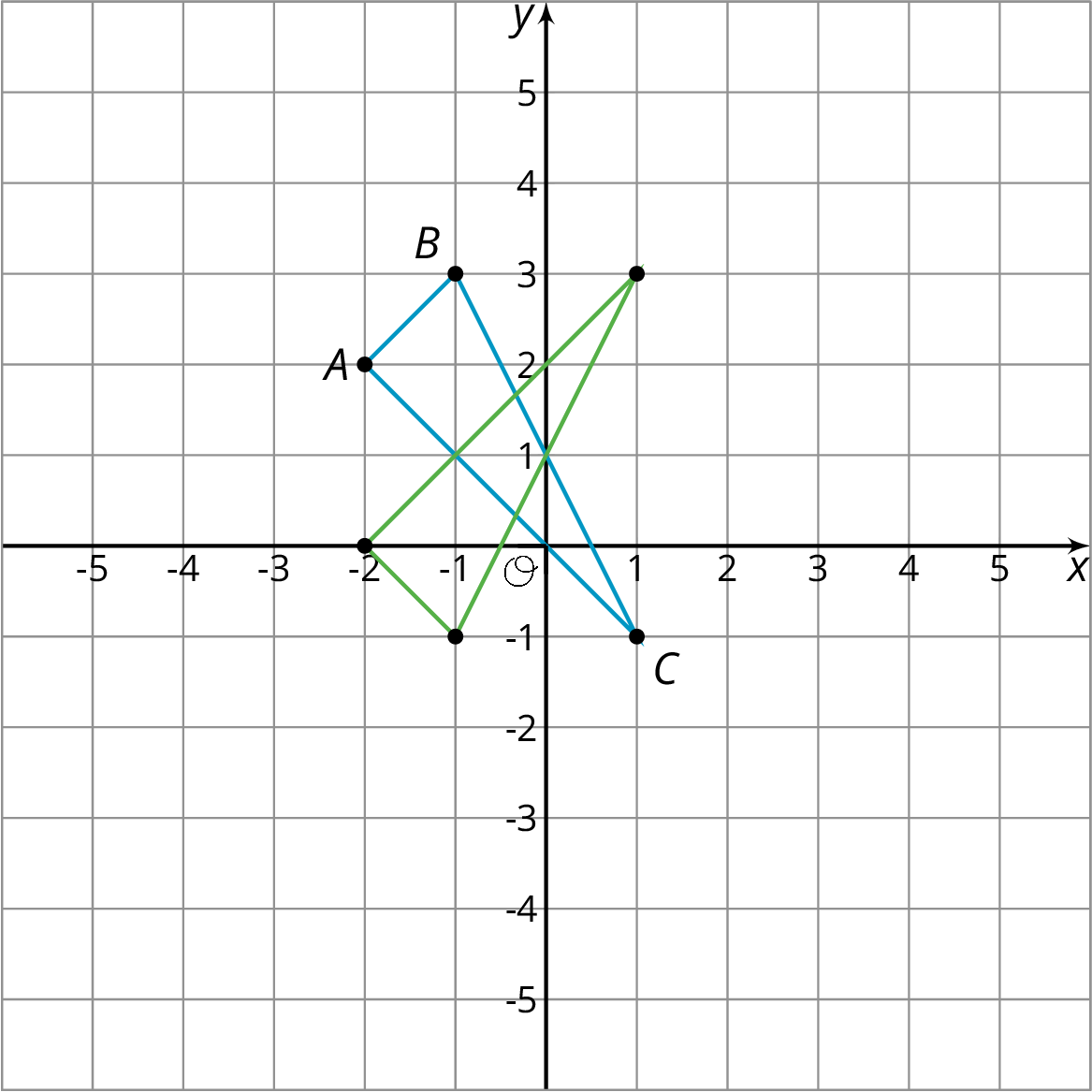
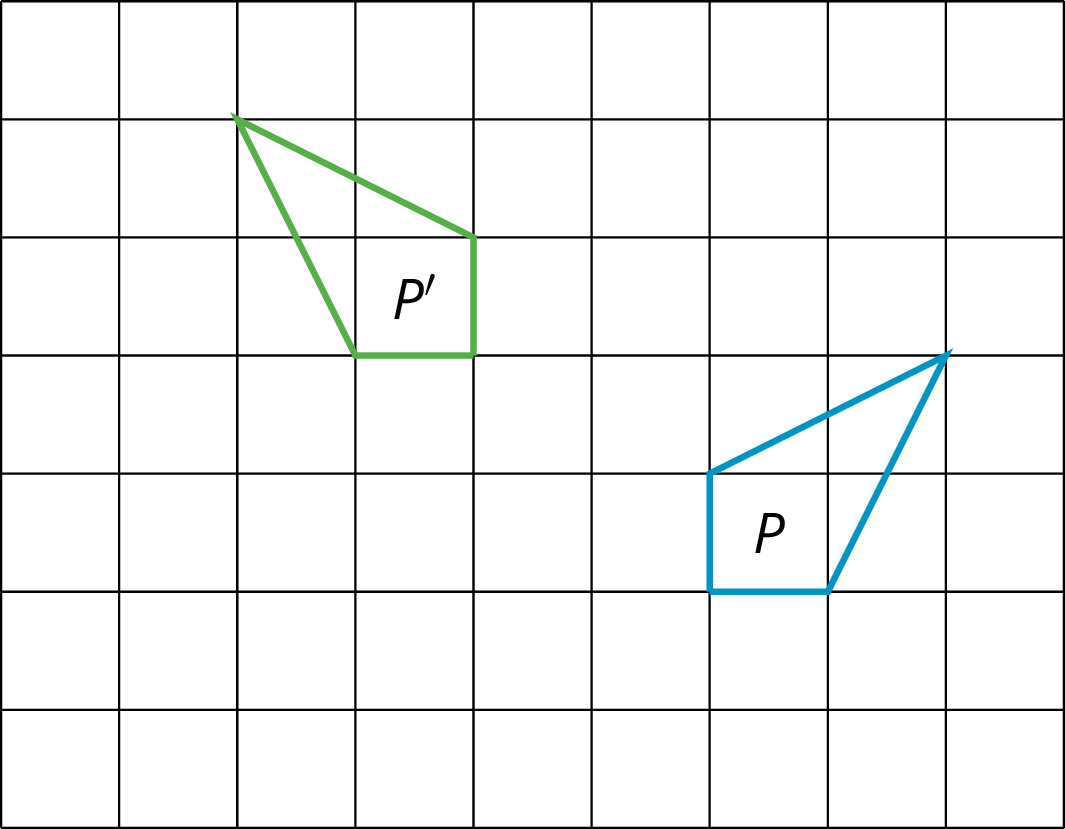
Andre performs a 90-degree counterclockwise rotation of Polygon P and gets Polygon P’, but he does not say what the center of the rotation is. Can you find the center?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may have trouble getting started. Suggest that they trace P on to tracing paper and try rotating it \(90^\circ\). How must they rotate it to get it to land on P'? Where is the center of the "spin"?
Activity Synthesis
Emphasize that it is important to communicate clearly. When we perform a transformation, we should provide the information necessary for others to understand what we have done. For a rotation, this means communicating:
- The center of the rotation.
- The direction of the rotation (clockwise or counterclockwise).
- The angle of rotation.
The grid provides extra structure that helps to identify these three parts of the rotation. Invite students to share how they identified the center of rotation. Methods may include:
- Experimenting with tracing paper.
- Understanding that the rotation does not change the distance between the center of rotation and each vertex, so the center should be the same distance from each vertex and its image.
6.2: Info Gap: Transformation Information (30 minutes)
Activity
This info gap activity gives students an opportunity to determine and request the information needed to perform a transformation in the coordinate plane. A sample pair of cards looks as follows:
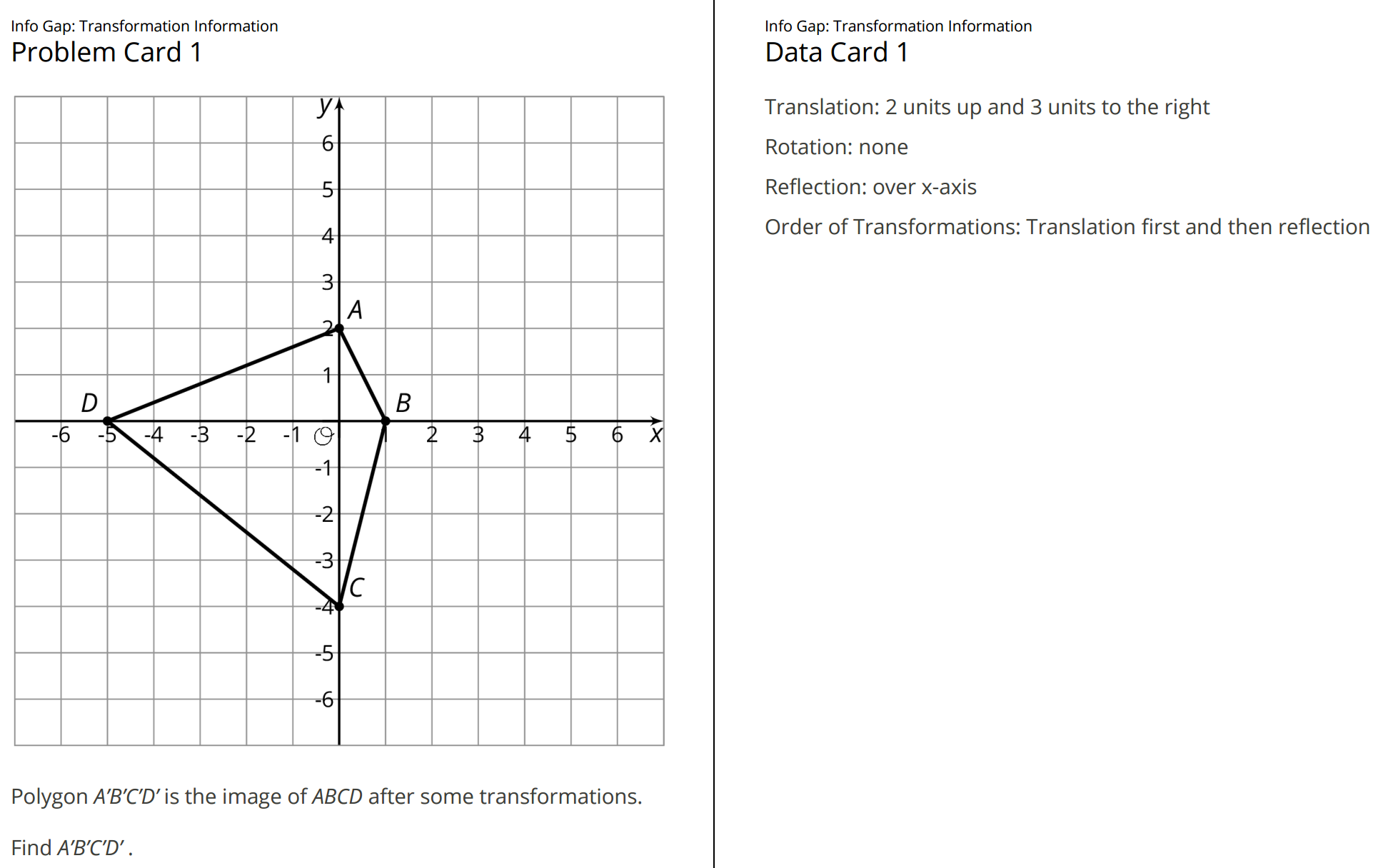
Students likely need several rounds to determine the information they need.
- They need to know which transformations were applied (i.e., translation, rotation, or reflection)
- They need to determine the order in which the transformations were applied.
- They need to remember what information is needed to describe a translation, rotation, or reflection.
Monitor for students who successfully determine or remember each of these three important pieces of information as well as students who have partially but not completely solved the problem. Students may not realize that the order in which the transformations are applied is important, and this should be addressed in the Synthesis.
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
Launch
Tell students they will continue to describe transformations using coordinates. Explain the info gap structure, and consider demonstrating the protocol if students are unfamiliar with it.
Arrange students in groups of 2. Provide access to graph paper. In each group, distribute a problem card to one student and a data card to the other student. After you review their work on the first problem, give them the cards for a second problem and instruct them to switch roles.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate Conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Sometimes two transformations, one performed after the other, have a nice description as a single transformation. For example, instead of translating 2 units up followed by translating 3 units up, we could simply translate 5 units up. Instead of rotating 20 degrees counterclockwise around the origin followed by rotating 80 degrees clockwise around the origin, we could simply rotate 60 degrees clockwise around the origin.
Can you find a simple description of reflecting across the \(x\)-axis followed by reflecting across the \(y\)-axis?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle to ask their partner for all of the information they need or may ask a question that is not sufficiently precise, such as, “What are the transformations?” Ask these students what kinds of transformations they have worked with. What information is needed to perform a translation? What about a rotation or reflection? Encourage them to find out which transformations they need to perform (Is there a translation? Is there a rotation?) and then find out the information they need for each transformation.
Activity Synthesis
After students have completed their work, share the correct answers and ask students to discuss the process of solving the problems. Some guiding questions:
- "How did using coordinates help in talking about the problem?"
- "Was the order in which the transformations were applied important? Why?"
- "If this same problem were a picture on a grid without coordinates, how would you talk about the points?"
Highlight for students that one advantage of the coordinate plane is that it allows us to communicate information about transformations precisely. Here is what is needed for each type of transformation (consider showing one example of each while going through the different transformations):
- For a translation, the distance of vertical and horizontal components
- For a rotation, the center of rotation, the direction of rotation, and the angle of rotation
- For a reflection, the line of reflection
Lesson Synthesis
Lesson Synthesis
Ask students to choose which of the three transformations they have studied so far (translation, reflection, rotation) is their favorite and give 2–3 minutes for students to write a few sentences explaining why. Have students first share their explanations with a partner and then invite students to share their favorite with the class.
6.3: Cool-down - Describing a Sequence of Transformations (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The center of a rotation for a figure doesn’t have to be one of the points on the figure. To find a center of rotation, look for a point that is the same distance from two corresponding points. You will probably have to do this for a couple of different pairs of corresponding points to nail it down.
When we perform a sequence of transformations, the order of the transformations can be important. Here is triangle \(ABC\) translated up two units and then reflected over the \(x\)-axis.
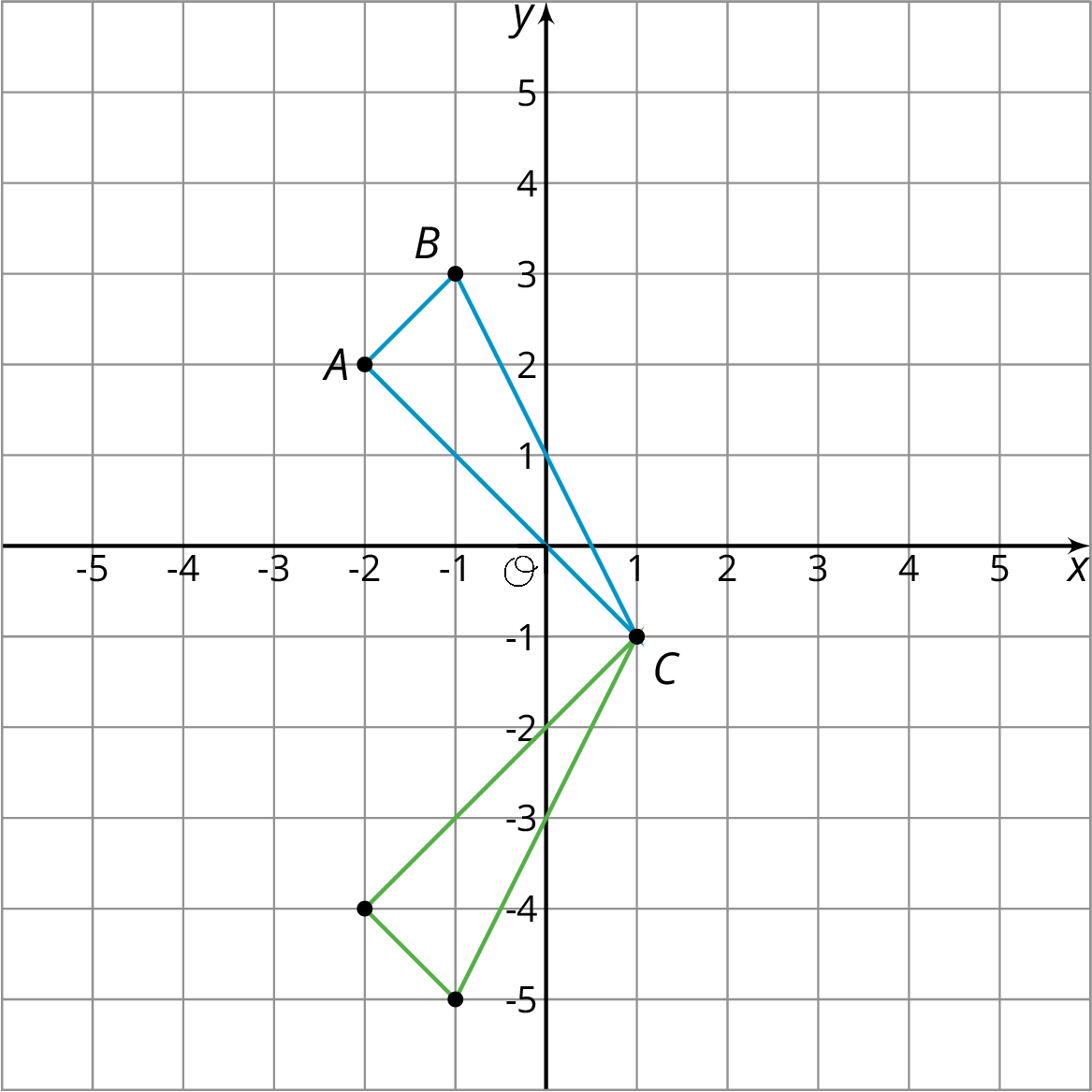
Here is triangle \(ABC\) reflected over the \(x\)-axis and then translated up two units.
Triangle \(ABC\) ends up in different places when the transformations are applied in the opposite order!