Lesson 15

Adding the Angles in a Triangle

View Student Lesson

Problem 1

In triangle \(ABC\), the measure of angle \(A\) is \(40^\circ\).

  1. Give possible measures for angles \(B\) and \(C\) if triangle \(ABC\) is isosceles.
  2. Give possible measures for angles \(B\) and \(C\) if triangle \(ABC\) is right.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

For each set of angles, decide if there is a triangle whose angles have these measures in degrees:

  1. 60, 60, 60
  2. 90, 90, 45
  3. 30, 40, 50
  4. 90, 45, 45
  5. 120, 30, 30

If you get stuck, consider making a line segment. Then use a protractor to measure angles with the first two angle measures.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Angle \(A\) in triangle \(ABC\) is obtuse. Can angle \(B\) or angle \(C\) be obtuse? Explain your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

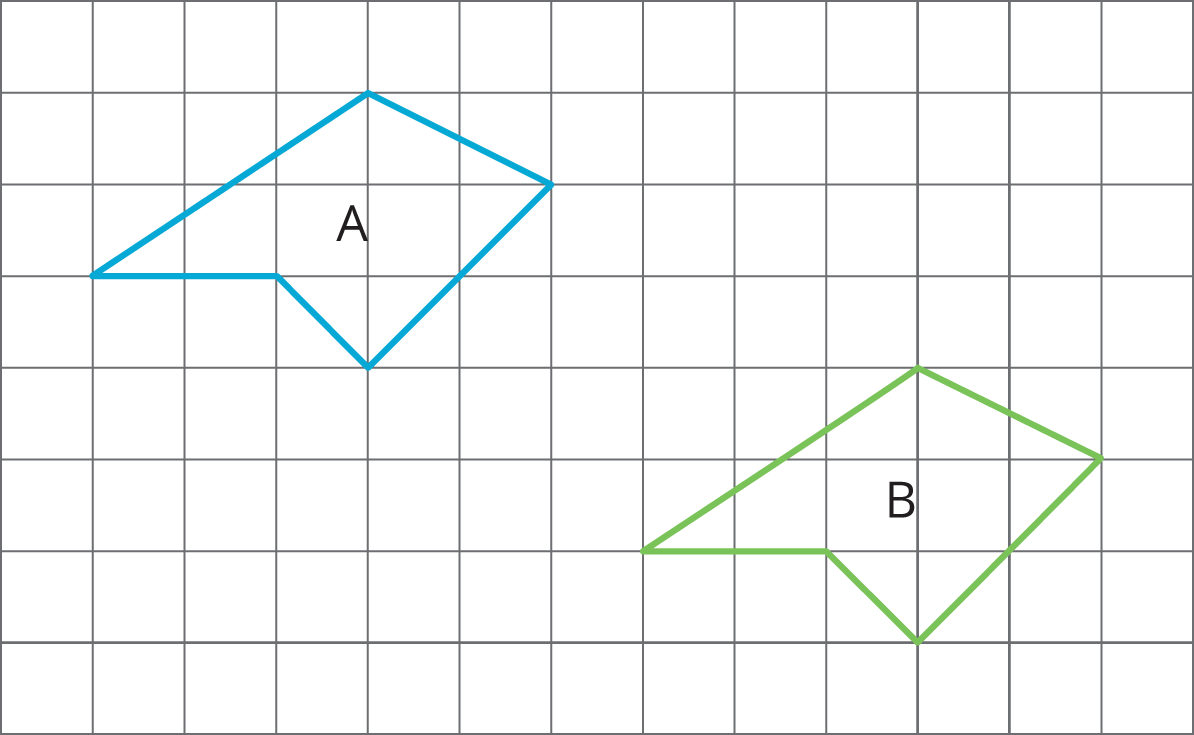
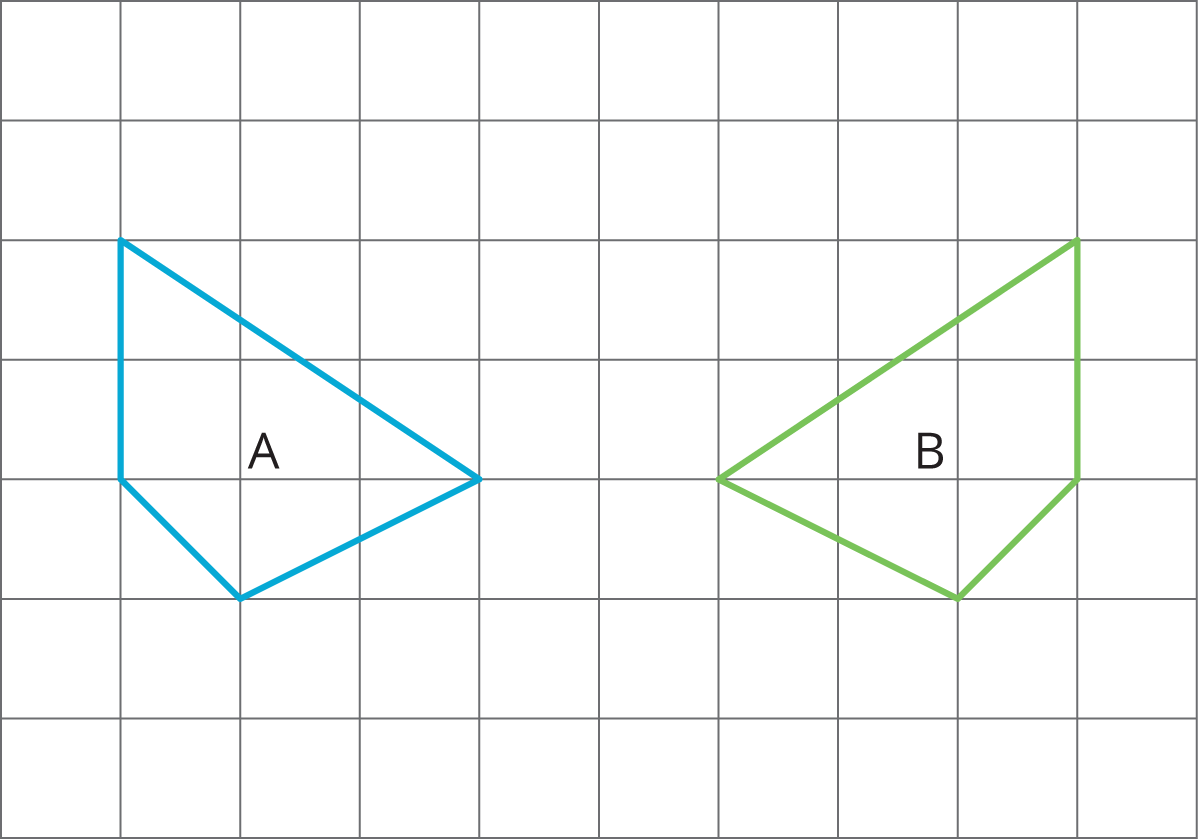
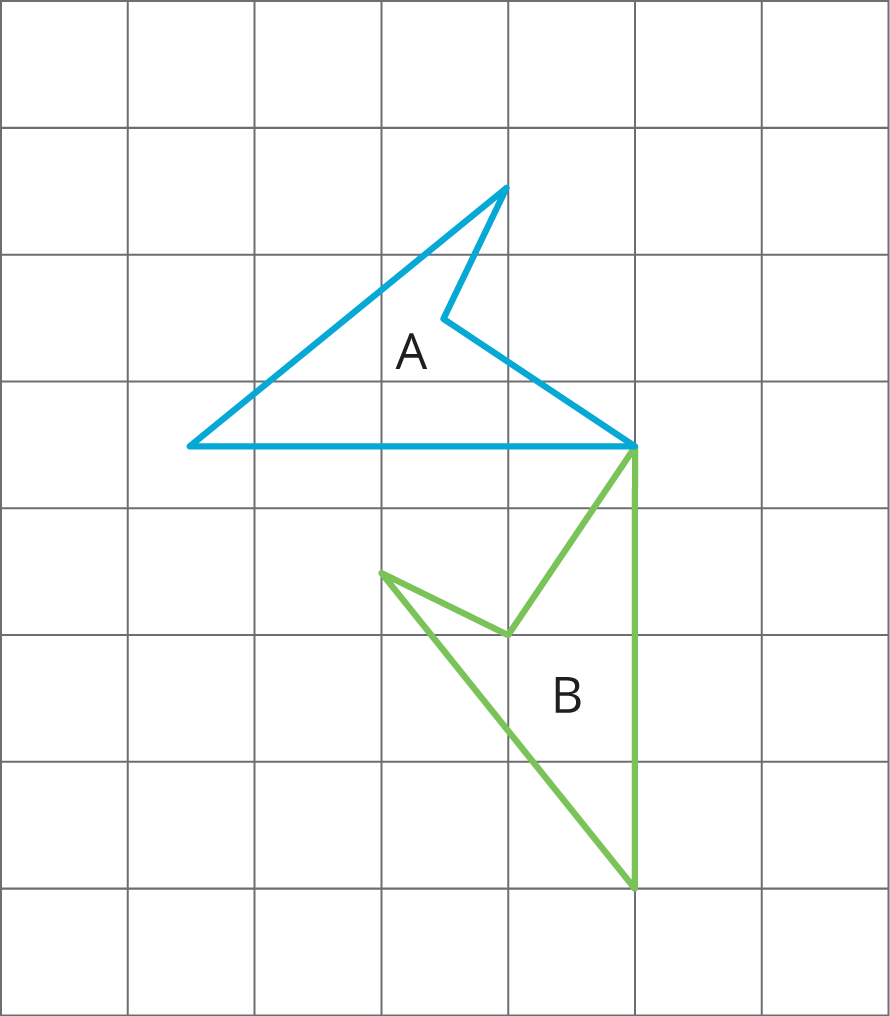
For each pair of polygons, describe the transformation that could be applied to Polygon A to get Polygon B.

  1. Two figures, polygon A and polygon B on a grid. Every point of polygon B is down 3 units and right 6 units from polygon A.
  2. Two figures, polygon A and polygon B on a grid. Every point of polygon B is a reflection of polygon A.
  3. Two figures, polygon A and polygon B on a grid. Every point of polygon B is a rotation of polygon A.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 3.)

Problem 5

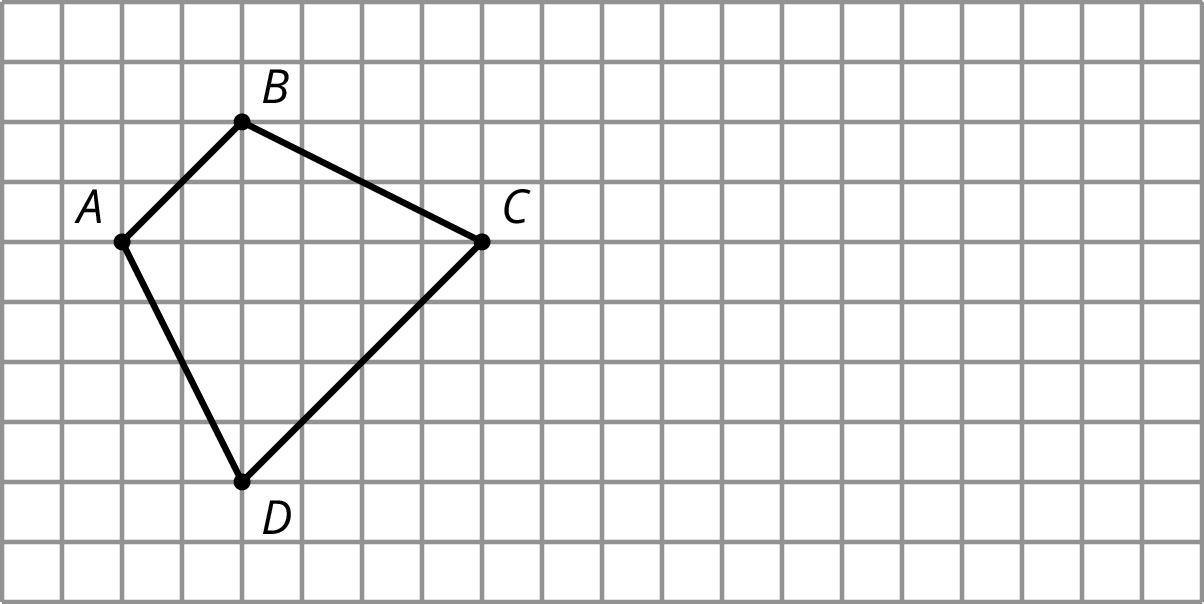
On the grid, draw a scaled copy of quadrilateral \(ABCD\) using a scale factor of \(\frac12\).

A quadrilateral on a grid.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 14.)