Lesson 2
Naming the Moves
2.1: A Pair of Quadrilaterals (10 minutes)
Warm-up
Students estimate an angle of rotation. While they do not need to use a protractor, a protractor is an ideal tool and allows them to estimate the angle measure more accurately. Monitor for how students report the measure of the angle: do they round to the nearest degree, to the nearest 5 degrees?
Launch
Arrange students in groups of 2–4. Provide access to geometry toolkits. Display the two quadrilateral figures for all to see. (They should also look at the task statement in their workbooks.) Ask students to give a discreet hand signal when they have an estimate for the angle of rotation. Give students 2 minutes of quiet think time and then time to share their thinking with their group before a whole-class discussion.
Student Facing
Quadrilateral A can be rotated into the position of Quadrilateral B.
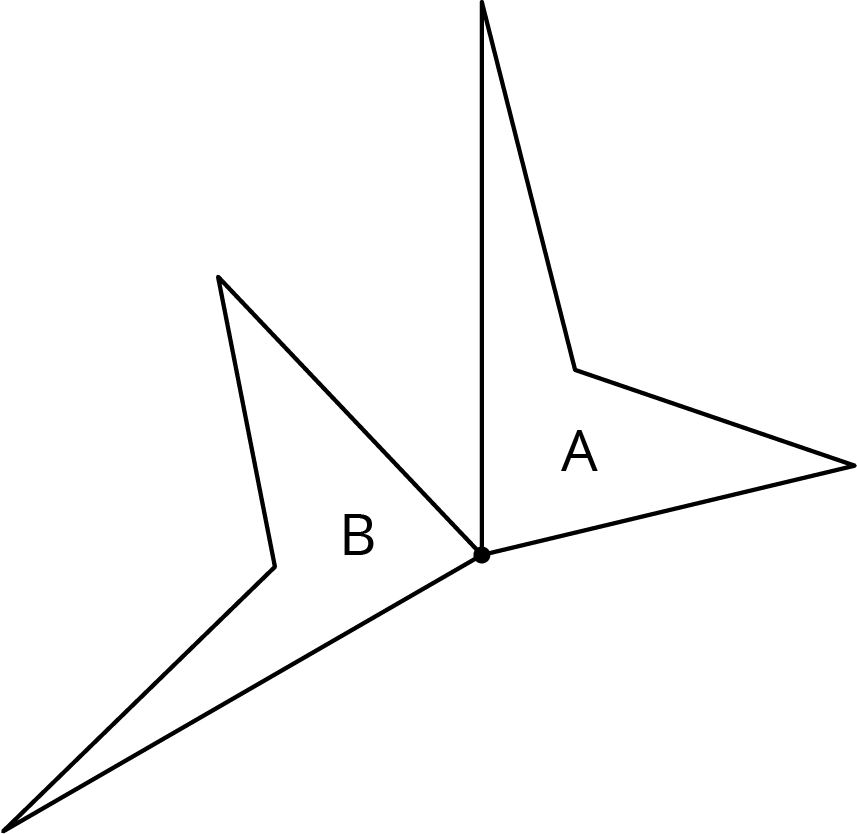
Estimate the angle of rotation.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not be sure which angle to measure. They may measure the acute angle between Shape A and Shape B. Ask these students to trace Shape A on tracing paper and rotate it by that angle to see that this does not give Shape B.
Activity Synthesis
Invite students to share their estimates for the angle of rotation. Ask students how they knew, for example, that the angle is more than 90 degrees (because the angle is obtuse) but less than 180 degrees (because the angle is less than a straight line).
Introduce or reiterate the language of clockwise (for rotating in the direction the hands on a clock move) and counterclockwise (for rotating in the opposite direction). In this case, the direction of rotation is not specified but it is natural to view Figure A being rotated counterclockwise onto Figure B. Make sure to introduce the language of the center of rotation (the vertex shared by A and B is the center of rotation).
It may be helpful to display the picture from the task statement to support this discussion, and if possible, show the \(120^\circ\) counterclockwise turn dynamically.
2.2: How Did You Make That Move? (10 minutes)
Activity
This activity informally introduces reflections, which appear in addition to some translations and rotations (that were introduced informally in the previous lesson). Students are given a 6-frame cartoon showing the change in position of a polygon. As in the previous lesson, they describe the moves, but this time there are reflections, which may seem impossible as physical moves unless you allow the shape to leave the plane. Students identify the new moves and try to describe them.
After the end of this activity, the three basic moves have been introduced and the next activity will introduce their names (translations, rotations, and reflections).
Launch
Keep students in the same groups, and maintain access to geometry toolkits. Give students 5 minutes of quiet work time, and then invite them to share their responses with their group. Follow with a whole-class discussion. Tell students that they will be describing moves as they did in the previous lesson, but this time there is a new move to look out for. Recall the words the class used to describe slides and turns.
Supports accessibility for: Conceptual processing; Language
Student Facing
Here is another set of dance moves.
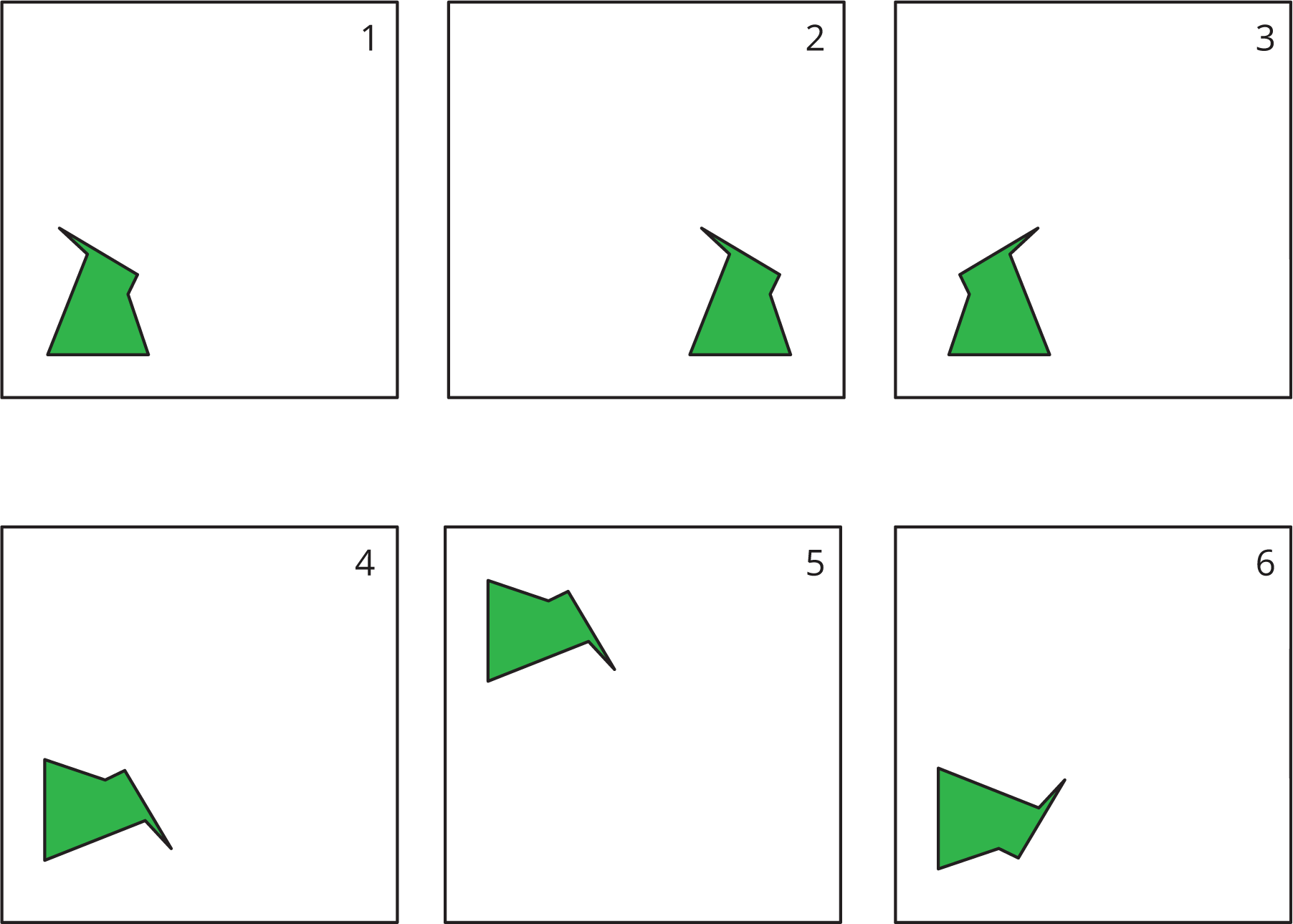
-
Describe each move or say if it is a new move.
-
Frame 1 to Frame 2.
-
Frame 2 to Frame 3.
-
Frame 3 to Frame 4.
-
Frame 4 to Frame 5.
-
Frame 5 to Frame 6.
-
-
How would you describe the new move?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may see a reflection as a translation especially since the figures are not on the same frame. Ask these students to trace Frame 2 on tracing paper. Is there any way to turn it into Frame 3 by sliding it? What do they have to do to turn it into Frame 3? (They have to flip the tracing paper over, so, this is a new kind of move.)
In describing reflections, students may confuse the terms horizontal and vertical. Consider posting the terms horizontal and vertical with examples in your room.
Activity Synthesis
The purpose of this discussion is an initial understanding that there is a third type of move that is fundamentally different from the moves encountered in the previous lesson, because it reverses directions. Some possible discussion questions to help them identify these are:
- “How is the motion from panel 2 to panel 3 different than the ones we discussed yesterday?”
- “Is there anywhere else that happens in this cartoon?”
- “What features of the image help us to see that this move is happening?”
To help answer these questions, tell students to pay attention to the direction that the “beak” of the polygon is pointing, left or right. Draw a dotted vertical line in the middle of Frame 2, and say, “Here is a mirror. The polygon in Frame 3 is what the polygon in Frame 2 sees when it looks in the mirror.”

Demonstrate using tracing paper or transparencies to show they are mirror images. Then ask students if there are any other mirror lines in other frames. For the second reflection, from Frame 5 to Frame 6, point out that the mirror line is now a horizontal line: in Frame 5 the beak is pointing down, and in Frame 6 the beak is pointing up, with the head on the right of the body in both cases. Contrast this with a rotation through 180º, which would put the head on the left of the body. Demonstrate with tracing paper or transparencies.
2.3: Card Sort: Move (15 minutes)
Activity
The purpose of this card sort activity is to give students further practice identifying translations, rotations, and reflections, and in the discussion after they have completed the task, introduce those terms. In groups of 3 they sort 9 cards into categories. There are 3 translations, 3 rotations, and 3 reflections. Students explain their categories and come to agreement on them.
On the blackline master, there are actually 12 cards. The last three show slightly more complicated moves than the first 9. These can be withheld, at first, and used if time permits.
Students might identify only 2 categories, putting the reflections with the translations (in the case of Card 3) or the rotations (in the case of Card 5). As students work, monitor for groups who have sorted the cards into translations, rotations, and reflections (though not necessarily using those words). Also monitor for descriptions of corresponding points such as “these points go together” or “here are before and after points.”
Launch
Arrange students into groups of 3, and provide access to geometry toolkits. Give each group the first 9 cards. Reserve the last 3 cards for use if time permits.
Tell students that their job is to sort the cards into categories by the type of move that they show. After they come to consensus about which categories to use, they take turns placing a card into a category and explaining why they think their card goes in that category. When it is not their turn, their job is to listen to their partner's reasoning and make sure they understand. Consider conducting a short demonstration with a student of productive ways to communicate during this activity. For example, show what it looks like to take turns, explain your thinking, and listen to your partner's thinking.
Give students about 10 minutes to sort the cards. Do not explicitly instruct students at the beginning to use the words translations, rotations, and reflections. Monitor for a group who uses these categories, even if they use different names for them. If time permits, distribute the remaining 3 cards. Follow with whole-class discussion.
If using the digital activity, ask the students to close their devices, at first. After they have come to agreement about how their cards should be sorted, they can open their devices and use the applets to help them refine the way they describe the moves.
Supports accessibility for: Language; Social-emotional skills
Student Facing
Your teacher will give you a set of cards. Sort the cards into categories according to the type of move they show. Be prepared to describe each category and why it is different from the others. You can explore the applets below to see the ways the images move.
Drag the red point. Explore how the image changes.
Click on the box to show the transformed image. Move the yellow points and the red segment to see how the image changes.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students into groups of 3, and provide access to geometry toolkits. Give each group the first 9 cards. Reserve the last 3 cards for use if time permits.
Tell students that their job is to sort the cards into categories by the type of move that they show. After they come to consensus about which categories to use, they take turns placing a card into a category and explaining why they think their card goes in that category. When it is not their turn, their job is to listen to their partner's reasoning and make sure they understand. Consider conducting a short demonstration with a student of productive ways to communicate during this activity. For example, show what it looks like to take turns, explain your thinking, and listen to your partner's thinking.
Give students about 10 minutes to sort the cards. Do not explicitly instruct students at the beginning to use the words translations, rotations, and reflections. Monitor for a group who uses these categories, even if they use different names for them. If time permits, distribute the remaining 3 cards. Follow with whole-class discussion.
If using the digital activity, ask the students to close their devices, at first. After they have come to agreement about how their cards should be sorted, they can open their devices and use the applets to help them refine the way they describe the moves.
Supports accessibility for: Language; Social-emotional skills
Student Facing
Your teacher will give you a set of cards. Sort the cards into categories according to the type of move they show. Be prepared to describe each category and why it is different from the others.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle to differentiate between the three moves, confusing reflections with either translations or rotations. After they make their best decision, encourage these students to use tracing paper to justify their response. In Card 10, students may be confused when the translated figure overlaps the original. For Card 4, students may first think that this is a rotation (much like Cards 6 and 9). Encourage these students here to use tracing paper to check their answers.
Activity Synthesis
Select one or more groups to share the names of their categories. Select one or more groups to share how they sorted the cards into the categories. Ask the class if they disagree with any of the choices, and give students opportunities to justify their reasoning (MP3).
Introduce the terms translation, rotation, and reflection. It may be helpful to display an example of each to facilitate discussion:

- Translation: ggbm.at/wYYvZH7A
- Rotation: ggbm.at/RUtdpQmN
- Reflection: ggbm.at/nKQmSnDW
Point out ways to identify which type of move it is. Translations are a slide with no turning. Rotations are a turn. Reflections face the opposite direction. If desired, introduce the terms image and corresponding points. If we see the figures as rabbits, then the ear tips in the original figure and the ear tips in its image are corresponding points, for example. The image is the figure after a transformation is applied: for each of the cards, one figure is the image of the other figure after a translation, rotation, or reflection has been applied.
Design Principle(s): Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
Questions for discussion:
- “We encountered a new type of move that was different from yesterday. What can you tell me about it?” (It's like a mirror image, you can't make the move by sliding or turning, the figure faces the opposite direction.)
- “We gave mathematical names to the three types of moves we have seen. What are they called?” (The “slide” is called a translation, the “turn" is called a rotation, and the mirror image is called a reflection.)
Consider creating a semi-permanent display that shows these three terms and their definitions for reference throughout the unit.
A translation slides a figure without turning it. Every point in the figure goes the same distance in the same direction. For example, Figure A was translated down and to the left, as shown by the arrows. Figure B is a translation of Figure A.
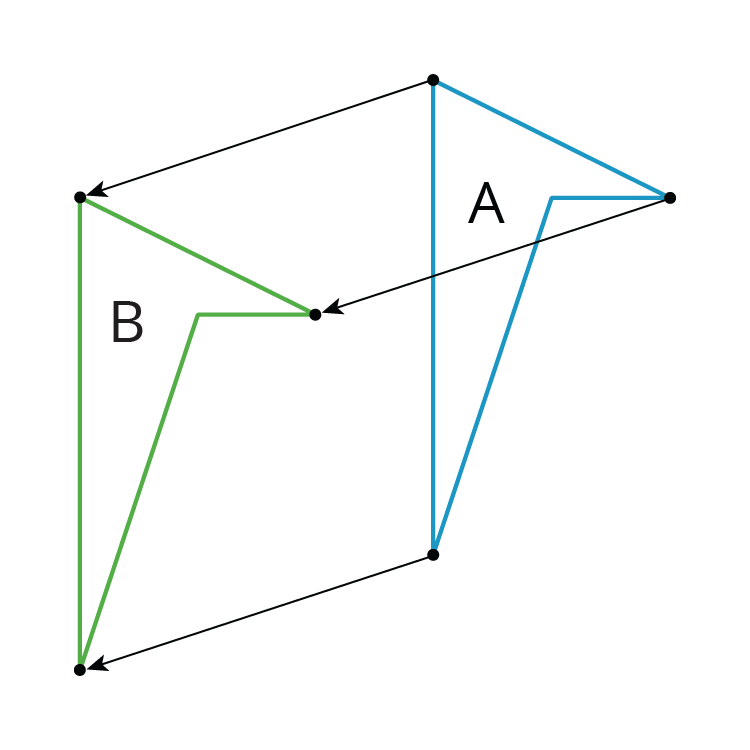
A rotation turns a figure about a point, called the center of the rotation. Every point on the figure goes in a circle around the center and makes the same angle. The rotation can be clockwise, going in the same direction as the hands of a clock, or counterclockwise, going in the other direction. For example, Figure A was rotated \(45^\circ\) clockwise around its bottom vertex. Figure C is a rotation of Figure A.

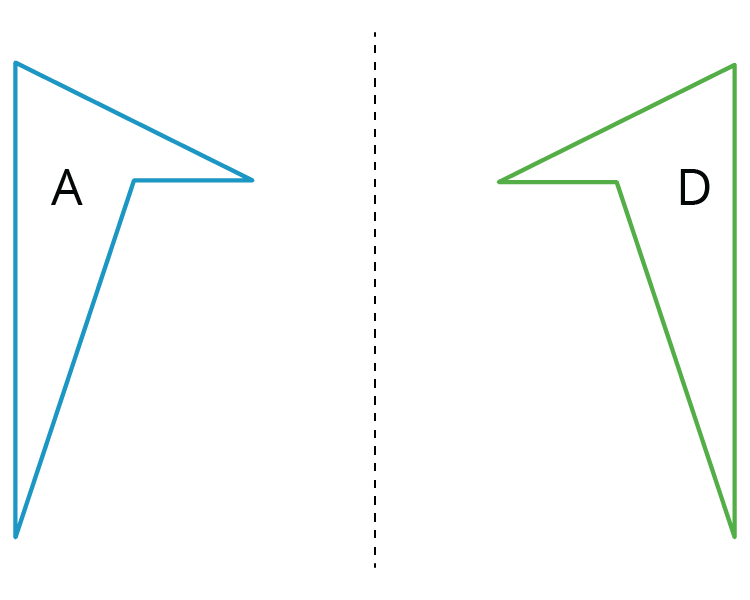
A reflection places points on the opposite side of a reflection line. The mirror image is a backwards copy of the original figure. The reflection line shows where the mirror should stand. For example, Figure A was reflected across the dotted line. Figure D is a reflection of Figure A.
2.4: Cool-down - Is It a Reflection? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here are the moves we have learned about so far:
-
A translation slides a figure without turning it. Every point in the figure goes the same distance in the same direction. For example, Figure A was translated down and to the left, as shown by the arrows. Figure B is a translation of Figure A.

-
A rotation turns a figure about a point, called the center of the rotation. Every point on the figure goes in a circle around the center and makes the same angle. The rotation can be clockwise, going in the same direction as the hands of a clock, or counterclockwise, going in the other direction. For example, Figure A was rotated \(45^\circ\) clockwise around its bottom vertex. Figure C is a rotation of Figure A.

-
A reflection places points on the opposite side of a reflection line. The mirror image is a backwards copy of the original figure. The reflection line shows where the mirror should stand. For example, Figure A was reflected across the dotted line. Figure D is a reflection of Figure A.

We use the word image to describe the new figure created by moving the original figure. If one point on the original figure moves to another point on the new figure, we call them corresponding points.