Lesson 7
No Bending or Stretching
7.1: Measuring Segments (5 minutes)
Warm-up
In this warm-up, students measure four line segments. They discuss the different aspects of making and recording accurate measurements. It is important to highlight the fractional markings and fraction and decimal equivalents used as students explain how they determined the length of the segment.
Launch
Give students 2 minutes of quiet work time followed by whole-class discussion.
Student Facing
For each question, the unit is represented by the large tick marks with whole numbers.
- Find the length of this segment to the nearest \(\frac18\) of a unit.

- Find the length of this segment to the nearest 0.1 of a unit.

- Estimate the length of this segment to the nearest \(\frac18\) of a unit.
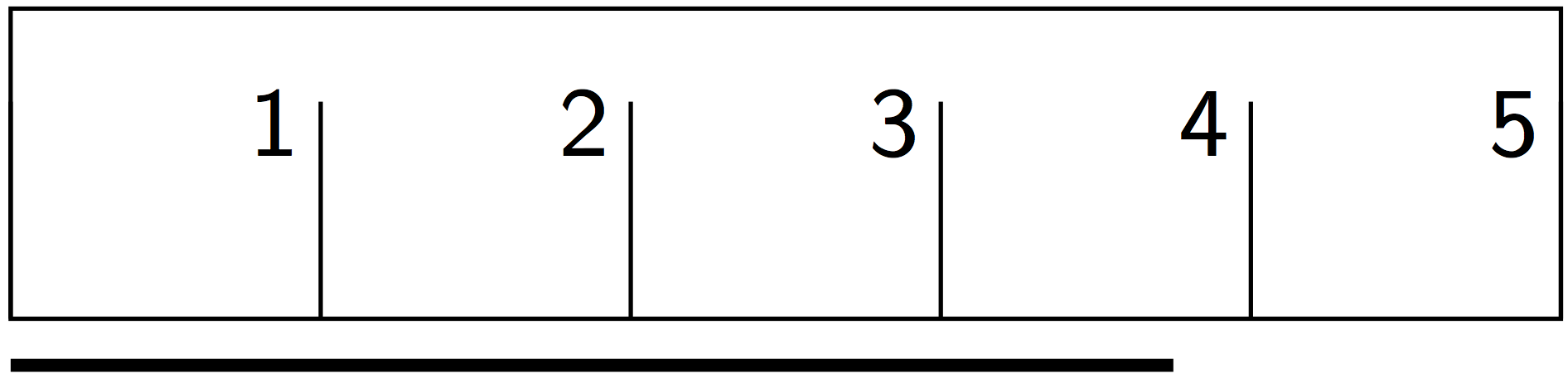
-
Estimate the length of the segment in the prior question to the nearest 0.1 of a unit.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle with the ruler that is not pre-partitioned into fractional units. Encourage these students to use what they know about eighths and tenths to partition the ruler and estimate their answer.
Activity Synthesis
Invite students to share their responses and record them for all to see. Ask the class if they agree or disagree with each response. When there is a disagreement, have students discuss possible reasons for the different measurements.
Students are likely to have different answers for their measure of the third segment. The ruler shown is not as accurate as the question requires as it has not been pre-partitioned into fractional units. Ask 2–3 students with different answers to share their strategies for measuring the third segment. There will be opportunities for students to use measuring strategies later in this lesson.
7.2: Sides and Angles (15 minutes)
Activity
The purpose of this activity is for students to see that translations, rotations, and reflections preserve lengths and angle measures. Students can use tracing paper to help them draw the figures and make observations about the preservation of side lengths and angle measures under transformations. While the grid helps measure lengths of horizontal and vertical segments, the students may need more guidance when asked to measure diagonal lengths. It is important in the launch to demonstrate for students how to either use the tracing paper or an index card to mark off unit lengths using the grid (MP5).
Since students are creating their own measuring tool, they can only give an estimate, and some flexibility should be allowed in the response. During the discussion, highlight different reasonable answers that students find for the lengths which are not whole numbers.
As students work individually, monitor and ask them to explain how they are performing their transformations and finding the side lengths and angle measures. During the discussion, select students who mention corresponding sides and angles, which they learned in grade 7 when making scaled copies, to share. Also select students who estimated the side lengths for Figure C correctly using either the tracing paper or index card.
Launch
Tell students, “In this activity you will be performing transformations. You can use tracing paper to help you draw the images of the figures or to check your work.”
Point students to Figure C and tell them, “When you are asked to measure side lengths here, you will need to make a ruler on either tracing paper or on a blank edge of an index card.” This reinforces the strategies and estimates students made in the warm-up.
Give students 3 minutes of quiet think time. Be sure to save at least 5 minutes for the discussion.
For classrooms using the digital version of the activity, the applets contain tools for the three rigid transformations students need. They have to choose which tool to use in each problem. Caution students that a quick click is all that is needed to select a figure. If they move the cursor away, and the image does not seem “highlighted,” it is likely they selected and de-selected the figure.
Supports accessibility for: Memory; Organization
Student Facing
- Translate Polygon \(A\) so point \(P\) goes to point \(P'\). In the image, write in the length of each side, in grid units, next to the side using the draw tool.
- Rotate Triangle \(B\) 90 degrees clockwise using \(R\) as the center of rotation. In the image, write the measure of each angle in its interior using the draw tool.
- Reflect Pentagon \(C\) across line \(\ell\).
- In the image, write the length of each side, in grid units, next to the side.
- In the image, write the measure of each angle in the interior.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Tell students, “In this activity you will be performing transformations. You can use tracing paper to help you draw the images of the figures or to check your work.”
Point students to Figure C and tell them, “When you are asked to measure side lengths here, you will need to make a ruler on either tracing paper or on a blank edge of an index card.” This reinforces the strategies and estimates students made in the warm-up.
Give students 3 minutes of quiet think time. Be sure to save at least 5 minutes for the discussion.
For classrooms using the digital version of the activity, the applets contain tools for the three rigid transformations students need. They have to choose which tool to use in each problem. Caution students that a quick click is all that is needed to select a figure. If they move the cursor away, and the image does not seem “highlighted,” it is likely they selected and de-selected the figure.
Supports accessibility for: Memory; Organization
Student Facing
- Translate Polygon \(A\) so point \(P\) goes to point \(Q\). In the image, write the length of each side, in grid units, next to the side.
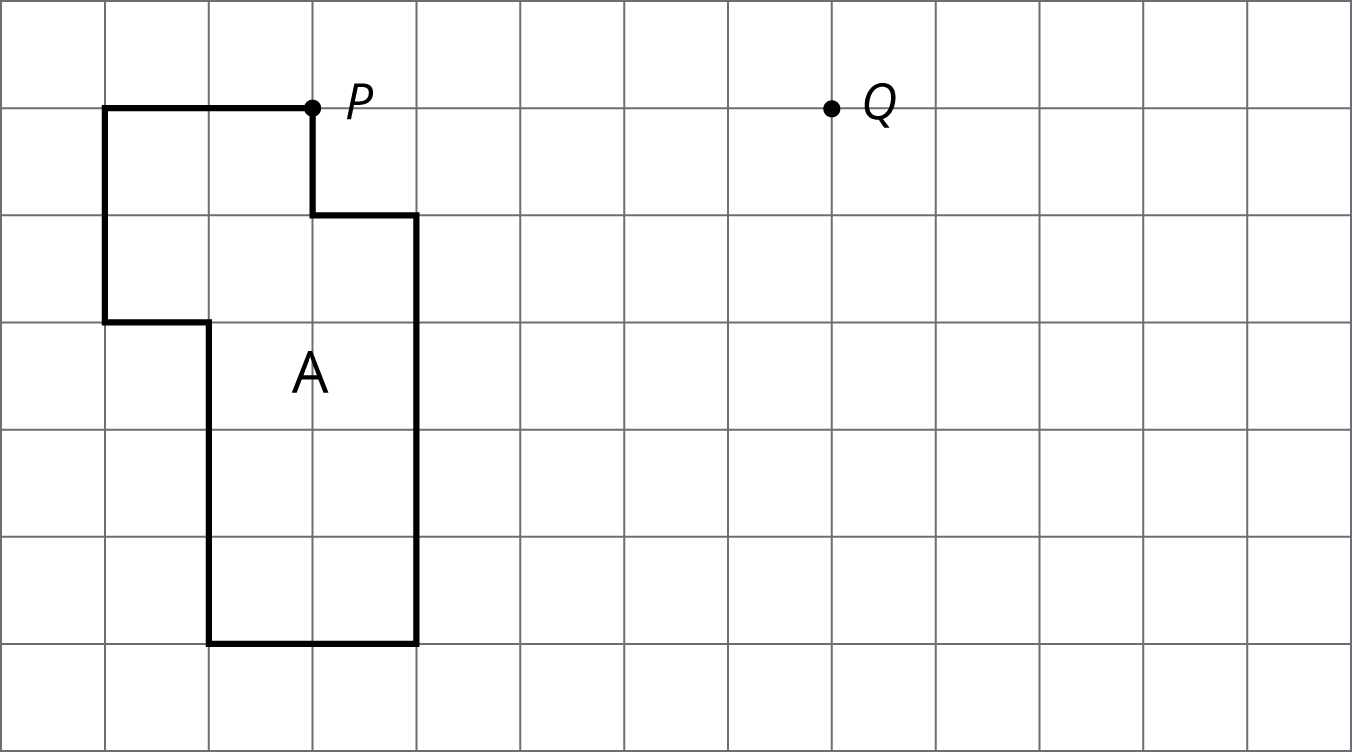
- Rotate Triangle \(B\) 90 degrees clockwise using \(R\) as the center of rotation. In the image, write the measure of each angle in its interior.

- Reflect Pentagon \(C\) across line \(\ell\).
-
In the image, write the length of each side, in grid units, next to the side. You may need to make your own ruler with tracing paper or a blank index card.
-
In the image, write the measure of each angle in the interior.

-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may try to count the grid squares on the diagonal side lengths. Remind students to measure these lengths with their tracing paper or index card. Students may also struggle estimating the diagonal side lengths on their self-marked index card or tracing paper. Remind students of how they estimated the lengths for the questions in the warm-up where the ruler was not marked.
Activity Synthesis
Ask selected students to share how they performed the given transformation for each question. After each explanation, ask the class if they agree or disagree. Introduce students to the idea of corresponding sides and corresponding angles. Ask students to identify the corresponding angles in the first question and the corresponding side lengths in the second since they were not asked about these attributes the first time. The point here is not to find the actual values but to note that the corresponding measurements are equal. Since it is sometimes not possible to measure angles or side lengths exactly, student estimates for these values (both corresponding sides and corresponding angles) may be slightly different.
Point out that for each of the transformations in this activity, the lengths of the sides of the original figure equal the lengths of the corresponding sides in the image, and the measures of the angles in the original figure equal the measures of the corresponding angles in the image. For this reason, we call these transformations rigid transformations: they behave as if we are moving the shapes around without stretching, bending, or breaking them. An example of a non-rigid transformation is one that compresses a figure vertically, like this:
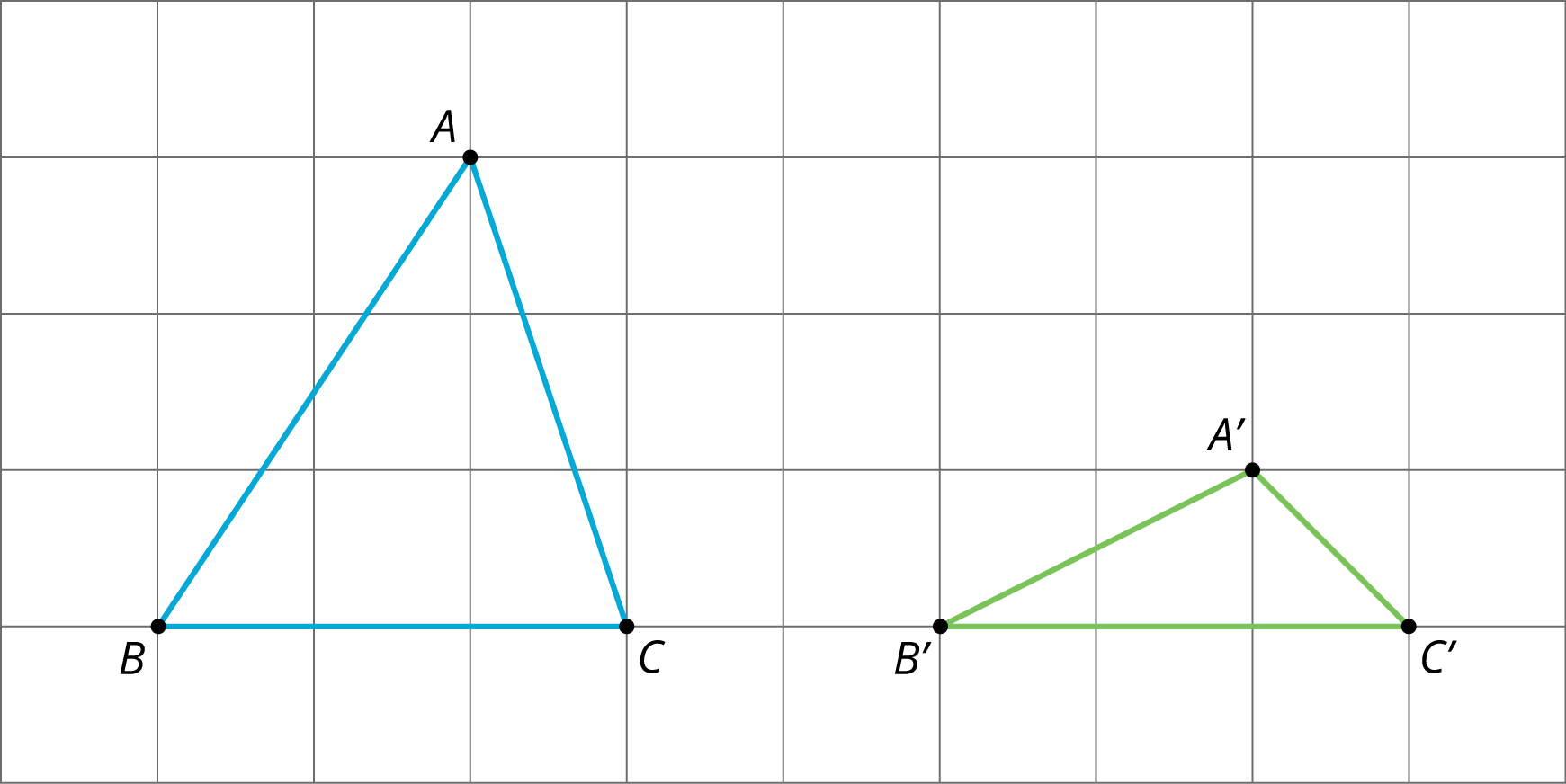
Tell them that a rigid transformation is a transformation where all pairs of corresponding distances and angle measures in the figure and its image are equal. It turns out that translations, reflections, and rotations are the building blocks for all rigid transformations, and we will explore that next.
Design Principle(s): Optimize output (for explanation)
7.3: Which One? (10 minutes)
Activity
The purpose of this activity is to decide if there is a sequence of translations, rotations, and reflections that take one figure to another and, if so, to produce one such sequence. Deciding whether or not such a sequence is possible uses the knowledge that translations, rotations, and reflections do not change side lengths or angle measures. The triangles \(ABC\) and \(CFG\) form part of a large pattern of images of triangle \(ABC\) that will be examined more closely in future lessons.
Monitor for students who use different transformations to take triangle \(ABC\) to triangle \(CFG\) and select them to share during the discussion. (There are two possible sequences in the Possible Responses section, but these are not the only two.)
Launch
Provide access to geometry toolkits. Give students 4 minutes quiet work time, 2 minutes to discuss with partner, and then time for a whole-class discussion.
If using the digital activity, have a brief discussion of the previous activity to highlight the transformations that the students used. Then give students 4 minutes of individual work time, 2 minutes to discuss with a partner, and then time for a whole-class discussion.
Supports accessibility for: Language; Organization
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Here is a grid showing triangle \(ABC\) and two other triangles.
You can use a rigid transformation to take triangle \(ABC\) to one of the other triangles.
-
Which one? Explain how you know.
-
Describe a rigid transformation that takes \(ABC\) to the triangle you selected.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Provide access to geometry toolkits. Give students 4 minutes quiet work time, 2 minutes to discuss with partner, and then time for a whole-class discussion.
If using the digital activity, have a brief discussion of the previous activity to highlight the transformations that the students used. Then give students 4 minutes of individual work time, 2 minutes to discuss with a partner, and then time for a whole-class discussion.
Supports accessibility for: Language; Organization
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Here is a grid showing triangle \(ABC\) and two other triangles.

You can use a rigid transformation to take triangle \(ABC\) to one of the other triangles.
-
Which one? Explain how you know.
-
Describe a rigid transformation that takes \(ABC\) to the triangle you selected.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A square is made up of an L-shaped region and three transformations of the region. If the perimeter of the square is 40 units, what is the perimeter of each L-shaped region?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask a student to explain why triangle \(ABC\) cannot be taken to triangle \(DBE\). (We are only using rigid transformations and therefore the corresponding lengths have to be equal and they are not.) If a student brings up that they think triangle \(DBE\) is a scale drawing of \(ABC\), bring the discussion back to translations, rotations, and reflections, rather than talking about how or why triangle \(DBE\) isn’t actually a scale drawing of \(ABC\).
Offer as many methods for transforming triangle \(ABC\) as possible as time permits, selecting previously identified students to share their methods. Include at least two different sequences of transformations. Make sure students attend carefully to specifying each transformation with the necessary level of precision. For example, for a rotation, that they specify the center of rotation, the direction, and the angle of rotation.
If time allows, consider asking the following questions:
- "Can triangle \(ABC\) be taken to triangle \(CFG\) with only a translation?" (No, since \(CFG\) is rotated.)
- "What about with only a reflection?" (No, because they have the same orientation.)
- "What about with a single rotation?" (The answer is yes, but this question does not need to be answered now as students will have an opportunity to investigate this further in a future lesson.)
Lesson Synthesis
Lesson Synthesis
Remind students that a rigid transformation is a transformation for which all pairs of corresponding lengths and angle measures in the original figure and its image are equal. Translations, rotations, and reflections have this property, so they are rigid transformations. Sequences of these are as well—for example, if you translate a figure then reflect the image, the side lengths and angle measures stay the same.
Ask students to think of ways they could look at two shapes and tell that one is not the image of the other under a rigid transformation. Give a moment of quiet think time, and then invite students to share their ideas (If two shapes have different side lengths or angle measures then there is no rigid transformation taking one shape to the other).
When there is a rigid transformation taking one figure to another, there are many ways to do this. Ask students:
- "What are some good ways to tell whether one shape can be taken to another with a sequence of rigid transformations?" (Measure all of the side lengths and angle measure and ensure that corresponding measurements are equal. Use tracing paper to see if one shape matches up exactly with the other.)
- "What are the three basic types of rigid transformations?" (rotations, translations, and reflections)
7.4: Cool-down - Translated Trapezoid (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The transformations we’ve learned about so far, translations, rotations, reflections, and sequences of these motions, are all examples of rigid transformations. A rigid transformation is a move that doesn’t change measurements on any figure.
Earlier, we learned that a figure and its image have corresponding points. With a rigid transformation, figures like polygons also have corresponding sides and corresponding angles. These corresponding parts have the same measurements.
For example, triangle \(EFD\) was made by reflecting triangle \(ABC\) across a horizontal line, then translating. Corresponding sides have the same lengths, and corresponding angles have the same measures.
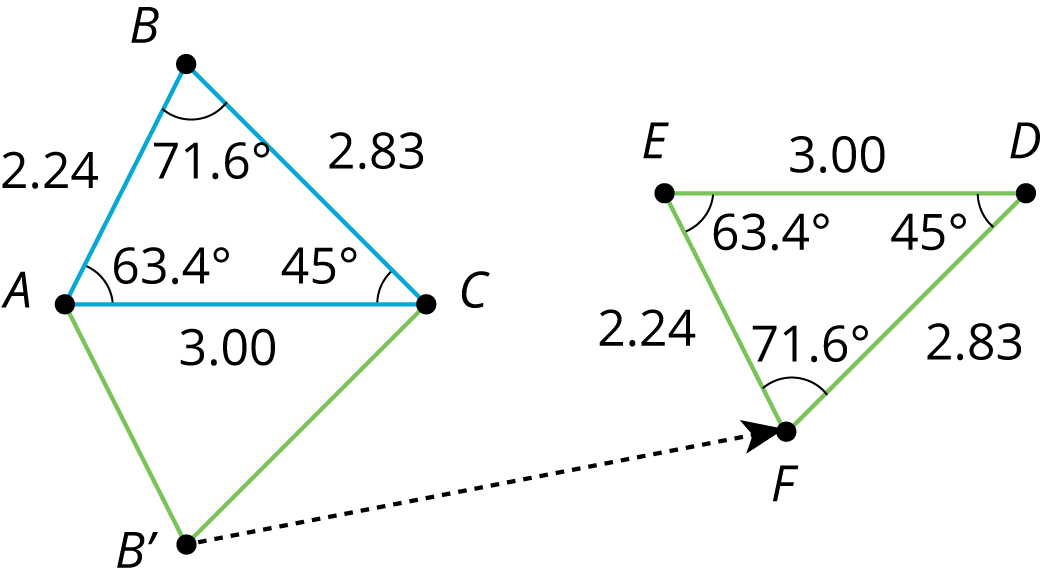
| measurements in triangle \(ABC\) | corresponding measurements in image \(EFD\) |
|---|---|
| \(AB = 2.24\) | \(EF = 2.24\) |
| \(BC = 2.83\) | \(FD = 2.83\) |
| \(CA = 3.00\) | \(DE = 3.00\) |
| \(m\angle ABC = 71.6^\circ\) | \(m\angle EFD= 71.6^\circ\) |
| \(m\angle BCA = 45.0^\circ\) | \(m\angle FDE= 45.0^\circ\) |
| \(m\angle CAB = 63.4^\circ\) | \(m\angle DEF= 63.4^\circ\) |