Lesson 4

Solving for Unknown Angles

View Student Lesson

Problem 1

\(M\) is a point on line segment \(KL\). \(NM\) is a line segment. Select all the equations that represent the relationship between the measures of the angles in the figure.

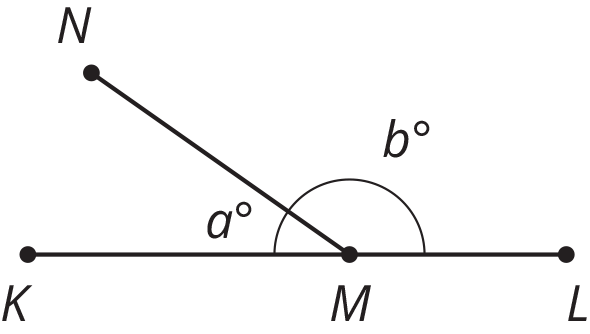
M is a point on line segment K L. Segment N M creates two angles, measure a, degrees and b degrees.
A:

\(a=b\)

B:

\(a+b=90\)

C:

\(b=90-a\)

D:

\(a+b=180\)

E:

\(180-a=b\)

F:

\(180=b-a\)

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Which equation represents the relationship between the angles in the figure?

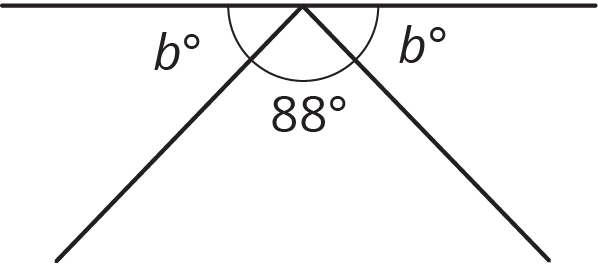
Two rays on the same side of a line meet at a point on the line to form 3 angles, with measure b degrees, 88 degrees, b degrees.
A:

\(88+b=90\)

B:

\(88+b=180\)

C:

\(2b+88=90\)

D:

\(2b+88=180\)

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Segments \(AB\), \(EF\), and \(CD\) intersect at point \(C\), and angle \(ACD\) is a right angle. Find the value of \(g\).

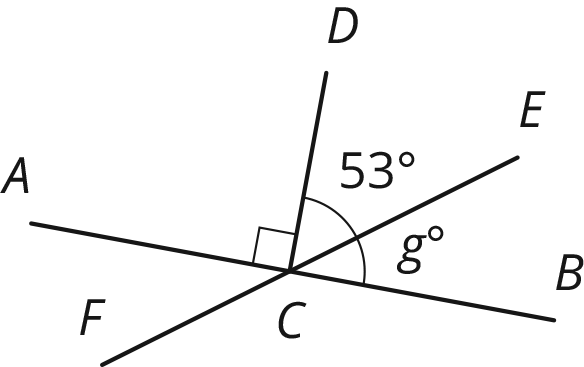
Segment A, B, segment E F, and segment C D intersect at point C. Clockwise, the endpoints are A, D, E, B, F. Angle A, C D is a right angle. Angle D C E is 53 degrees, angle E C B is g degrees.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Select all the expressions that are the result of decreasing \(x\) by 80%.

A:

\(\frac{20}{100}x\)

B:

\(x - \frac{80}{100}x\)

C:

\(\frac{100-20}{100}x\)

D:

\(0.80x\)

E:

\((1-0.8)x\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 12.)

Problem 5

Andre is solving the equation \(4(x+\frac32)=7\). He says, “I can subtract \(\frac32\) from each side to get \(4x=\frac{11}{2}\) and then divide by 4 to get \(x=\frac{11}{8}\).” Kiran says, “I think you made a mistake.”

  1. How can Kiran know for sure that Andre’s solution is incorrect?
  2. Describe Andre’s error and explain how to correct his work.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 8.)

Problem 6

Solve each equation.

\(\frac17a+\frac34=\frac98\)

\(\frac23+\frac15b=\frac56\)

\(\frac32=\frac43c+\frac23\)

\(0.3d+7.9=9.1\)

\(11.03=8.78+0.02e\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 7.)

Problem 7

A train travels at a constant speed for a long distance. Write the two constants of proportionality for the relationship between distance traveled and elapsed time. Explain what each of them means.

time elapsed (hr) distance (mi)
1.2 54
3 135
4 180

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 5.)