Lesson 12

Volume of Right Prisms

12.1: Three Prisms with the Same Volume (5 minutes)

The purpose of this warm-up is to encourage students to think about possible heights of prisms with the same height and volume based on the area of a base. This is a review of previous work students have done with volume in which they found the volume of a rectangular prism by multiplying the area of a base and height. The ideas in this warm-up are revisited later in this lesson, so it is important students can clearly explain how they ordered their prisms based on them having the same volume and how they found the height of the prism with base C.

Arrange students in groups of 2. Give students 1 minute of quiet work time followed by time to discuss their explanations with a partner. Follow with a whole-class discussion.

Rectangles A, B, and C represent bases of three prisms.

Three rectangles, A, B, C. Rectangle A is 1 square by 3 squares. Rectangle B is 2 squares by 2 squares. Rectangle C is 6 squares by 2 squares.

If each prism has the same height, which one will have the greatest volume, and which will have the least? Explain your reasoning.
If each prism has the same volume, which one will have the tallest height, and which will have the shortest? Explain your reasoning.

For access, consult one of our IM Certified Partners.

Select students to share the prism they found to have the greatest and least volume and the tallest and shortest height. Record and display their responses for all to see. Poll the class if they agree or disagree. If students all agree, ask a few students to share their reasoning. If they do not agree, ask students to share their reasoning until they reach an agreement.

If there is time, display this question for all to see: “If each prism has the same volume and the prism associated with base B has a height of 6 units, what is the height of the prism associated with base C?”

Have students share the volume of the prism with base C and their reasoning. Record and display the responses for all to see.

12.2: Finding Volume with Cubes (10 minutes)

In grades 5 and 6, students worked with the volume of rectangular prisms. In this activity, students extend their understanding to see that even when the base is not a rectangle, they can still calculate the volume of a prism by multiplying the area of the base times the height of the prism.

Students use snap cubes to build a prism with a base that matches the shape from the blackline master. Each group needs 30 snap cubes for the first question and a total of 60 snap cubes for the second question. If there are not enough snap cubes, two groups of 3 students may combine together after answering the first question to form one group of 6 students.

If using snap cubes that measure \(\frac34\) inch, make copies of the first page of the blackline master, with the slightly smaller shapes. If using snap cubes that measure 2 cm, make copies of the second page of the blackline master, with the slightly larger shapes.

Digital

Arrange students in groups of 3. Distribute copies of the blackline master, one half-page to each group, and 30–60 snap cubes to each group. Give students 2–3 minutes of quiet work time followed by a whole-class discussion.

For students using digital materials: depending on the needs of your class, either demonstrate how to build figures using the applet, or instruct students to read and follow the instructions for working the applet.

This applet has 64 snap cubes, all sitting in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. You can keep dragging blocks out of the pile by their red points until you have enough to build what you want.

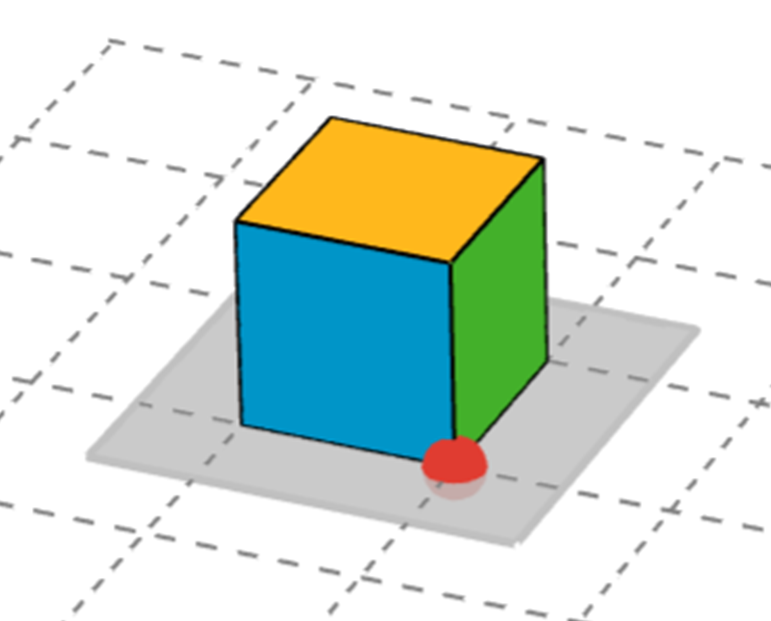
A snap cube sits on a grid, with a red point on one corner.

Click on the red points to change from left/right movement to up/down movement.

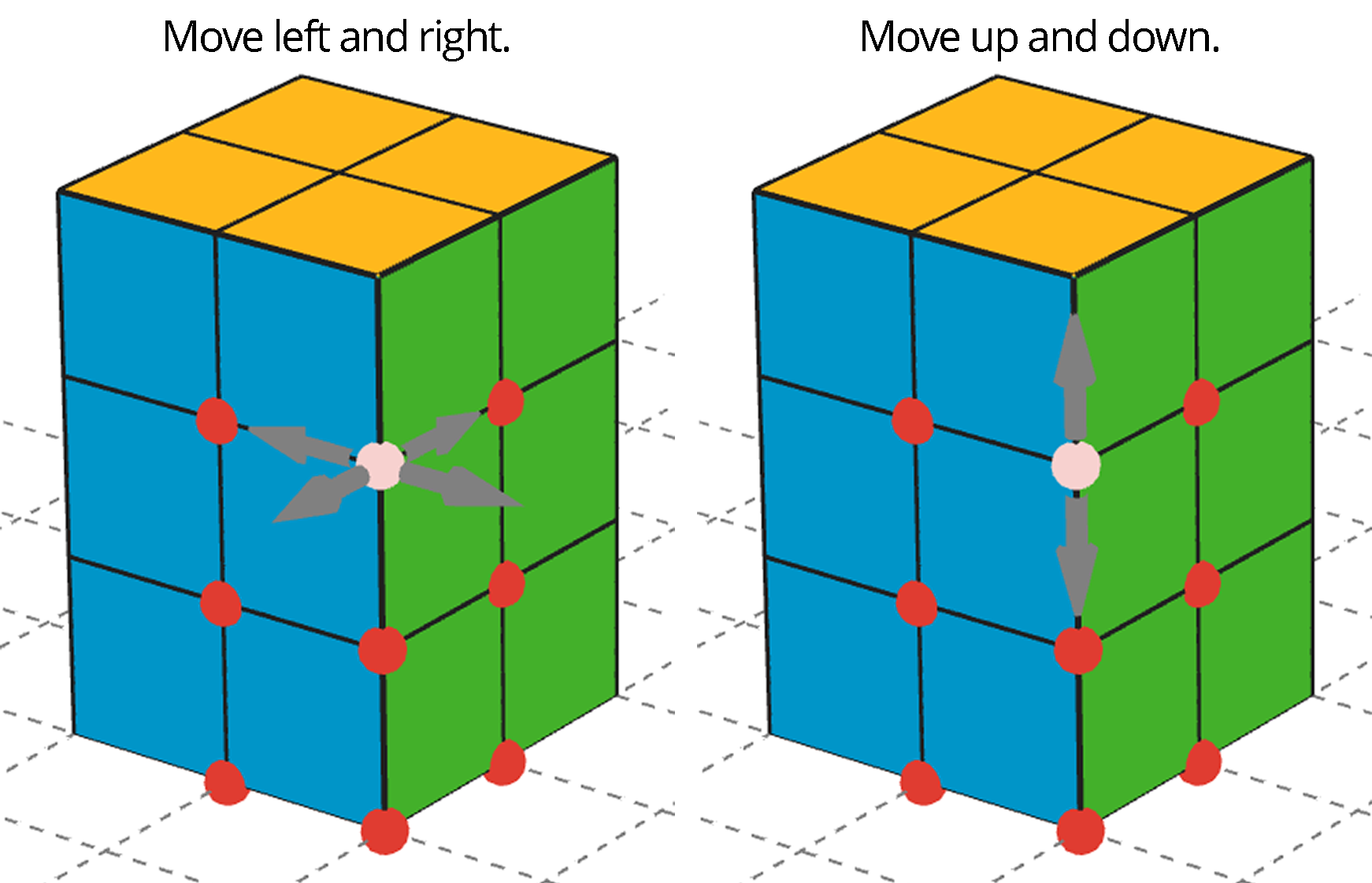
Two images, each stacks of snap cubes 2 by 2 by 3. On the first image, arrows indicate left and right motion. On the second image, arrow indicated up and down motion.

There is also a shape on the grid. It marks the footprint of the shapes you will be building.

Using the face of a snap cube as your area unit, what is the area of the shape? Explain or show your reasoning.
Use snap cubes to build the shape from the paper. Add another layer of cubes on top of the shape you have built. Describe this three-dimensional object.
What is the volume of your object? Explain your reasoning.
Right now, your object has a height of 2. What would the volume be
1. if it had a height of 5?
2. if it had a height of 8.5?

For access, consult one of our IM Certified Partners.

Your teacher will give you a paper with a shape on it and some snap cubes.

Using the face of a snap cube as your area unit, what is the area of the shape? Explain or show your reasoning.
Use snap cubes to build the shape from the paper. Add another layer of cubes on top of the shape you have built. Describe this three-dimensional object.
What is the volume of your object? Explain your reasoning.
Right now, your object has a height of 2. What would the volume be:
1. if it had a height of 5?
2. if it had a height of 8.5?

For access, consult one of our IM Certified Partners.

Select students to share their reasoning.

Consider asking some of the following questions:

“How do you know this figure is a prism?” (Cross sections parallel to the base are identical copies.)
“What is the area of the base of this figure?” (It is the number of cubes in one layer of the prism.)
“How do you calculate the total number of cubes to make the prism?” (Multiply the number of cubes in one layer by the number of layers.)
“What is the volume of this prism?” (The volume is the same as calculating the number of cubes to make the prism.)
“If you find the area of the base, how do you use that information to calculate the volume of the prism?” (Multiply the area of the base by the height of the prism.)
“How would the volume of the prism change if we changed the shape of the base but still used 27 cubes to build it?” (The volume would not change.)

If not mentioned by students, explain that calculating the total number of cubes to make the prism is the same as calculating the volume of the prism. We can find the area of the base of the prism and multiply that by the number of layers in the prism which is the same as the height of the prism. The height of the prism is measured in units, the area of the base is measured in units² and the volume of the prism is measured in units³.

Writing, Listening, Conversing: MLR1 Stronger and Clearer Each Time. Use this routine to help students improve their writing, by providing them with multiple opportunities to clarify their explanations through conversation. Invite students to draft an initial response to the question: “How do you know if a three-dimensional figure is a prism?” Give students time to meet with 2–3 partners, to share and get feedback on their responses. Provide students with prompts for feedback that will help their partner strengthen their ideas and clarify their language (e.g., “What are some properties of prisms?”, “Can you give an example and non-example?”, etc.). Students can borrow ideas and language from each partner to refine and clarify their explanation. This will also help students to build and describe the three-dimensional figures used in this lesson and the unit.
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness

12.3: Can You Find the Volume? (15 minutes)

The purpose of this activity is for students get hands-on experience with polyhedra, recognizing whether a figure is a prism and if so, determining which face is the base of the prism. Once students determine which face is the base, they use a ruler marked in inches to measure the height of the prism. The area of each face is labeled on the shape so that students do not get bogged down with calculating the base area and can focus on using the area to find the volume.

Instead of creating enough sets of polyhedra for every group to have one of every shape at the same time, consider having the students pass the shapes from one group to the next or rotate around to different stations so that fewer sets of shapes have to be constructed.

Digital

Arrange students in groups of 3–4. Distribute the three-dimensional figures that were already assembled from the nets in the blackline master and rulers marked in centimeters. Give students 1–2 minutes of quiet work time with the polyhedra given to their group, have groups exchange objects so that each group gets to examine each figure. Follow with a whole-class discussion.

Students using the digital version have an applet with the six polyhedra in 3D. Students can rotate the view using the tool marked by two intersecting, curved arrows. Note that each polyhedron has only one label per unique face. If no other measurements are shown, the faces are congruent. Students can use the distance tool, marked with the "cm," to find the height or length of any segment. Troubleshooting tip: the cursor must be on the 3D Graphics window for the full toolbar to appear.

The applet has a set of three-dimensional figures.

For each figure, determine whether the shape is a prism.
For each prism:
1. Find the area of the base of the prism.
2. Find the height of the prism.
3. Calculate the volume of the prism.

Is it a prism?	area of prism base (cm²)	height (cm)	volume (cm³)

Begin by grabbing the gray bar on the left and dragging it to the right until you see the slider.
Choose a figure using the slider.
Rotate the view using the Rotate 3D Graphics tool marked by two intersecting, curved arrows.
Note that each polyhedron has only one label per unique face. Where no measurements are shown, the faces are identical copies.
Use the distance tool, marked with the "cm," to click on any segment and find the height or length.
Troubleshooting tip: the cursor must be on the 3D Graphics window for the full toolbar to appear.

For access, consult one of our IM Certified Partners.

Students using the digital version have an applet with the five polyhedra in 3D. Students can rotate the view using the tool marked by two intersecting, curved arrows. Note that each polyhedron has only one label per unique face. If no other measurements are shown, the faces are congruent. Students can use the distance tool, marked with the "cm," to find the height or length of any segment. Troubleshooting tip: the cursor must be on the 3D Graphics window for the full toolbar to appear.

Your teacher will give you a set of three-dimensional figures.

For each figure, determine whether the shape is a prism.
For each prism:
1. Find the area of the base of the prism.
2. Find the height of the prism.
3. Calculate the volume of the prism.

	Is it a prism?	area of prism base (cm²)	height (cm)	volume (cm³)
figure A
figure B
figure C
figure D
figure E
figure F

For access, consult one of our IM Certified Partners.

Are you ready for more?

Imagine a large, solid cube made out of 64 white snap cubes. Someone spray paints all 6 faces of the large cube blue. After the paint dries, they disassemble the large cube into a pile of 64 snap cubes.

How many of those 64 snap cubes have exactly 2 faces that are blue?
What are the other possible numbers of blue faces the cubes can have? How many of each are there?
Try this problem again with some larger-sized cubes that use more than 64 snap cubes to build. What patterns do you notice?

For access, consult one of our IM Certified Partners.

Some students may say that Figure A is not a prism because it is a cube. Ask them whether the cross sections would be identical if you made various cuts parallel to one side. Explain that a cube is a special type of square prism where the height of the prism matches the side lengths of the base. Consider making a comparison to the fact that a square is a special type of rectangle.

Poll the class for answers to the first column of the table. Make sure the class agrees about answers before proceeding. Select students to provide their answers to each part of the table and an explanation. Display answers on the table for all to see. Ask students:

“What is different about the structure of non-prisms in comparison to prisms?" (The prisms have multiple layers of the same base, where the non-prism does not have that.)
“Why can’t you use ‘area of the base times the height’ to calculate the volume of the figures that were not prisms?" (Because the non-prism isn't made up of multiple layers of the same base.)

Writing, Speaking: MLR3 Clarify, Critique, Correct. Use this routine to support student reasoning about whether a figure is a prism or not. Before students share their answers, display an incorrect answer showing conceptual (or common) errors. For example, “Figure A is not a prism because it is a cube.” or “Figure B is a prism because its base is a rectangle.” Ask students to work with a partner to identify the errors and critique the reasoning shown. Provide questions for discussion such as, “What is unclear?” or “Are there any errors?” Give students 2–3 minutes of quiet time to revise the original statement, by drawing on the conversations with their partners. Improved statements should draw on properties of prisms, such as: cross sections are parallel to the base and are identical copies. This will facilitate students’ understanding of prisms and their ability to evaluate, and improve on, the written mathematical arguments of others.
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness

12.4: What’s the Prism’s Height? (10 minutes)

The purpose of this activity is for students to work backwards from the volume to the height of a prism. Students see that for two prisms to have the same volume, the one with the smaller base has the taller height and the one with the larger base has the shorter height. The grid helps students find the area of the base so they can focus their attention on what it means to have a prism made out of stacks of layers of the same base.

Arrange students in groups of 2. Give students 5 minutes of quiet work time followed by time to discuss their thinking with a partner. Follow with a whole-class discussion.

Representation: Develop Language and Symbols. Use virtual or concrete manipulatives to connect symbols to concrete objects or values. Provide students with geometric solids or snap cubes and a printed copy of the student task statement to draw on or annotate.
Supports accessibility for: Conceptual processing

There are 4 different prisms that all have the same volume. Here is what the base of each prism looks like.

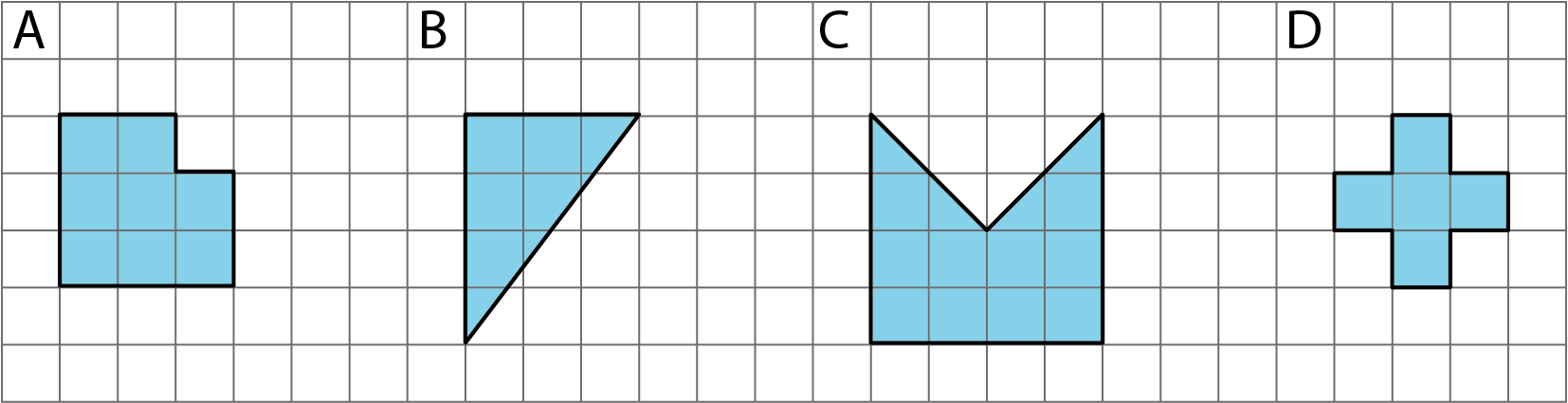
Order the prisms from shortest to tallest. Explain your reasoning.
If the volume of each prism is 60 units³, what would be the height of each prism?
For a volume other than 60 units³, what could be the height of each prism?
Discuss your thinking with your partner. If you disagree, work to reach an agreement.

For access, consult one of our IM Certified Partners.

Select students to share their responses and reasoning. If not brought up in student's explanation, explain that for the last problem, there is more than one possible correct answer. The smallest possible volume that involves all whole number side lengths is \(120 \text{ units}^3\), but there is nothing in the problem that requires all the heights to be whole numbers.

To highlight connections to calculating volume, ask:

“How do you calculate the volume of a prism?” (Display the equation for all to see: \(V = B \boldcdot h\).)
“Since \(V = B \boldcdot h\), how could we find the area of the base if we knew the volume and height of the prism?” (Display the equation for all to see: \(B = V \div h\).)
“If we keep the volume the same, what happens to the height when we increase the area of the base?” (It decreases.)
“If we keep the height the same, what happens to the volume when we increase the area of the base?” (It increases.)

Speaking: MLR8 Discussion Supports. Use this routine to support whole-class discussion. For each response that is shared, ask students to restate and/or revoice what they heard using precise mathematical language. Consider providing students time to restate what they hear to a partner, before selecting one or two students to share with the class. Ask the original speaker if their peer was accurately able to restate their thinking. Call students' attention to any words or phrases that helped to clarify the original statement. This will provide more students with an opportunity to produce language as they interpret the reasoning of others.
Design Principle(s): Support sense-making

Lesson Synthesis

“What information do we need to calculate the volume of a prism?” (Area of the base and the height)
“Explain how you could use layers to find the volume of a prism.” (If you look at the first layer of a prism, you can find how many cubes are in that layer by finding the area of the base. Once you find the number of cubes on the first layer, you multiply that by the number of layers it takes to stack up to the height of the prism.)
“Two prisms have the same base area and height, but different base shapes. Which prism has a greater volume? Explain.” (The two prisms have the same volume. The shape of the base does not matter if it is a prism, only the base area matters.)
“Two clay prisms use the same amount of clay to make them, but the first has a larger height than the second. Which prism has a larger base area?” (The second prism will have a larger base area since a shorter height means a larger base area if the volume is held constant. Imagine squashing the first one down in a nice way to make a shorter, fatter version.)

12.5: Cool-down - Octagonal Box (5 minutes)

For access, consult one of our IM Certified Partners.

Student Lesson Summary

Any cross section of a prism that is parallel to the base will be identical to the base. This means we can slice prisms up to help find their volume. For example, if we have a rectangular prism that is 3 units tall and has a base that is 4 units by 5 units, we can think of this as 3 layers, where each layer has \(4\boldcdot 5\) cubic units.

Two images. First, a prism made of cubes stacked 5 wide, 4 deep, 3 tall. Second, each of the layers of the prism is seperated to show 3 prisms 5 wide, 4 deep, 1 tall.

That means the volume of the original rectangular prism is \(3(4\boldcdot 5)\) cubic units.

This works with any prism! If we have a prism with height 3 cm that has a base of area 20 cm², then the volume is \(3\boldcdot 20\) cm³ regardless of the shape of the base. In general, the volume of a prism with height \(h\) and area \(B\) is

\(\displaystyle V = B \boldcdot h\)

For example, these two prisms both have a volume of 100 cm³.

Two prisms. First prism has a triangular base with area 20 centimeters squared, and height 5 centimeters. Second prism has an irregular base with area 25 centimeters squared, and height 4 centimeters.

Lesson 12

12.1: Three Prisms with the Same Volume (5 minutes)

Warm-up

Launch

Student Facing

Student Response

Activity Synthesis

12.2: Finding Volume with Cubes (10 minutes)

Activity

Launch

Student Facing

Student Response

Launch

Student Facing

Student Response

Activity Synthesis

12.3: Can You Find the Volume? (15 minutes)

Activity

Launch

Student Facing

Student Response

Launch

Student Facing

Student Response

Student Facing

Are you ready for more?

Student Response

Anticipated Misconceptions

Activity Synthesis

12.4: What’s the Prism’s Height? (10 minutes)

Optional activity

Launch

Student Facing

Student Response

Activity Synthesis

Lesson Synthesis

Lesson Synthesis

12.5: Cool-down - Octagonal Box (5 minutes)

Cool-Down

Student Lesson Summary

Student Facing