Lesson 4
Solving for Unknown Angles
Let’s figure out some missing angles.
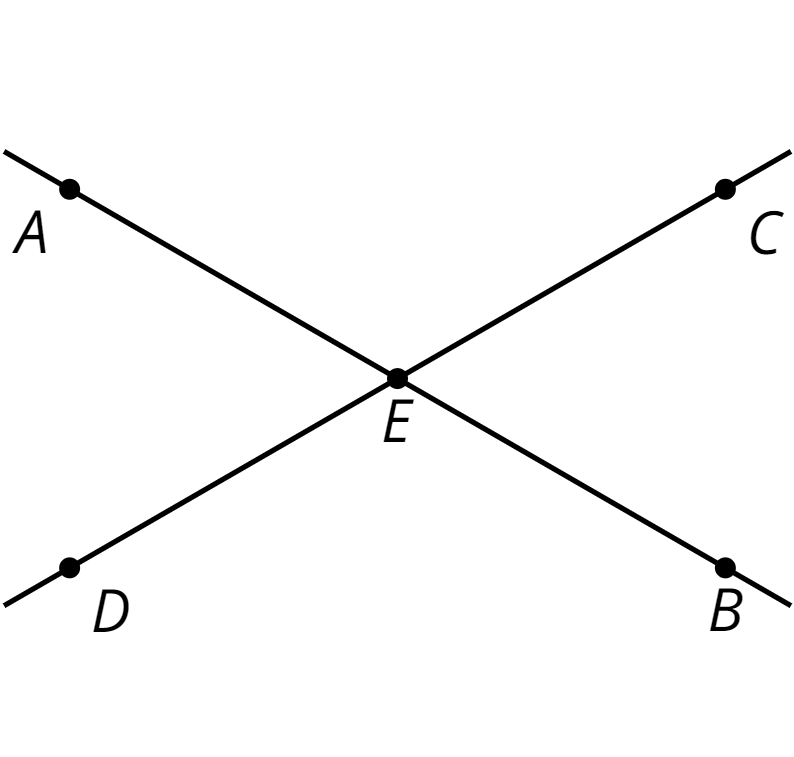
4.1: True or False: Length Relationships
Here are some line segments.

Decide if each of these equations is true or false. Be prepared to explain your reasoning.
\(CD+BC=BD\)
\(AB+BD=CD+AD\)
\(AC-AB=AB\)
\(BD-CD=AC-AB\)
4.2: Info Gap: Angle Finding
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
4.3: What’s the Match?
Match each figure to an equation that represents what is seen in the figure. For each match, explain how you know they are a match.
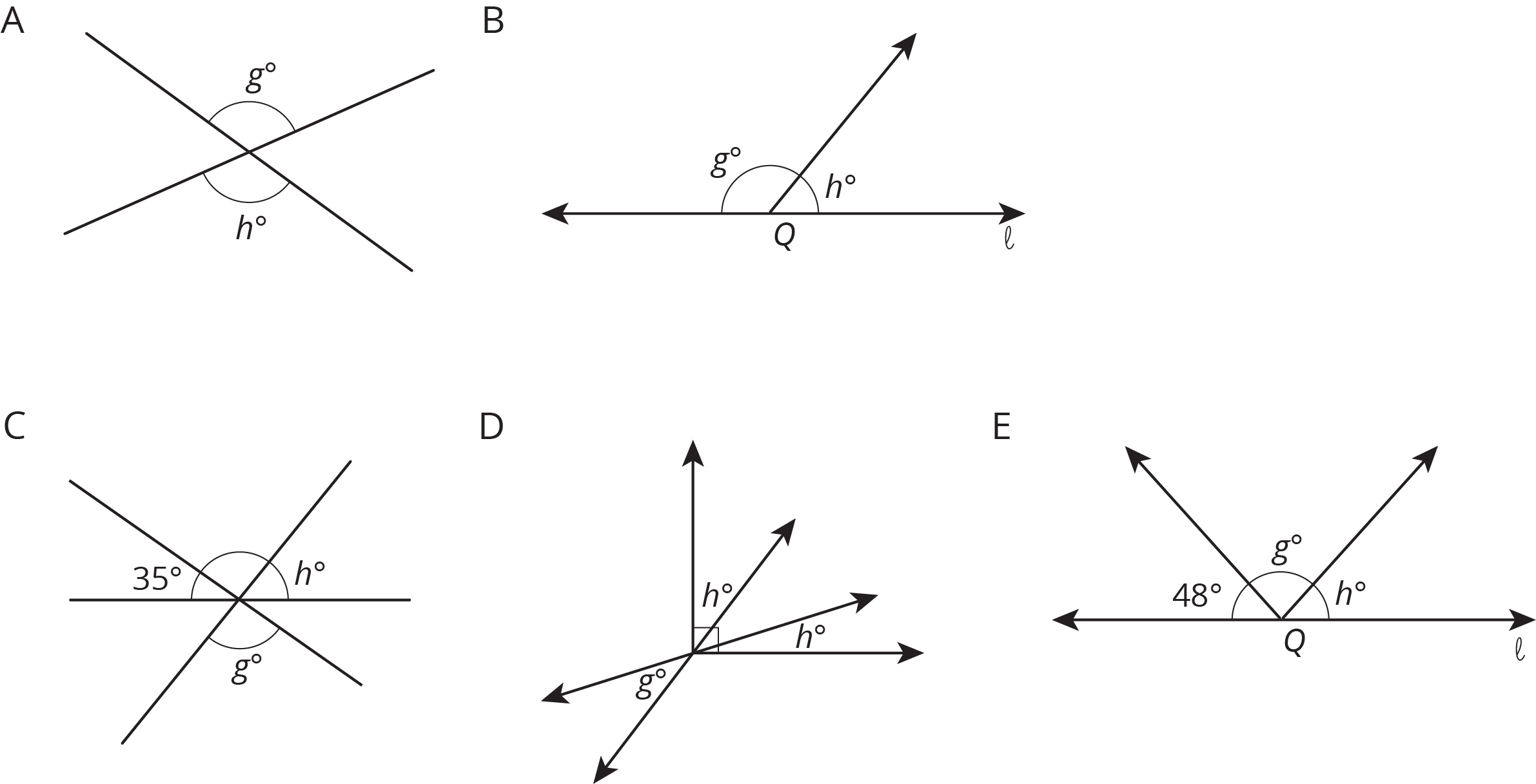
- \(g+h=180\)
- \(g=h\)
- \(2h+g=90\)
- \(g+h+48=180\)
-
\(g+h+35=180\)
- What is the angle between the hour and minute hands of a clock at 3:00?
- You might think that the angle between the hour and minute hands at 2:20 is 60 degrees, but it is not! The hour hand has moved beyond the 2. Calculate the angle between the clock hands at 2:20.
- Find a time where the hour and minute hand are 40 degrees apart. (Assume that the time has a whole number of minutes.) Is there just one answer?
Summary
We can write equations that represent relationships between angles.
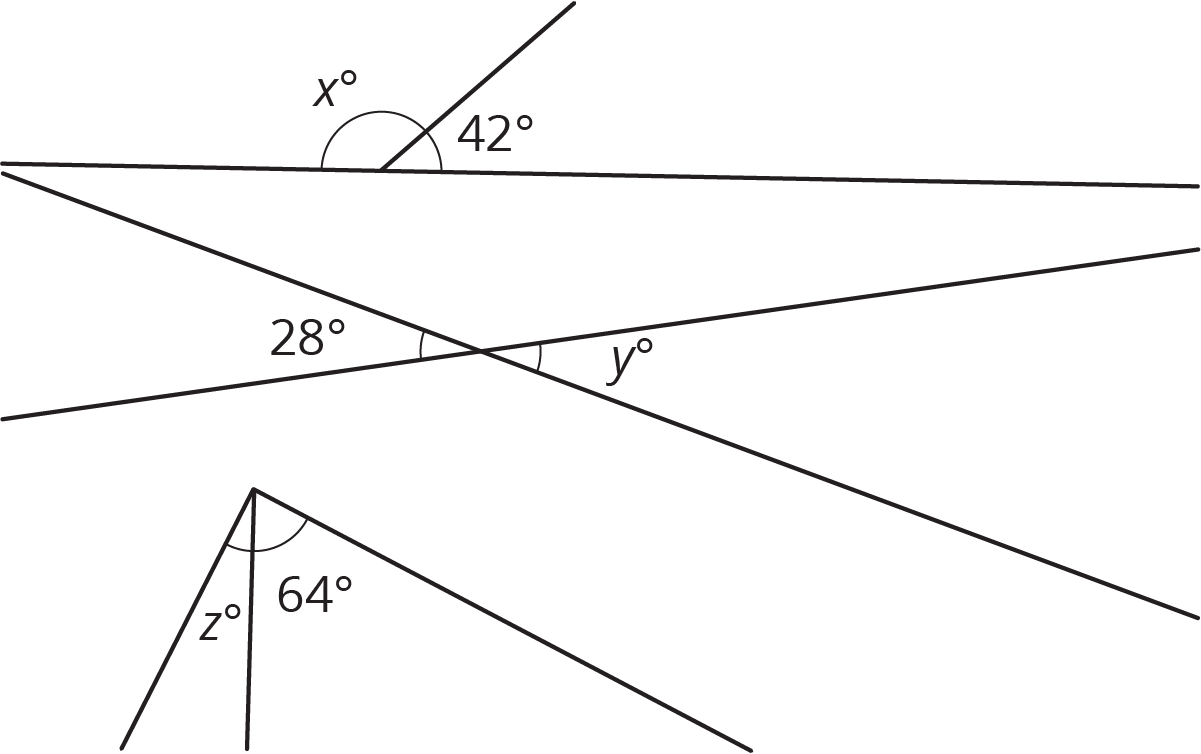
- The first pair of angles are supplementary, so \(x+42 = 180\).
- The second pair of angles are vertical angles, so \(y = 28\).
- Assuming the third pair of angles form a right angle, they are complementary, so \(z + 64 = 90\).
Glossary Entries
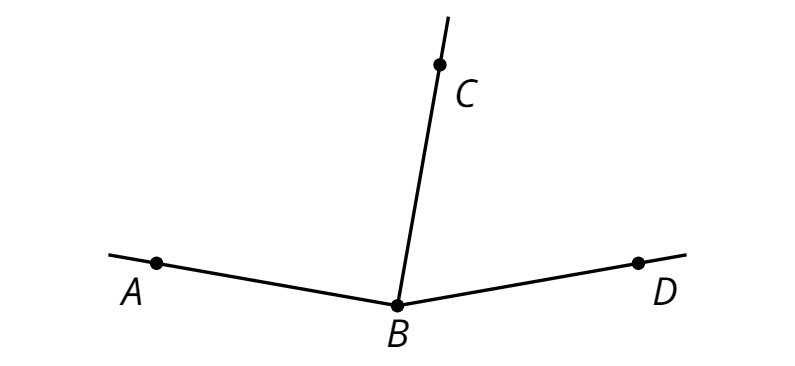
- adjacent angles
Adjacent angles share a side and a vertex.
In this diagram, angle \(ABC\) is adjacent to angle \(DBC\).
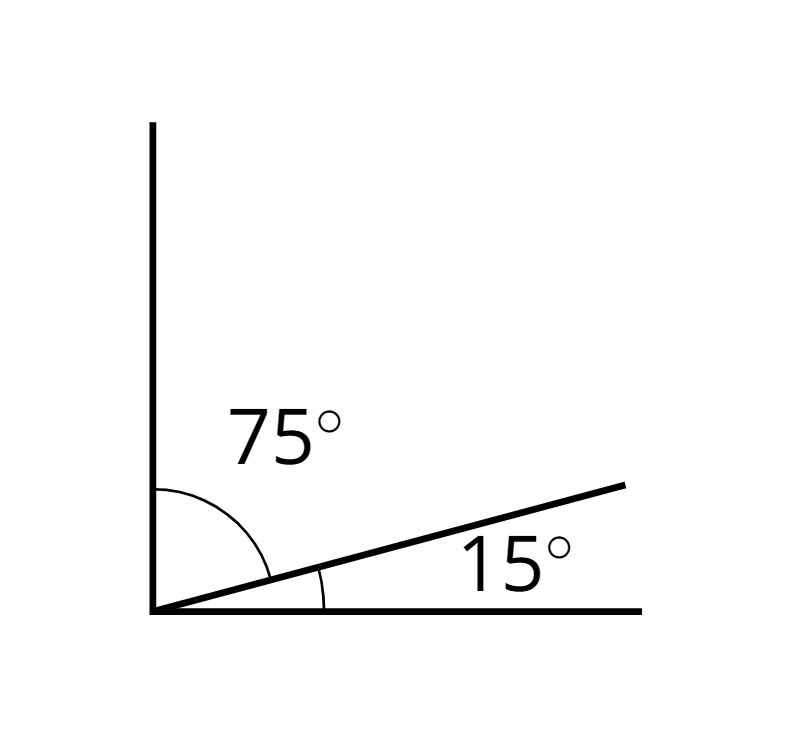
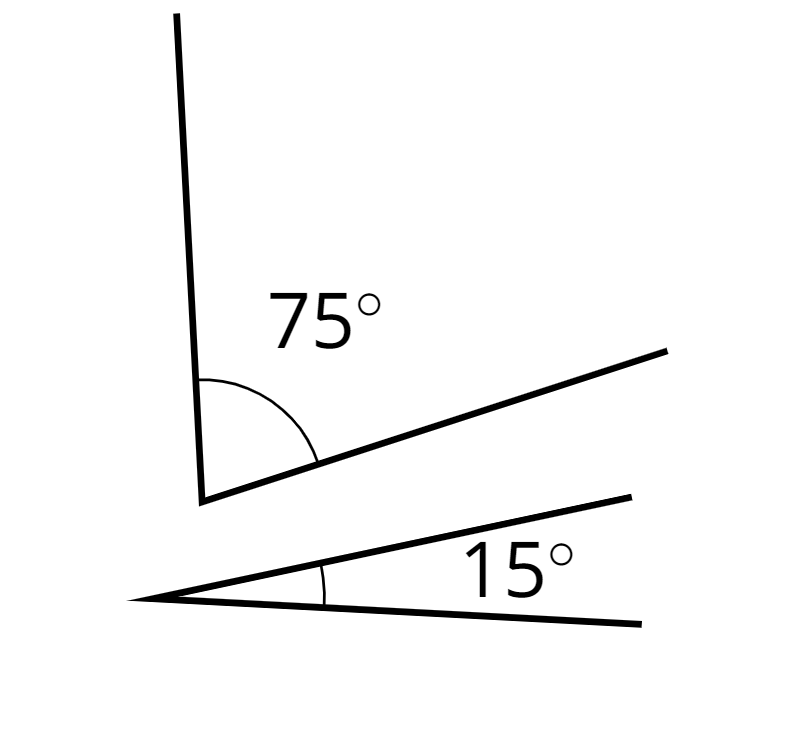
- complementary
Complementary angles have measures that add up to 90 degrees.
For example, a \(15^\circ\) angle and a \(75^\circ\) angle are complementary.
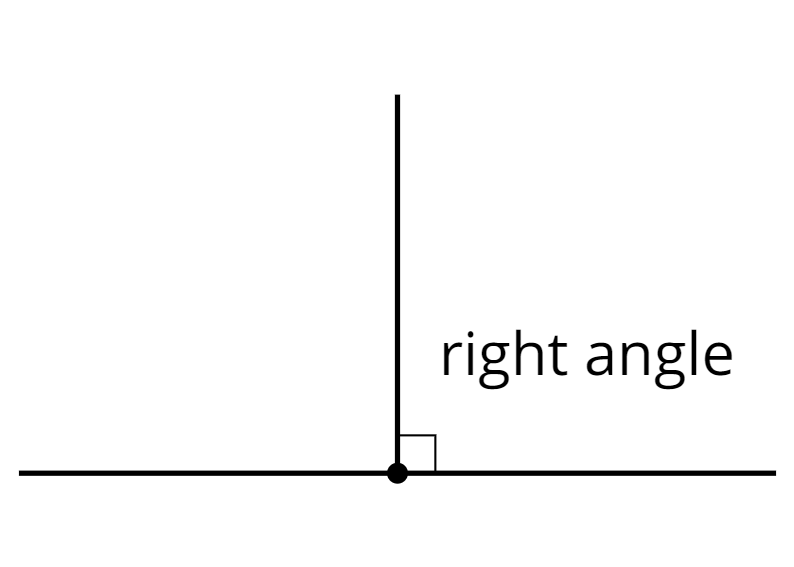
- right angle
A right angle is half of a straight angle. It measures 90 degrees.
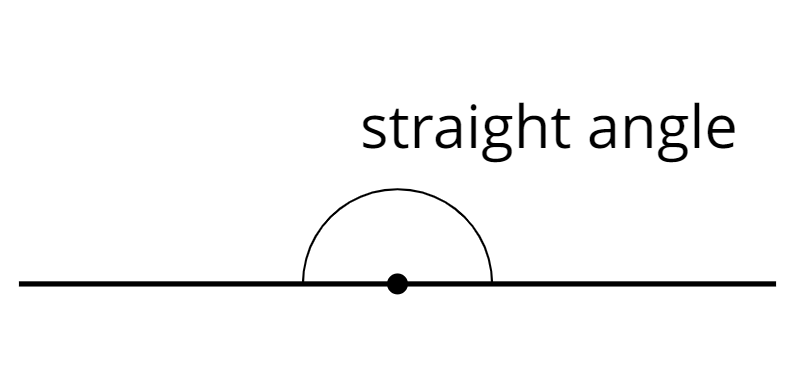
- straight angle
A straight angle is an angle that forms a straight line. It measures 180 degrees.
- supplementary
Supplementary angles have measures that add up to 180 degrees.
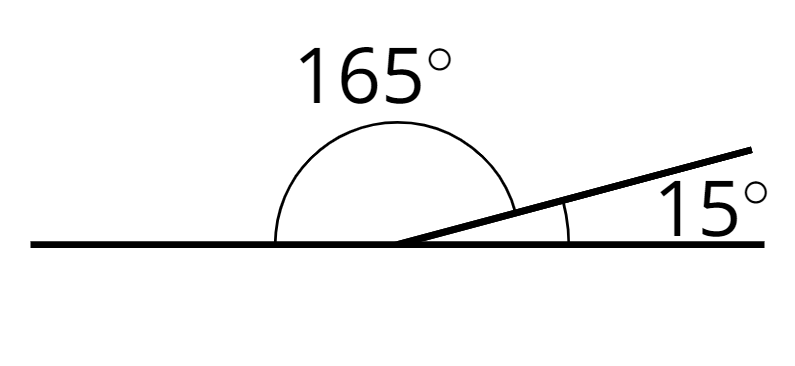
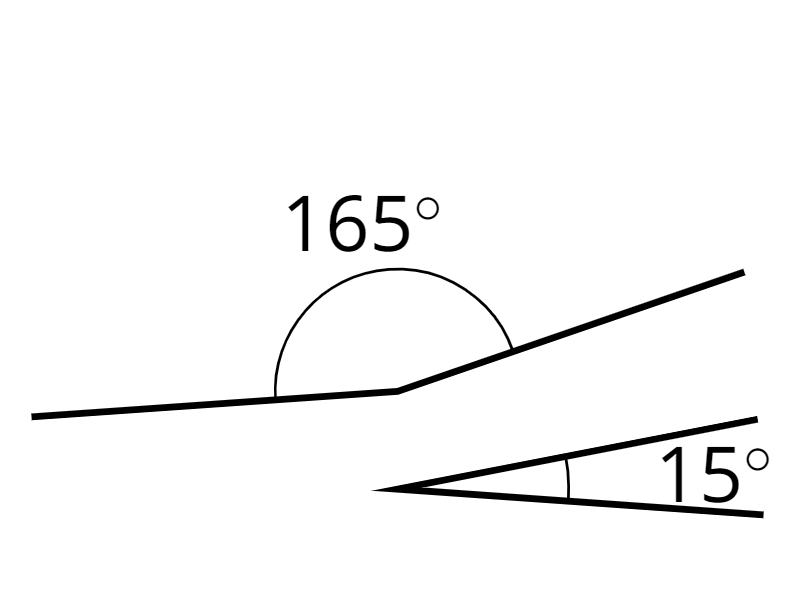
For example, a \(15^\circ\) angle and a \(165^\circ\) angle are supplementary.
- vertical angles
Vertical angles are opposite angles that share the same vertex. They are formed by a pair of intersecting lines. Their angle measures are equal.
For example, angles \(AEC\) and \(DEB\) are vertical angles. If angle \(AEC\) measures \(120^\circ\), then angle \(DEB\) must also measure \(120^\circ\).
Angles \(AED\) and \(BEC\) are another pair of vertical angles.