Lesson 3
Nonadjacent Angles
3.1: Finding Related Statements (5 minutes)
Warm-up
In the previous unit, students worked extensively with writing equations in equivalent forms, for example, rewriting \(2x+50=7\) as \(2x=7-50\). A new wrinkle here is that each equation has two variables. Equations with more than one variable will be studied extensively in grade 8, but here we are using the concrete context of geometry to help make sense of it.
The purpose of this warm-up is for students to use structure to reason about equivalent equations. In this unit, students will write equations to represent how angles are related to each other, and this warm-up helps prepare for that work.
All of the given statements could be true so students may be quick to say each of them must be true. Ask these students if there is a case when that particular statement would not be true for possible values for \(a\) and \(b\). As students discuss their responses with a partner, monitor for students who correctly answered each question to share during the whole-class discussion.
Launch
Arrange students in groups of 2.
Ask students, “If we know for sure that \(a+b=180\), what are some possible values of \(a\) and \(b\)?” Give students 30 seconds of quiet think time, and then ask several students to share their responses. Some examples are \(a=90\) and \(b=90\), \(a=0\) and \(b=180\), and \(a=10\) and \(b=170\). Tell students that in this activity, we know for sure that \(a+b=180\), but we don’t know the exact values of \(a\) and \(b\).
Give students 2 minutes of quiet work time followed by 1 minute to discuss their responses with a partner. Follow with a whole-class discussion.
Student Facing
Given \(a\) and \(b\) are numbers, and \(a+b=180\), which statements also must be true?
\(a=180-b\)
\(a-180=b\)
\(360=2a+2b\)
\(a=90\) and \(b=90\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may assume \(a\) and \(b\) both have a value of 90. Explain that this may be true, but that it is also possible that \(a\) and \(b\) are not equal to each other.
Activity Synthesis
Select previously identified students to explain their reasoning for each statement. Poll the class if they agree or disagree after each student shares. If students disagree, allow students to discuss until they come to an agreement. Consider asking some of the following questions while students discuss:
- “Do you have an example that might support this statement being true (or untrue)?”
- “What evidence do you have to support that statement being true (or untrue)?”
- “What other values of \(a\) and \(b\) might work?”
- “What was done to the equation to make the statement true (or untrue)?”
If any of the answers the students decide upon are incorrect, give an example of when the statement would not be true.
3.2: Polygon Angles (10 minutes)
Activity
In this activity, students see that angles do not need to be adjacent to each other in order to be considered complementary or supplementary. Students are given two different polygons and are asked to find complementary and supplementary angles, using any tools in their geometry toolkit. The most likely approaches are:
- measure each angle with a protractor and and look for any that sum to 180 or 90 degrees.
- trace the legs of an angle with tracing paper and align its vertex and one leg with another angle to see if the two angles, when adjacent, form a straight angle or a right angle.
As students work, monitor for students who use either approach listed or some other strategy. Also, encourage students to use precise vocabulary and language that they learned in previous activities and lessons (MP6).
Launch
Remind students that in the previous lesson they learned the meaning of complementary and supplementary when describing angles. Invite students to share their definitions of the words and consider displaying the meanings for all to see through the remainder of the class. If students include in their definitions the idea that the angles need to be adjacent (for example, that they “make a straight line” or “make a right angle”), point out that while that was true for all the examples they have seen so far, that was not a part of the definition. Explain that angles do not need to be adjacent to one another to be complementary or supplementary. They just have to sum to 90 or 180 degrees.
Keep students in the same groups. Provide access to geometry toolkits. Give students 3–4 minutes of quiet work time, followed by partner and whole-class discussions.
Supports accessibility for: Language; Organization
Student Facing
Use any useful tools in the geometry toolkit to identify any pairs of angles in these figures that are complementary or supplementary.

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may struggle to use a protractor to measure angles when the rays are not drawn long enough to reach the edge of the protractor. Prompt them to extend the sides of the angle using a straightedge.
Activity Synthesis
Select previously identified students to share their answers and reasoning. If possible, have a student demonstrate each method for finding pairs of angles: measuring with a protractor or using tracing paper. Ensure that correct use of a protractor to find the measure of an angle is clearly and carefully demonstrated. This will help all students prepare for the next activity where everyone will be using a protractor.
Design Principle(s): Support sense-making
3.3: Vertical Angles (15 minutes)
Activity
The purpose of this activity is for students to learn about vertical angles. Each student draws two intersecting lines and measures the four resulting angles. Then, students examine multiple examples to come up with a conjecture for any relationships they noticed (MP8). Because of the focus of the previous activity, students will likely notice that there are adjacent supplementary angles in their drawings. Encourage them to look for any other patterns they can find.
Launch
Arrange students in groups of 2–4. Provide access to geometry toolkits.
Ask students to read the task statement quietly to themselves. Then, ask them to read it again and underline any words that they are uncertain about. Invite students to share any words they underlined and record them for all to see. Before students start working, explain the meaning of any word they identified, which may include:
- intersecting—Some students may think that “intersecting” means “perpendicular.” In this activity, it is important for students to examine some examples of vertical angles made by intersecting lines that are not perpendicular. Consider holding up two meter sticks to demonstrate several examples of two lines that intersect versus two lines that do not intersect. Clarify that intersecting lines do not have to be perpendicular.
- conjecture—Explain that a conjecture is a statement we think is true but aren’t certain about. It is more than just a guess. A conjecture could be a guess that is based on some evidence.
Give students 2–3 minutes to draw and measure the figure. Remind them to draw arcs to label the degree measures of their angles. Follow with small-group and whole-class discussions.
Supports accessibility for: Conceptual processing; Memory
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Use a straightedge to draw two intersecting lines. Use a protractor to measure all four angles whose vertex is located at the intersection.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may label the angle measures toward the end of the rays, where they read the number from the protractor. This is not precise enough, because two different angles share each ray. Remind students about drawing arcs to clarify which angle they measured.
Activity Synthesis
The goal of this discussion is for students to see that two intersecting lines form vertical angles, and the angles across from each other are congruent. Select students to share their conjectures. If there are students who can use supplementary angles to explain why vertical angles have equal measures, put them last in the sequence.
Define vertical angles as a pair of angles, formed by two intersecting lines, that are opposite each other.
Display the image and ask students to identify four pairs of vertical angles. In particular, students may have trouble seeing that angles \(FJI\) and \(HJG\) are vertical angles.
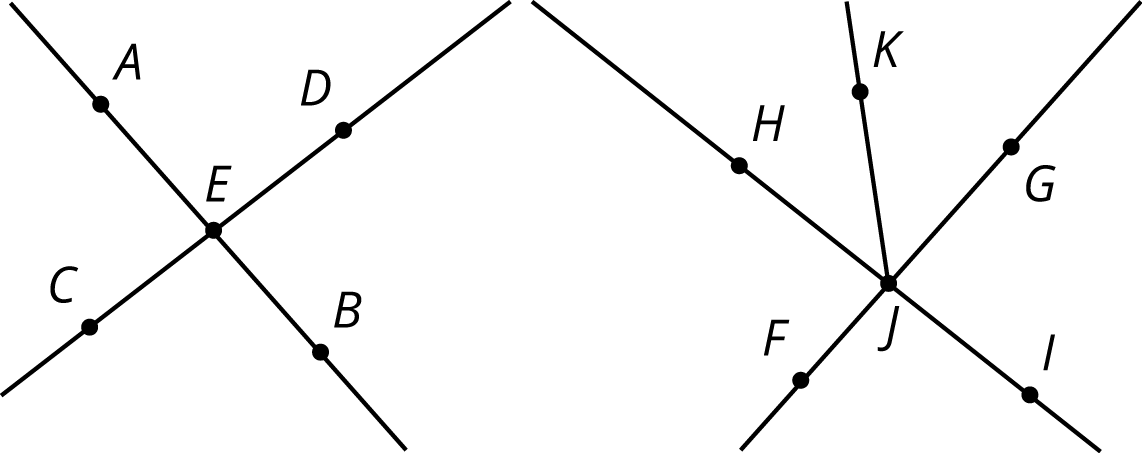
Although students don’t need to know a proof that vertical angles always have the same measure, it may be helpful to show one way to understand why they are. In the image. . .
- Angles \(AED\) and \(AEC\) are supplementary, so the sum of their measures is 180 degrees.
- Angles \(AEC\) and \(CEB\) are also supplementary, so the sum of their measures is also 180 degrees.
- If we take angle \(AEC\) away from the straight angles, we see that angles \(AED\) and \(CEB\) must have the same measure.
3.4: Row Game: Angles (10 minutes)
Optional activity
This activity gives students an opportunity to practice recognizing complementary, supplementary, and vertical angles and using what they know about those types of angles to find unknown angle measures. Some students may feel comfortable writing equations to show their reasoning, but it is not important that all students use this strategy at this point, as it will be the focus of future lessons. Encourage students to continue using the new vocabulary.
Launch
Arrange students in groups of 2. Make sure students know how to play a row game. Give students 5–6 minutes of partner work time followed by a whole-class discussion.
Student Facing
Find the measure of the angles in one column. Your partner will work on the other column. Check in with your partner after you finish each row. Your answers in each row should be the same. If your answers aren’t the same, work together to find the error and correct it.
column A
column B
\(P\) is on line \(m\). Find the value of \(a\).
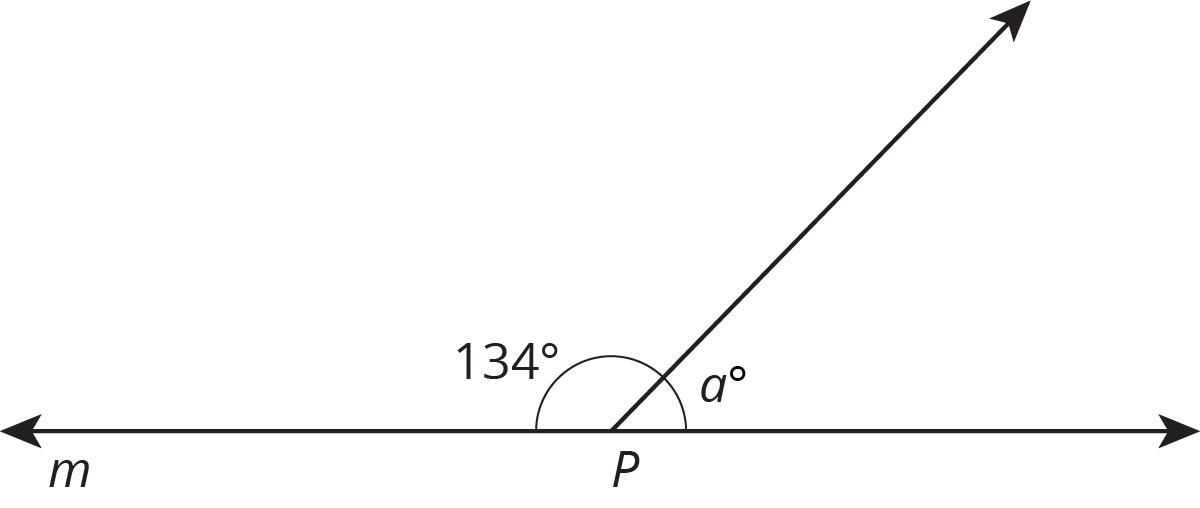
Find the value of \(b\).
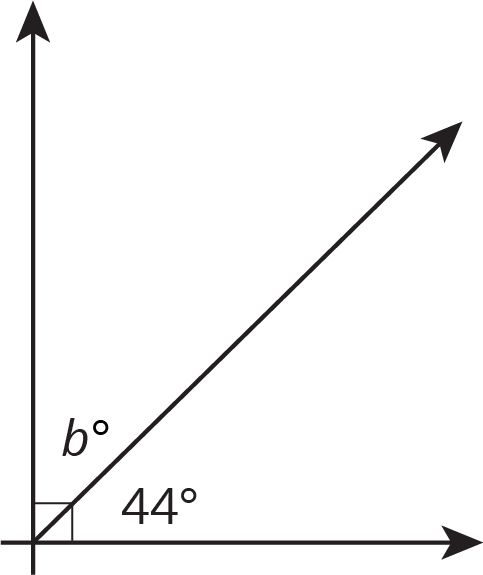
Find the value of \(a\).
In right triangle \(LMN\), angles \(L\) and \(M\) are complementary. Find the measure of angle \(L\).
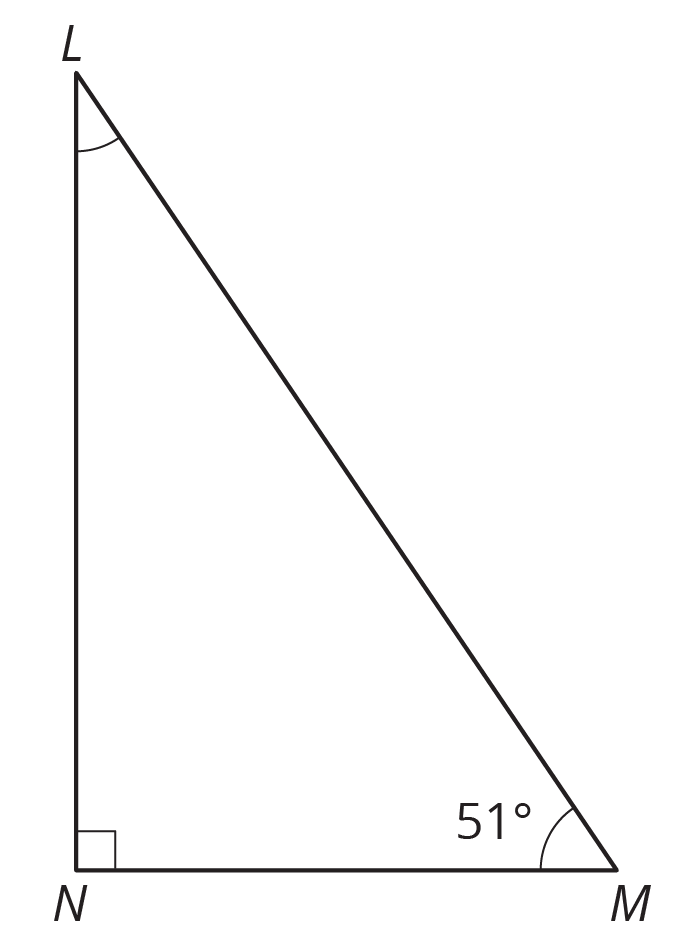
column A
column B
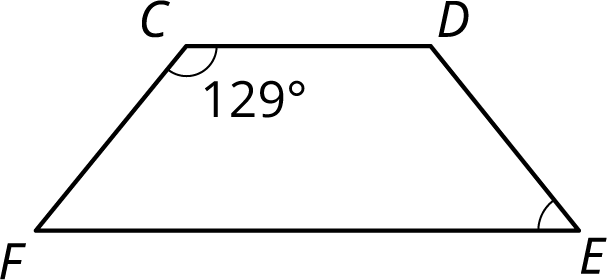
Angle \(C\) and angle \(E\) are supplementary. Find the measure of angle \(E\).
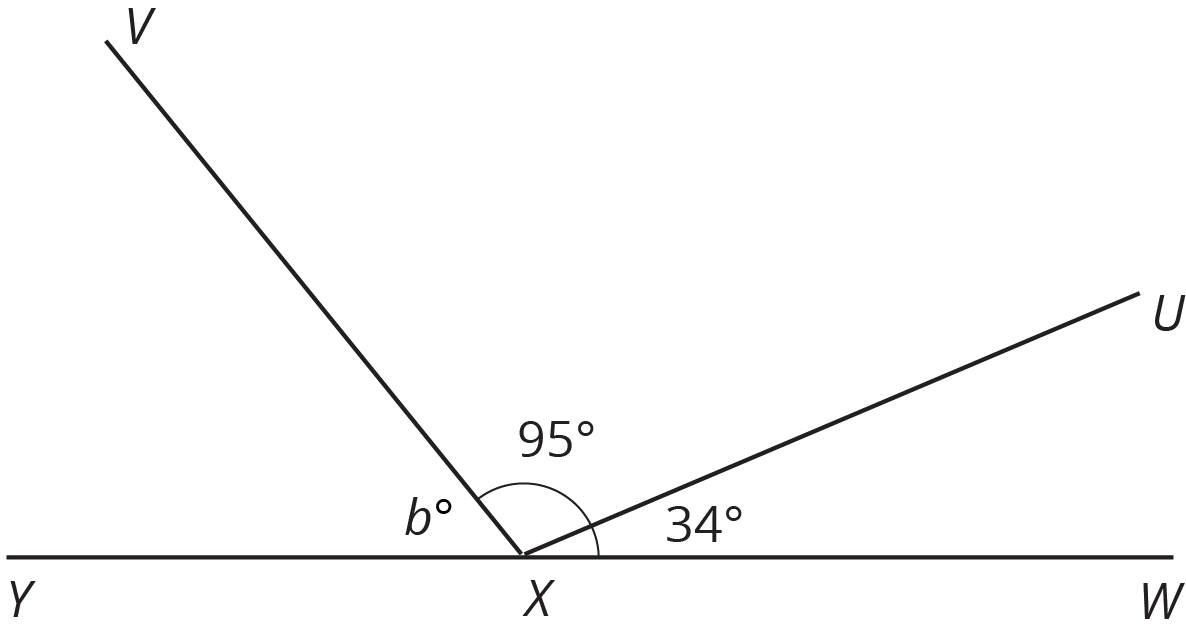
\(X\) is on line \(WY\). Find the value of \(b\).
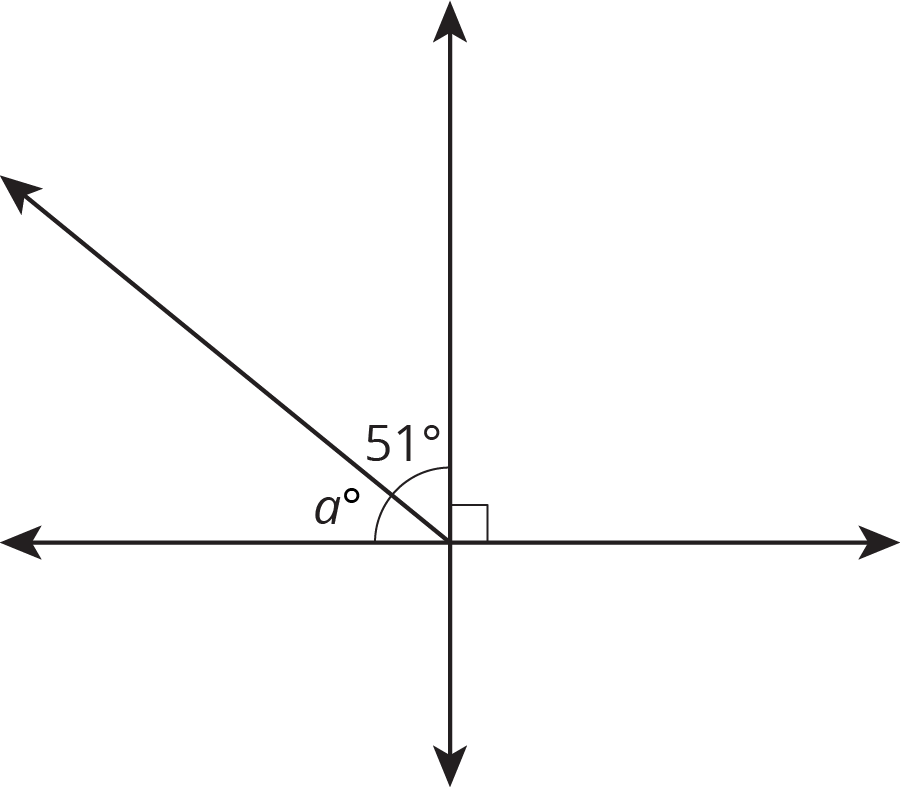
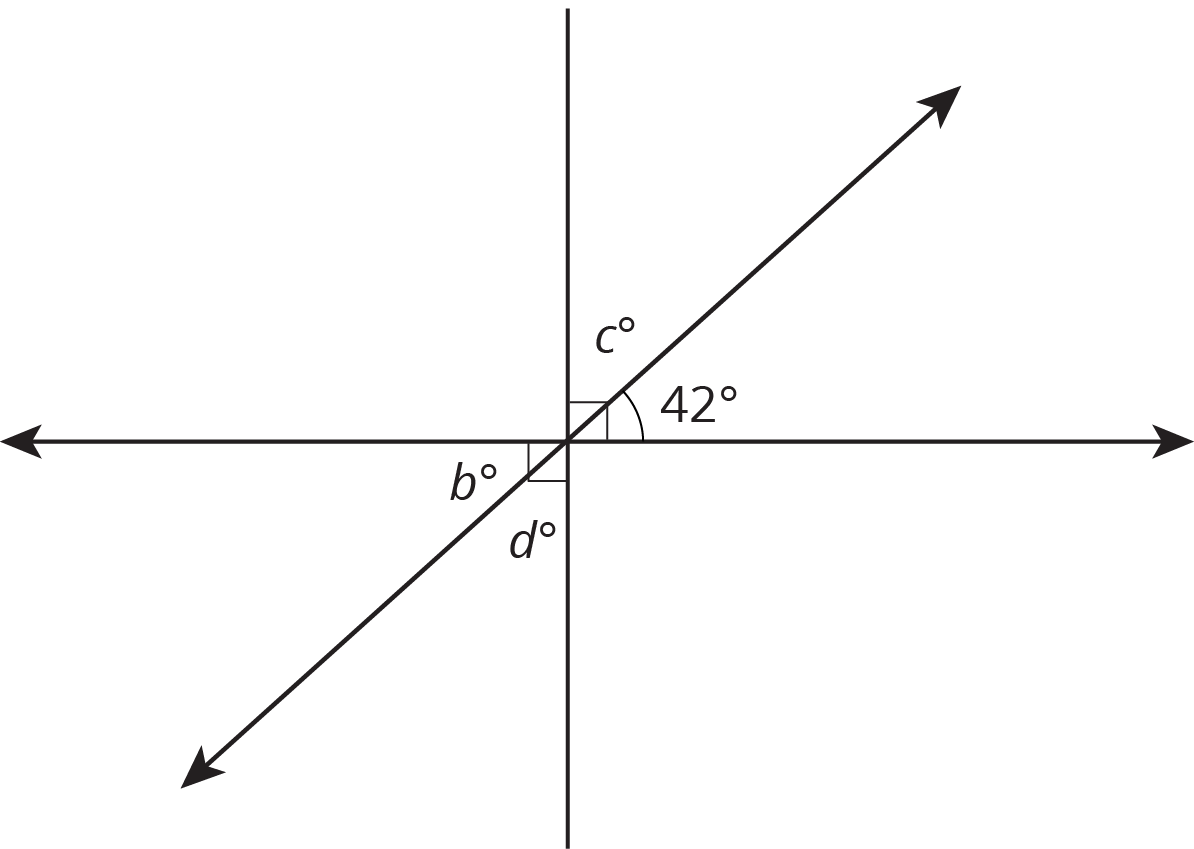
Find the value of \(c\).
\(B\) is on line \(FW\). Find the measure of angle \(CBW\).
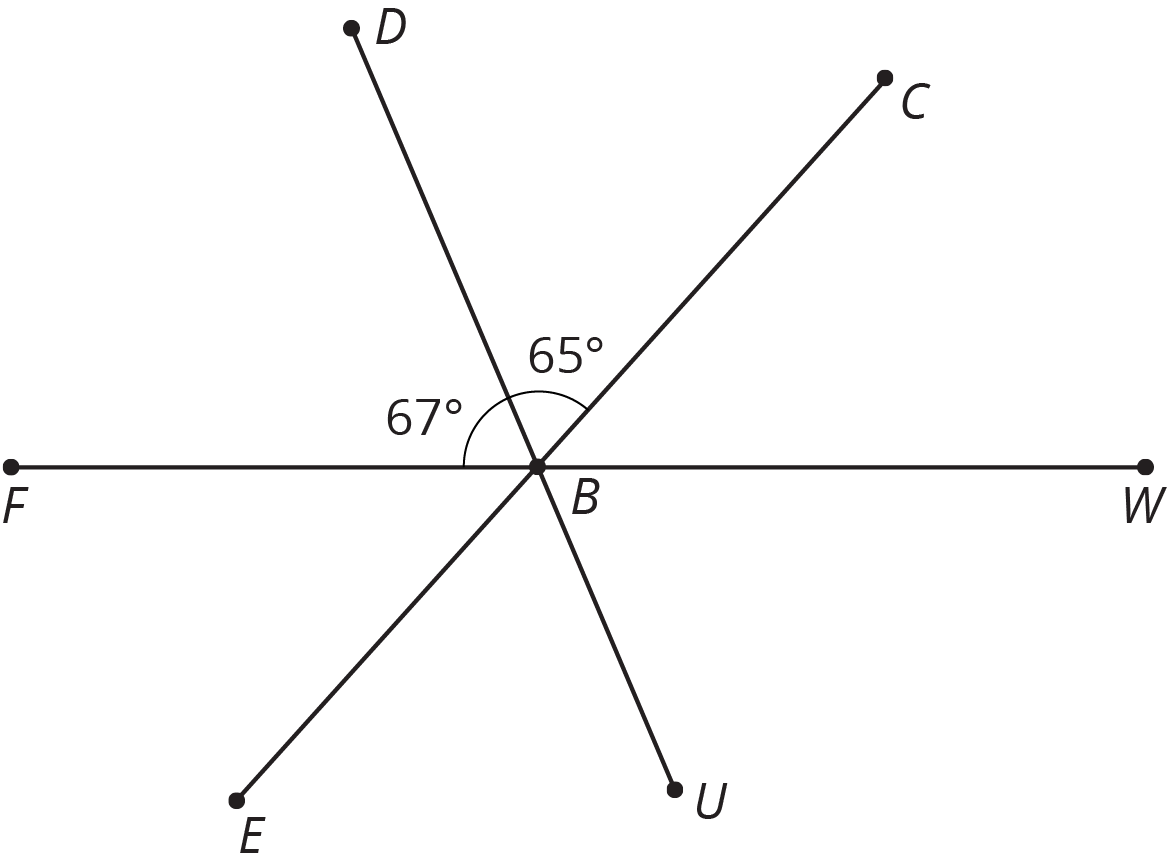
Two angles are complementary. One angle measures 37 degrees. Find the measure of the other angle.
Two angles are supplementary. One angle measures 127 degrees. Find the measure of the other angle.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to see relationships of angles in figures, prompt students to look for complementary, supplementary, or vertical angles.
Activity Synthesis
Ask students, “Were there any rows that you and your partner did not get the same answer?” Invite students to share how they came to an agreement on the final answer for the problems in those rows.
Consider asking some of the following questions:
- “Did you and your partner use the same strategy for each row?”
- “What was the same and different about both of your strategies?”
- “Did you learn a new strategy from your partner?”
- “Did you try a new strategy while working on these questions?”
Design Principle(s): Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
- Do supplementary or complementary angles need to be next to one another? (No.) Think of examples where they are not.
- What are vertical angles? (A pair of angles across from one another where two lines cross.)
- What is true about the measures of vertical angles? (The measures are always the same.)
Display diagrams and definitions of new vocabulary somewhere in the classroom so that students can refer back to them during subsequent lessons. “Vertical angles” is new vocabulary; you might consider also adding “intersecting lines” and “conjecture.” As the unit progresses, new terms can be added.
3.5: Cool-down - Finding Angle Pairs (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When two lines cross, they form two pairs of vertical angles. Vertical angles are across the intersection point from each other.
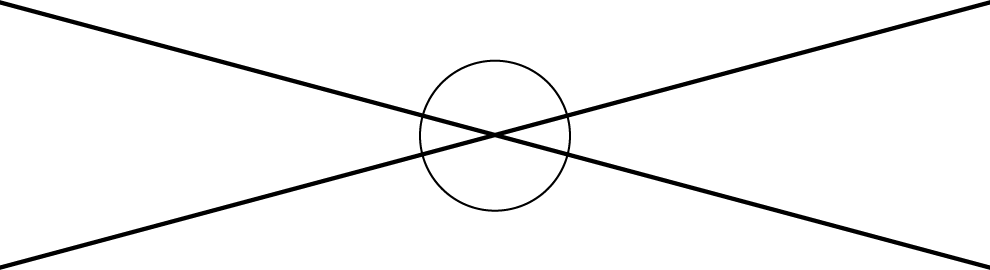
Vertical angles always have equal measure. We can see this because they are always supplementary with the same angle. For example:

This is always true!

\(a+b = 180\) so \(a = 180-b\).
\(c+b = 180\) so \(c = 180-b\).
That means \(a = c\).