Lesson 10
Drawing Triangles (Part 2)
10.1: Using a Compass to Estimate Length (5 minutes)
Warm-up
The purpose of this warm-up is to remind students that a compass is useful for transferring a length in general, and not just for drawing circles. As students discuss answers with their partners, monitor for students who can clearly explain how they can use the compass to compare the length of the third side.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet work time followed by time to discuss their answers with their partner. Follow with a whole-class discussion. Provide access to geometry toolkits and compasses.
Student Facing
- Draw a \(40^\circ\) angle.
- Use a compass to make sure both sides of your angle have a length of 5 centimeters.
-
If you connect the ends of the sides you drew to make a triangle, is the third side longer or shorter than 5 centimeters? How can you use a compass to explain your answer?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask previously identified students to share their responses to the final question. Display their drawing of the angle for all to see. If not mentioned in students’ explanations, demonstrate for all to see how to use the compass to estimate the length of the third side of the triangle.
10.2: Revisiting How Many Can You Draw? (15 minutes)
Activity
Students continue to practice drawing triangles from given conditions and categorizing their results. This activity focuses on the inclusion of a single angle and two sides. Again, they do not need to memorize which conditions result in unique triangles, but should begin to notice how some conditions (such as the equal side lengths) result in certain requirements for the completed triangle.
There is an optional blackline master that can help students organize their work at trying different configurations of the first set of measurements. If you provide students with a copy of the blackline master, ask them to determine whether any of the configurations result in the same triangle, as well as whether any one configuration results in two possible triangles.
Launch
Keep students in same groups. Remind students of the activity in a previous lesson where they used the strips and fasteners to draw triangles on their paper. Ask what other tool also helps you find all the points that are a certain distance from a center point (a compass). Distribute optional blackline masters if desired. Provide access to geometry toolkits and compasses.
Give students 7–8 minutes of partner work time, followed by a whole-class discussion.
If students have access to digital activities there is an applet that allows for triangle construction.
Design Principle(s): Maximize meta-awareness; Cultivate conversation
Student Facing
Use the applet to draw triangles.
-
Draw as many different triangles as you can with each of these sets of measurements:
- One angle measures \(40^\circ\), one side measures 4 cm and one side measures 5 cm.
- Two sides measure 6 cm and one angle measures \(100^\circ\).
-
Did either of these sets of measurements determine one unique triangle? How do you know?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Keep students in same groups. Remind students of the activity in a previous lesson where they used the strips and fasteners to draw triangles on their paper. Ask what other tool also helps you find all the points that are a certain distance from a center point (a compass). Distribute optional blackline masters if desired. Provide access to geometry toolkits and compasses.
Give students 7–8 minutes of partner work time, followed by a whole-class discussion.
If students have access to digital activities there is an applet that allows for triangle construction.
Design Principle(s): Maximize meta-awareness; Cultivate conversation
Student Facing
-
Draw as many different triangles as you can with each of these sets of measurements:
-
One angle measures \(40^\circ\), one side measures 4 cm, and one side measures 5 cm.
-
Two sides measure 6 cm, and one angle measures \(100^\circ\).
-
-
Did either of these sets of measurements determine one unique triangle? How do you know?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may draw two different orientations of the same triangle for the first set of conditions, with the \(40^\circ\) angle in between the 4 cm and 5 cm sides. Prompt them to use tracing paper to check whether their two triangles are really different (not identical copies).
If students struggle to create more than one triangle from the first set of conditions, prompt them to write down the order they already used for their measurements and then brainstorm other possible orders they could use.
Activity Synthesis
Ask one or more students to share how many different triangles they were able to draw with each set of conditions. Select students to share their solutions.
If not brought up in student explanations, point out that for the first problem, one possible order for the measurements (\(40^\circ\), 5 cm, 4 cm) can result in two different triangles (the bottom two in the solution image). One way to show this is to draw a 5 cm segment and then use a compass to draw a circle with a 4 cm radius centered on the segment’s left endpoint. Next, draw a ray at a \(40^\circ\) angle centered on the segment’s right endpoint. Notice that this ray intersects the circle twice. Each one of these points could be the third vertex of the triangle. While it is helpful for students to notice this interesting aspect of their drawing, it is not important for students to learn rules about the number of possible triangles given different sets of conditions.
If the optional blackline master was used, ask students:
- “Which configurations made identical triangles?” (the top left and bottom left)
- “Which configurations made more than one triangle?” (the bottom right)
If not mentioned by students, explain to students that the top left and bottom left configurations result in the same triangle, because in both cases the \(40^\circ\) angle is in between the 4 cm and 5 cm sides and that the bottom right configuration results in two different triangles, because the arc intersects the ray in two different places.
MLR 1 (Stronger and Clearer Each Time): Before discussing the second set of conditions as a whole class, have student pairs share their reasoning for why there were no more triangles that could be drawn with the given measures, with two different partners in a row. Have students practice using mathematical language to be as clear as possible when sharing with the class, when and if they are called upon.
Supports accessibility for: Attention; Social-emotional skills
10.3: Three Angles (15 minutes)
Activity
This activity focuses on including three angle conditions. The goal is for students to notice that some angle conditions result in a large number of possible triangles (all scaled copies of one another) or are impossible to create. Students are not expected to learn that the angles must sum to 180 degrees in a triangle, but are not barred from noticing this fact.
Launch
Arrange students in groups of 2. Tell students that they should attempt to create a triangle with the given specifications. If they can create one, they should attempt to either create at least one more or justify to themselves why there is only one. If they cannot create any, they should show some valid attempts to include as many pieces as they can and be ready to explain why they cannot include the remaining conditions.
Give students 5 minutes of quiet work time followed by time to discuss the triangles they could make with a partner. Follow with a whole-class discussion. Provide access to geometry toolkits and compasses.
If using the digital lesson, students should still try to create a triangle with the given specifications. If they can create one, they should attempt to either create at least one more or justify to themselves why there is only one. If they cannot create any, they should be ready to explain some of their attempts and why they cannot include the remaining conditions.
Student Facing
Use the applet to draw triangles. Sides can overlap.
- Draw as many different triangles as you can with each of these sets of measurements:
- One angle measures \(50^\circ\), one measures \(60^\circ\), and one measures \(70^\circ\).
- One angle measures \(50^\circ\), one measures \(60^\circ\), and one measures \(100^\circ\).
- Did either of these sets of measurements determine one unique triangle? How do you know?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Using only the point, segment, and compass tools provided, create an equilateral triangle. You are only successful if the triangle remains equilateral while dragging its vertices around.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Tell students that they should attempt to create a triangle with the given specifications. If they can create one, they should attempt to either create at least one more or justify to themselves why there is only one. If they cannot create any, they should show some valid attempts to include as many pieces as they can and be ready to explain why they cannot include the remaining conditions.
Give students 5 minutes of quiet work time followed by time to discuss the triangles they could make with a partner. Follow with a whole-class discussion. Provide access to geometry toolkits and compasses.
If using the digital lesson, students should still try to create a triangle with the given specifications. If they can create one, they should attempt to either create at least one more or justify to themselves why there is only one. If they cannot create any, they should be ready to explain some of their attempts and why they cannot include the remaining conditions.
Student Facing
-
Draw as many different triangles as you can with each of these sets of measurements:
-
One angle measures \(50^\circ\), one measures \(60^\circ\), and one measures \(70^\circ\).
-
One angle measures \(50^\circ\), one measures \(60^\circ\), and one measures \(100^\circ\).
-
-
Did either of these sets of measurements determine one unique triangle? How do you know?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Using only a compass and the edge of a blank index card, draw a perfectly equilateral triangle. (Note! The tools are part of the challenge! You may not use a protractor! You may not use a ruler!)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to get started, remind them of Lin’s technique of using the protractor and a ruler to make an angle that can move along a line.
Activity Synthesis
Select students to share their drawings and display them for all to see. Ask students:
- “Were there any sets of measurements that produced a unique triangle?” (no)
- “Which combinations of angles could not be drawn?” (the angles in the second problem, \(50^\circ, 60^\circ, 100^\circ\))
- “Why is there more than one triangle that can be made with the measurements in the first problem?” (because there are no side lengths mentioned, so we can create scaled copies of the triangles with the same angles but with shorter or longer side lengths)
MLR 1 (Stronger and Clearer Each Time): Before discussing the second set of conditions as a whole class, have student pairs share their reasoning for why there were no triangles that could be drawn with the given measures, with two different partners in a row. Have students practice using mathematical language to be as clear as possible when sharing with the class, when and if they are called upon.
Lesson Synthesis
Lesson Synthesis
- How was a compass useful in drawing triangles today? (It helps find all the points a certain distance away.)
- What strategies did you use to include two given side lengths and a given angle? (Draw one of the side lengths and use a protractor to draw the angle at one end, then use a compass to finish the picture.)
- What strategies did you use to include three given angles? (Draw one angle then use a protractor and ruler to slide along one side of the first angle.)
10.4: Cool-down - Finishing Noah’s Triangle (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A triangle has six measures: three side lengths and three angle measures.
If we are given three measures, then sometimes, there is no triangle that can be made. For example, there is no triangle with side lengths 1, 2, 5, and there is no triangle with all three angles measuring \(150^\circ\).

Sometimes, only one triangle can be made. By this we mean that any triangle we make will be the same, having the same six measures. For example, if a triangle can be made with three given side lengths, then the corresponding angles will have the same measures. Another example is shown here: an angle measuring \(45^\circ\) between two side lengths of 6 and 8 units. With this information, one unique triangle can be made.
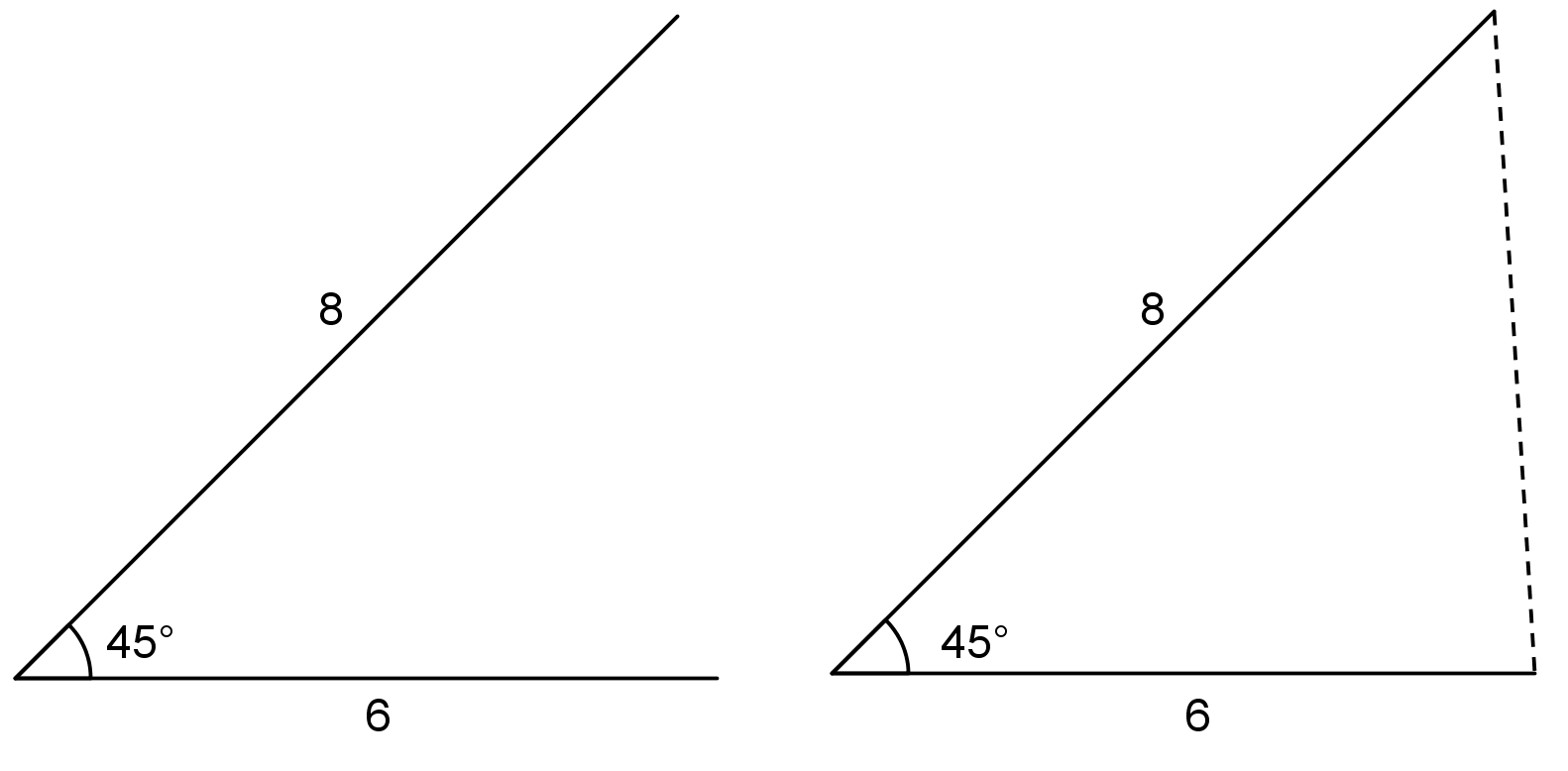
Sometimes, two or more different triangles can be made with three given measures. For example, here are two different triangles that can be made with an angle measuring \(45^\circ\) and side lengths 6 and 8. Notice the angle is not between the given sides.
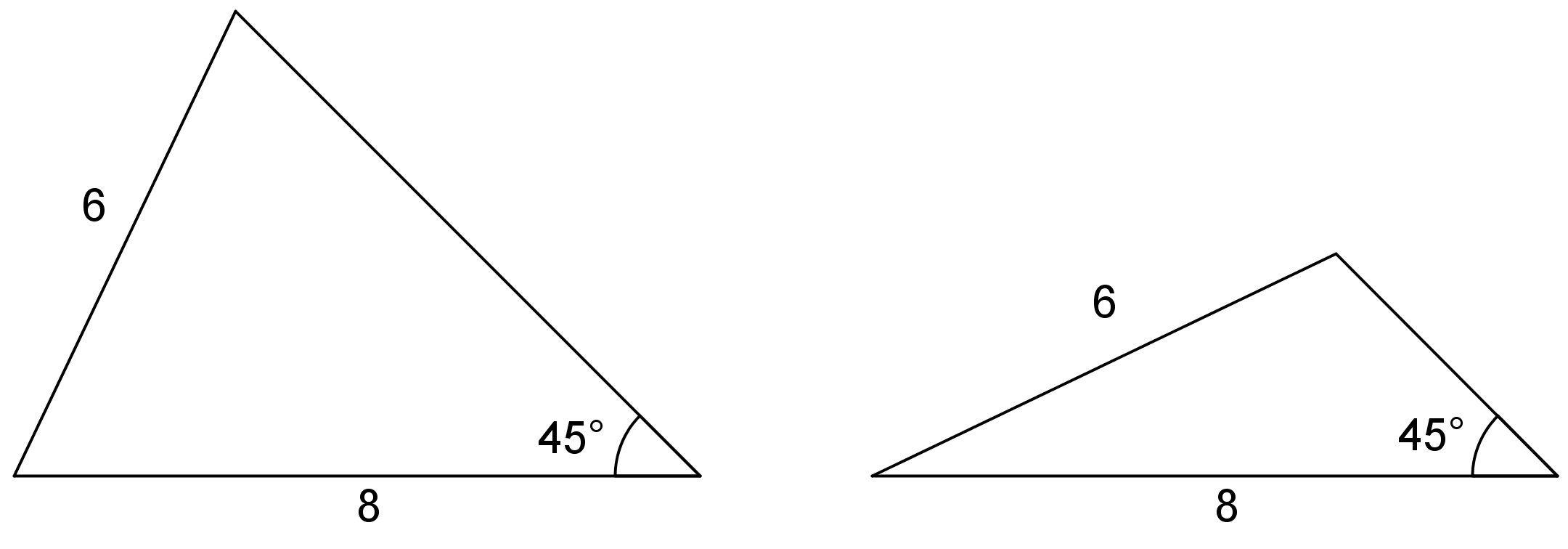
Three pieces of information about a triangle’s side lengths and angle measures may determine no triangles, one unique triangle, or more than one triangle. It depends on the information.