Lesson 7
Building Polygons (Part 2)
7.1: Where Is Lin? (5 minutes)
Warm-up
The purpose of this warm-up is to remind students that when you have a fixed starting point, all the possible endpoints for a segment of a given length form a circle (centered around the starting point). The context of finding Lin’s position in the playground helps make the geometric relationships more concrete for students. Since there are many possible distances between Lin and the swings (but not infinitely many), this activity serves as an introduction to formalizing rules about what lengths can and cannot be used to form a triangle.
Monitor for students who come up with different locations for Lin, as well as students who recognize that there are many possible locations, to share during the whole-class discussion.
Launch
Arrange students in groups of 2. If necessary, remind students of the directions north, south, east, and west and their relative position on a map. Provide access to geometry toolkits. Give students 2 minutes of quiet work time, followed by a partner and whole-class discussion.
Students with access to the digital materials can explore the applet.
Supports accessibility for: Conceptual processing; Memory
Student Facing
At a park, the slide is 5 meters east of the swings. Lin is standing 3 meters away from the slide.
-
Draw a diagram of the situation including a place where Lin could be.
-
How far away from the swings is Lin in your diagram?
-
Where are some other places Lin could be?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. If necessary, remind students of the directions north, south, east, and west and their relative position on a map. Provide access to geometry toolkits. Give students 2 minutes of quiet work time, followed by a partner and whole-class discussion.
Students with access to the digital materials can explore the applet.
Supports accessibility for: Conceptual processing; Memory
Student Facing
At a park, the slide is 5 meters east of the swings. Lin is standing 3 meters away from the slide.
-
Draw a diagram of the situation including a place where Lin could be.
- How far away from the swings is Lin in your diagram?
-
Where are some other places Lin could be?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students might assume that the swings, the slide, and Lin are all on a straight line, and that she must be 8 meters away. Ask these students if the problem tells us which direction Lin is from the slide.
Some students may confuse the type of compass discussed in the Launch and the type of compass discussed in the Activity Synthesis. Consider displaying a sample object or image of each of them and explain that the same name refers to two different tools.
Activity Synthesis
First, have students compare answers and share their reasoning with a partner until they reach an agreement.
Next, ask selected students to share their diagrams of where Lin is located. Discuss the following questions with the whole class:
- “Do we know for sure where Lin is?” (No, because we don’t know what direction she is from the swings.)
- “What shape is made by all the possible locations where Lin could be?” (a circle)
- “What is the closest Lin could be to the swings?” (2 m)
- “What is the farthest Lin could be away from the swings?” (8 m)
Consider using the applet at https://ggbm.at/qkHk6TpJ to show all the locations where Lin could be. Based on their work with drawing circles in a previous unit, some students may suggest that a compass could be used to draw all the possible locations where Lin could be. Consider having a student demonstrate how this could be done. If not mentioned by students, it is not necessary for the teacher to bring it up at this point.
7.2: How Long Is the Third Side? (15 minutes)
Activity
The purpose of this activity is for students to experience that the sum of the lengths of the two shorter sides of a triangle must be greater than the length of the longest side. Students continue working with the cardboard strips and fasteners from the previous lesson to see how many different triangles they can build given two of the three side lengths. In the Activity Synthesis, the possible triangles are arranged in a way that helps students see the unknown angle between two known side lengths as a hinge. This prepares students for using compasses to draw triangles with given side lengths. They also continue to work at recognizing when two triangles are identical copies that are oriented differently.
As students work, monitor for those who:
- find different lengths for the third side of the triangle
- use precise language to describe how the two side lengths can move in relation to each other
- make a connection to the circle of Lin’s possible positions from the previous activity
Launch
Arrange students in groups of 4. Distribute two sets of strips and fasteners (from the previous lesson) to each group. Give students 7–10 minutes of group work time, followed by a whole-class discussion.
If using the digital lesson, students will be familiar with this applet from the previous lesson.
Student Facing
Use the applet to answer the questions.
-
Build as many different triangles as you can that have one side length of 5 inches and one of 4 inches. Record the side lengths of each triangle you build.
-
Are there any other lengths that could be used for the third side of the triangle but aren't values of the sliders?
-
Are there any lengths that are values of the sliders but could not be used as the third side of the triangle?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 4. Distribute two sets of strips and fasteners (from the previous lesson) to each group. Give students 7–10 minutes of group work time, followed by a whole-class discussion.
If using the digital lesson, students will be familiar with this applet from the previous lesson.
Student Facing
Your teacher will give you some strips of different lengths and fasteners you can use to attach the corners.
-
Build as many different triangles as you can that have one side length of 5 inches and one of 4 inches. Record the side lengths of each triangle you build.
-
Are there any other lengths that could be used for the third side of the triangle but weren’t in your set?
-
Are there any lengths that were in your set but could not be used as the third side of the triangle?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Assuming you had access to strips of any length, and you used the 9-inch and 5-inch strips as the first two sides, complete the sentences:
- The third side can't be _____ inches or longer.
- The third side can't be _____ inches or shorter.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may think that there are more than 5 possible triangles they can build, because they don’t realize that some of the triangles they have listed are identical copies of other triangles on their list, with the side lengths written in a different order.
Some students may think that the third side of the triangle cannot be 4 or 5 inches, because then the triangle would have two sides of that length instead of the one asked for in the question. Explain that the triangle is acceptable as long as at least one side is 5 inches long and at least one side is 4 inches.
Some students may think that 8 is the longest the third side can be and 2 would be the shortest (if they were given a strip of that length), because they don’t realize that there could be fractional side lengths.
Activity Synthesis
Select previously identified groups to share a triangle they created. Establish whether each new triangle shared is the same as a triangle previously shared or is a different triangle. Collect one example of each possible triangle and display them for all to see, in order of increasing side length for the third side. Continue until students agree all possible triangles are displayed.

To help students generalize about all the possible triangles that could be built with sides 4 inches and 5 inches, ask questions like the following:
- “What do you notice about the triangles?”
- “Why was it impossible to use the 9 inch side to create a triangle?”
- “What is the longest the third side of the triangle could be?” (more than 8, but less than 9, e.g., 8.5, 8.75, 8.9)
- “What is the shortest the third side of the triangle could be?” (less than 2, but more than 1, e.g., 1.5, 1.25, 1.1)
- “What happens when the third side is 1 inch or 9 inches?” (You get a straight line instead of a triangle.)
Display a 5 inch strip fastened to a 4 inch strip for all to see. Demonstrate rotating the 4-inch strip around \(180^\circ\) to line up with each of the displayed triangles, as well as to show the idea that the third side could have a fractional side length. Invite students to share how this relates to the previous activity about Lin’s distance from the swings. (If we hold one strip fixed, then all the possible locations where the other strip could end form a circle.)
Design Principle(s): Optimize output (for generalization)
7.3: Swinging the Sides Around (15 minutes)
Activity
The purpose of this activity is to relate the process for building a triangle given 3 side lengths (using cardboard strips and metal fasteners) to the process for drawing a triangle given 3 side lengths (using a compass). Students use the cardboard strips as an informal compass for drawing all the possible locations where the given segments could end. They are reminded of their work with circles in a previous unit: that a circle is the set of all the points that are equally distant from a center point and that a compass is a useful tool, not just for drawing circles, but also for transferring lengths in general. This prepares them for using a compass to draw triangles in future lessons.
In this activity, students also consider what their drawing would look like if the two shorter sides were too short to make a triangle with the third given side length.
Left-handed students may find it easier to start with drawing the 3-inch circle on the left side of the 4-inch segment.
Launch
Arrange students in groups of 2.

Supports accessibility for: Memory; Conceptual processing
Student Facing
We'll explore a method for drawing a triangle that has three specific side lengths. Use the applet to answer the questions.
-
Follow these instructions to mark the possible endpoints of one side:
-
For now, ignore segment \(AC\) , the 3-inch side length on the left side
-

-
-
What shape have you drawn while moving \(BD\) around? Why? Which tool in your geometry toolkit can do something similiar?
-
Use your drawing to create two unique triangles, each with a base of length 4 inches and a side of length 3 inches. Use a different color to draw each triangle.
-
Repeat the previous instructions, letting segment \(AC\) be the 3-unit side length.
-
Using a third color, draw a point where the two traces intersect. Using this third color, draw a triangle with side lengths of 4 inches, 3 inches, and 3 inches.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Distribute one copy of the blackline master to each group. Make sure each group has one complete set of strips and fasteners from the previous activity. Provide access to geometry toolkits and compasses.
Tell students to take one 4-inch piece and two 3-inch pieces and connect them so that the 4-inch piece is in between the 3-inch pieces as seen in the image. If necessary, display the image for all to see. Students should not connect the 3-inch pieces to each other.
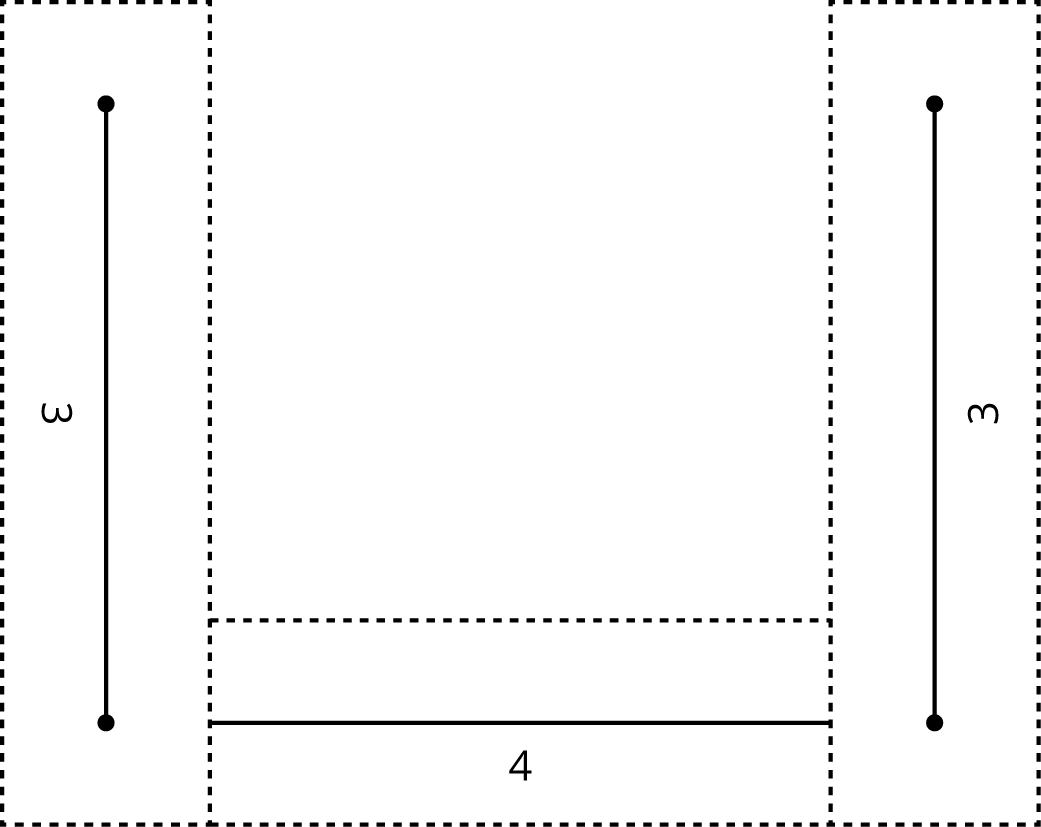
Explain to students that the sheet distributed to them is the 4-inch segment that is mentioned in the task statement and they will be drawing on that sheet.

Supports accessibility for: Memory; Conceptual processing
Student Facing
We’ll explore a method for drawing a triangle that has three specific side lengths. Your teacher will give you a piece of paper showing a 4-inch segment as well as some instructions for which strips to use and how to connect them.
-
Follow these instructions to mark the possible endpoints of one side:
- Put your 4-inch strip directly on top of the 4-inch segment on the piece of paper. Hold it in place.
- For now, ignore the 3-inch strip on the left side. Rotate it so that it is out of the way.
- In the 3-inch strip on the right side, put the tip of your pencil in the hole on the end that is not connected to anything. Use the pencil to move the strip around its hinge, drawing all the places where a 3-inch side could end.
- Remove the connected strips from your paper.
- What shape have you drawn while moving the 3-inch strip around? Why? Which tool in your geometry toolkit can do something similar?
- Use your drawing to create two unique triangles, each with a base of length 4 inches and a side of length 3 inches. Use a different color to draw each triangle.
- Reposition the strips on the paper so that the 4-inch strip is on top of the 4-inch segment again. In the 3-inch strip on the left side, put the tip of your pencil in the hole on the end that is not connected to anything. Use the pencil to move the strip around its hinge, drawing all the places where another 3-inch side could end.
- Using a third color, draw a point where the two marks intersect. Using this third color, draw a triangle with side lengths of 4 inches, 3 inches, and 3 inches.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Display a 4-inch strip connected to two 3-inch strips, positioned parallel to each other as pictured in the Launch. To help students connect the process of building with cardboard strips to drawing on paper, ask questions like:
- “If you want to build a triangle with these side lengths, how do you know at what angle to position the cardboard strips?” (Turn the sides until their unattached endpoints are touching.)
- “If you want to draw a triangle with these side length, how can you know at what angle to draw the sides?” (Find the point where both circles intersect.)
- “We have seen with the cardboard strips that an unknown angle works like a hinge. How is that represented in your drawing?” (with a circle centered on the endpoint of one segment and a radius the length of the other segment)
Select students to share their drawings with the class. To reinforce the patterns that students noticed in the previous activity, consider asking questions like these:
- “How many different triangles could we draw when we had only traced a circle on one side? Why?” (Lots of different triangles, because we were only using two of the given side lengths.)
- “What is the longest the third side could have been? And the shortest?” (Less the 7 inches; More than 1 inch)
- “How many different triangles could we draw once we had traced a circle on each side?” (It looked like there were 2 different triangles, but they are identical copies, so there’s really only 1 unique triangle.)
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
- When you are given side lengths and asked to draw a triangle, how can you get started? (Hold one length fixed and swing the other around in a circle.)
- If you draw one side of the triangle with circles (of the correct radius for the other two side lengths) on each end, what does it look like when it is impossible to make a triangle? (The two circles do not intersect, or they intersect at a point on the first line segment.)
- If you draw one side of the triangle with circles on each end, and the circles do cross, they will cross twice. Why do we say there’s only one possible triangle instead of two? (The two triangles are identical copies.)
7.4: Cool-down - Finishing Elena’s Triangles (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
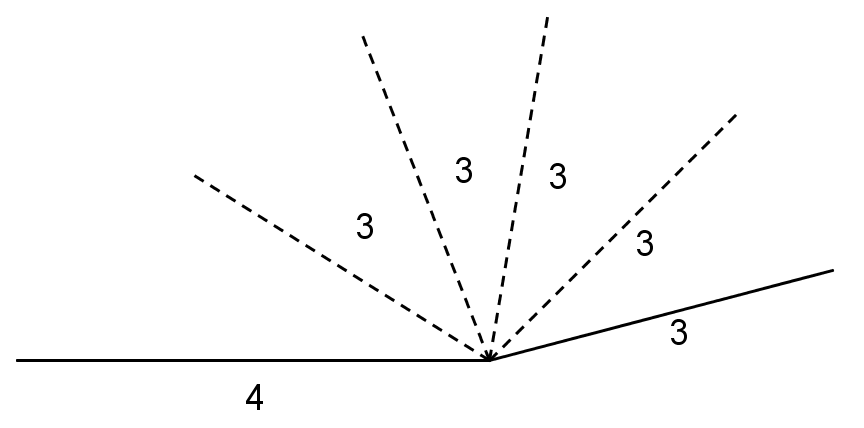
If we want to build a polygon with two given side lengths that share a vertex, we can think of them as being connected by a hinge that can be opened or closed:
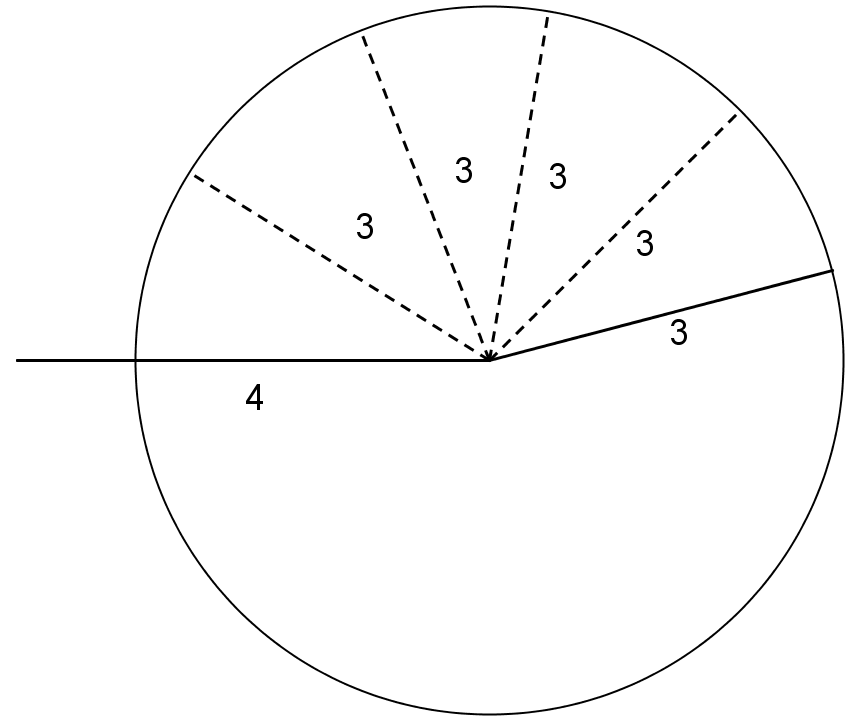
All of the possible positions of the endpoint of the moving side form a circle:
You may have noticed that sometimes it is not possible to build a polygon given a set of lengths. For example, if we have one really, really long segment and a bunch of short segments, we may not be able to connect them all up. Here's what happens if you try to make a triangle with side lengths 21, 4, and 2:
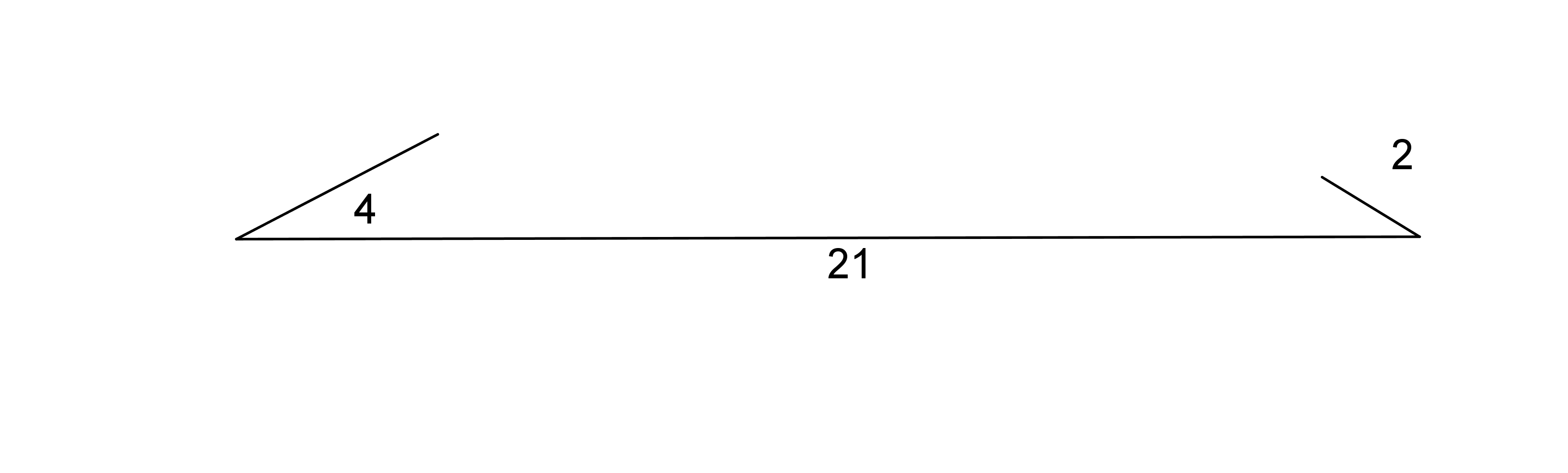
The short sides don't seem like they can meet up because they are too far away from each other.
If we draw circles of radius 4 and 2 on the endpoints of the side of length 21 to represent positions for the shorter sides, we can see that there are no places for the short sides that would allow them to meet up and form a triangle.
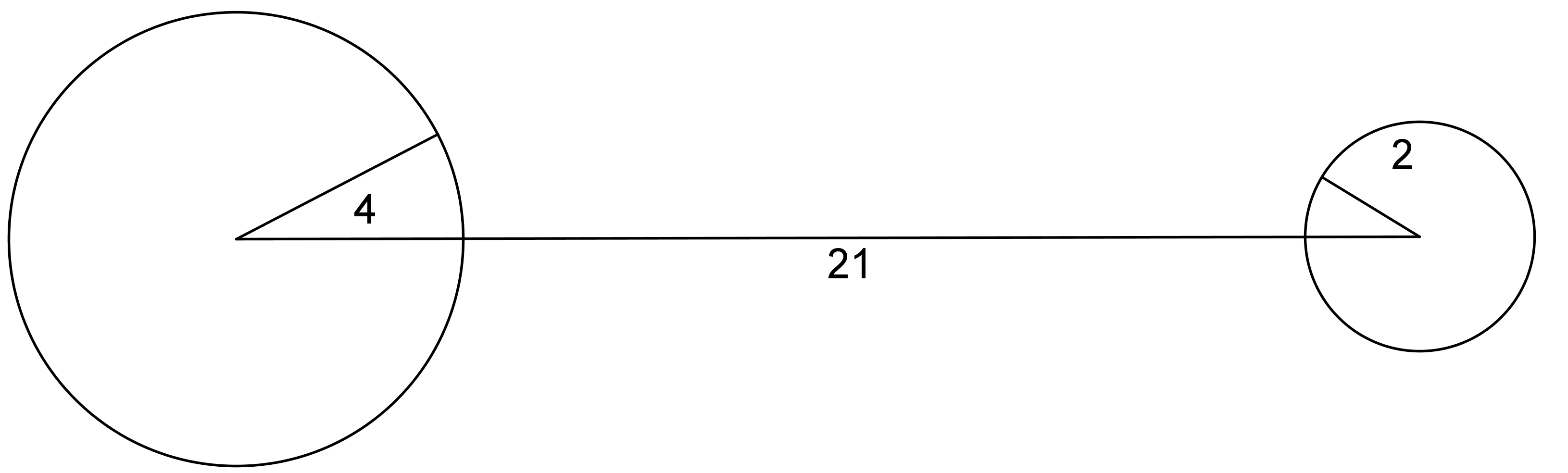
In general, the longest side length must be less than the sum of the other two side lengths. If not, we can’t make a triangle!
If we can make a triangle with three given side lengths, it turns out that the measures of the corresponding angles will always be the same. For example, if two triangles have side lengths 3, 4, and 5, they will have the same corresponding angle measures.