Lesson 4
Solving for Unknown Angles
4.1: True or False: Length Relationships (5 minutes)
Warm-up
The purpose of this warm-up is to have students express relationships between length measures with equations, in preparation for doing the same with angle measures in upcoming activities.
Launch
Remind students that we refer to a length of a segment by naming its endpoints. For example, \(AB\) means the length of the line segment from \(A\) to \(B\).
Display one problem at a time. Tell students to give a signal when they have decided if the equation is true or false. Give students 1 minute of quiet think time followed by a whole-class discussion.
Student Facing
Here are some line segments.

Decide if each of these equations is true or false. Be prepared to explain your reasoning.
\(CD+BC=BD\)
\(AB+BD=CD+AD\)
\(AC-AB=AB\)
\(BD-CD=AC-AB\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their reasoning for each equation. Record and display their responses for all to see. To involve more students in the conversation, consider asking:
- “Do you agree or disagree? Why?”
- “Who can restate ___’s reasoning in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
After each true equation, ask students if they could rely on the same reasoning to determine if other similar problems are equivalent. After each false equation, ask students how the problem could be changed to make the equation true.
4.2: Info Gap: Angle Finding (20 minutes)
Activity
The purpose of this info gap activity is for students to see how they can use different pieces of information to solve for an unknown angle measure in a multi-step problem. During the whole-class discussion, students are introduced to writing and solving equations to represent the relationships between angles.
The info gap structure requires students to make sense of problems by determining what information is necessary. This may take several rounds of discussion (MP1). Since there are many different pieces of information that could be used to solve the problem but are not given on the data card, consider using a variation on the typical info gap structure: Instead of the student with the problem card asking for specific pieces of information, the student with the data card chooses a piece of information to share, and the student with the problem card explains how they use that piece of information. If enough information hasn’t been given, the student with the data card chooses another piece of information to share.
You will need the blackline master for this activity. Here is the text of the cards for reference and planning:
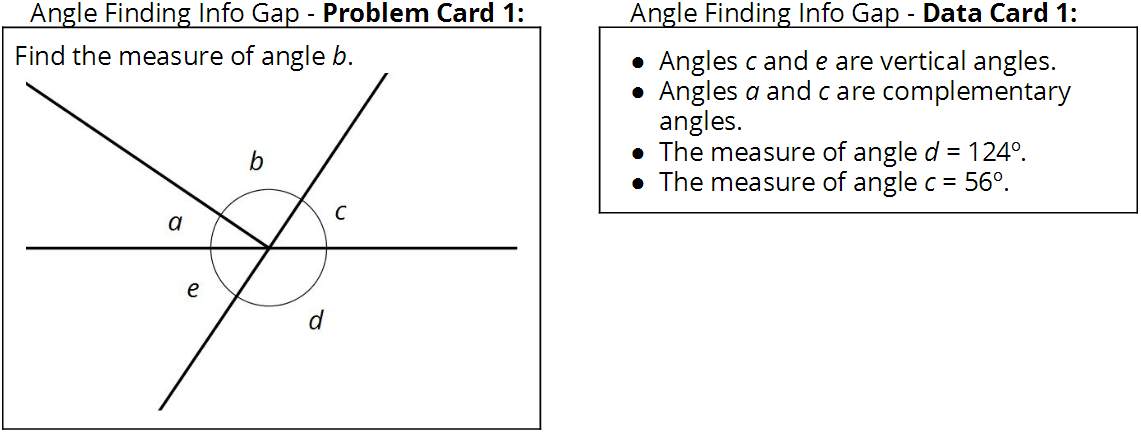
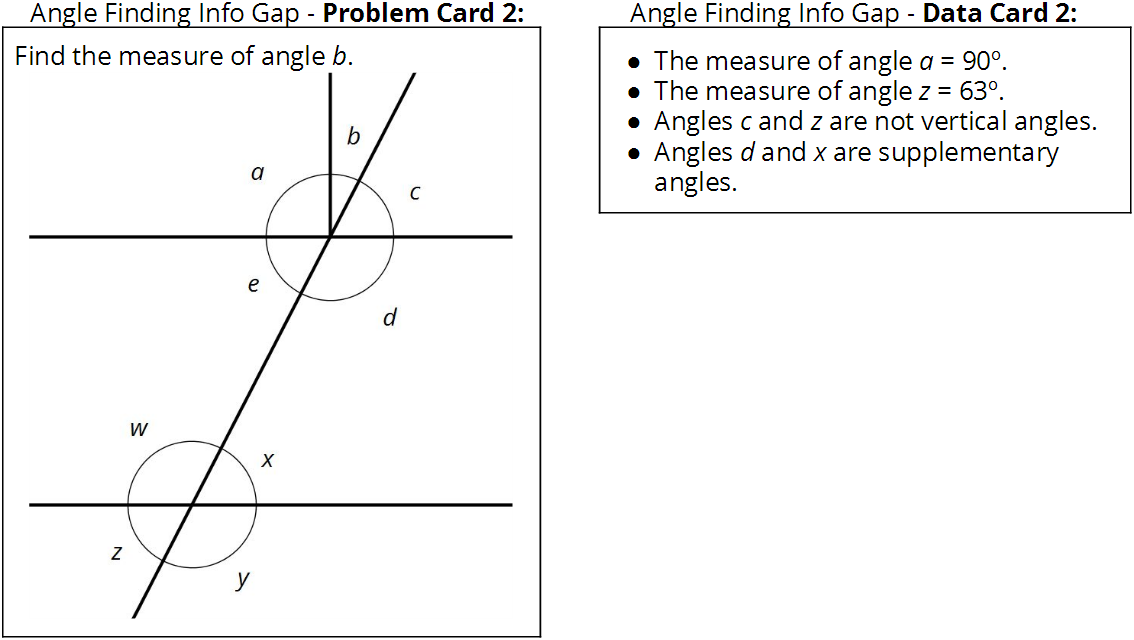
As students work, monitor for those who use different strategies or start with different pieces of information. Also, monitor for students who choose to show their reasoning by writing and solving equations.
Launch
If desired, explain this variation from the typical info gap: instead of the student with the problem card asking for each piece of information, the student with the data card chooses a piece of information to share. The student with the problem card still needs to explain how they can use each piece of information. If more information is needed to solve the problem, the student with the data card chooses another piece of information to share. Also, students need to listen to their partner carefully because they may be asked to explain their partner’s reasoning to the class.
Arrange students in groups of 2. Distribute a problem card to one student and a data card to the other student in each group.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Cultivate conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
For the second set of cards, students may struggle to find the connection between the lower half of the figure and the upper half. Remind them that supplementary angles do not need to be next to one another, but they can be.
Activity Synthesis
The goal of this discussion is for students to see that writing and solving equations is an efficient strategy to show their reasoning about multi-step angle problems.
For each problem, select a student who had the information card to share their partner’s reasoning. Record their reasoning using equations and display for all to see. Listen carefully and make sure the equation matches how they explain their reasoning. Here are some sample equations for the first problem.
solving for \(e\) given \(d\)
\(\begin{align} e + d &= 180 \\ e + 124 &= 180 \\ e &= 180 - 124 \\ e &= 56 \end{align}\)
solving for \(a\) given \(c\)
\(\begin{align} a + c &= 90 \\ a + 56 &= 90 \\ a &= 90 - 56 \\ a &= 34 \end{align}\)
solving for \(e\) given \(c\)
\(\displaystyle c = 56\)
\(\displaystyle e = c \\ e = 56\)
solving for \(b\) given that \(a\) and \(c\) are complementary
\(\displaystyle a + c = 90\)
\(\begin{align} a + b + c &= 180 \\ b + (a + c) &= 180 \\ b + 90 &= 180 \\ b &= 180 - 90 \\ b &= 90 \end{align}\)
Display the equations that represent different students’ strategies side by side and have students contrast the different methods, for example, the difference between how two students worked the problem if one was given the measure of angle \(d\) first but the other was given the measure of angle \(c\) first.
4.3: What’s the Match? (10 minutes)
Activity
The purpose of this activity is for students to match relationships between angles in a figure with equations that can represent those relationships. This prepares students for writing and solving equations that represent relationships between angles in the next lesson. As students explain their reasoning, monitor for students who use the appropriate vocabulary and language (i.e. vertical angles have equal measures, supplementary angles sum to 180 degrees, etc.).
Launch
Keep students in same groups. Give students 2–3 minutes of quiet work time followed by partner and whole-class discussions.
Student Facing
Match each figure to an equation that represents what is seen in the figure. For each match, explain how you know they are a match.
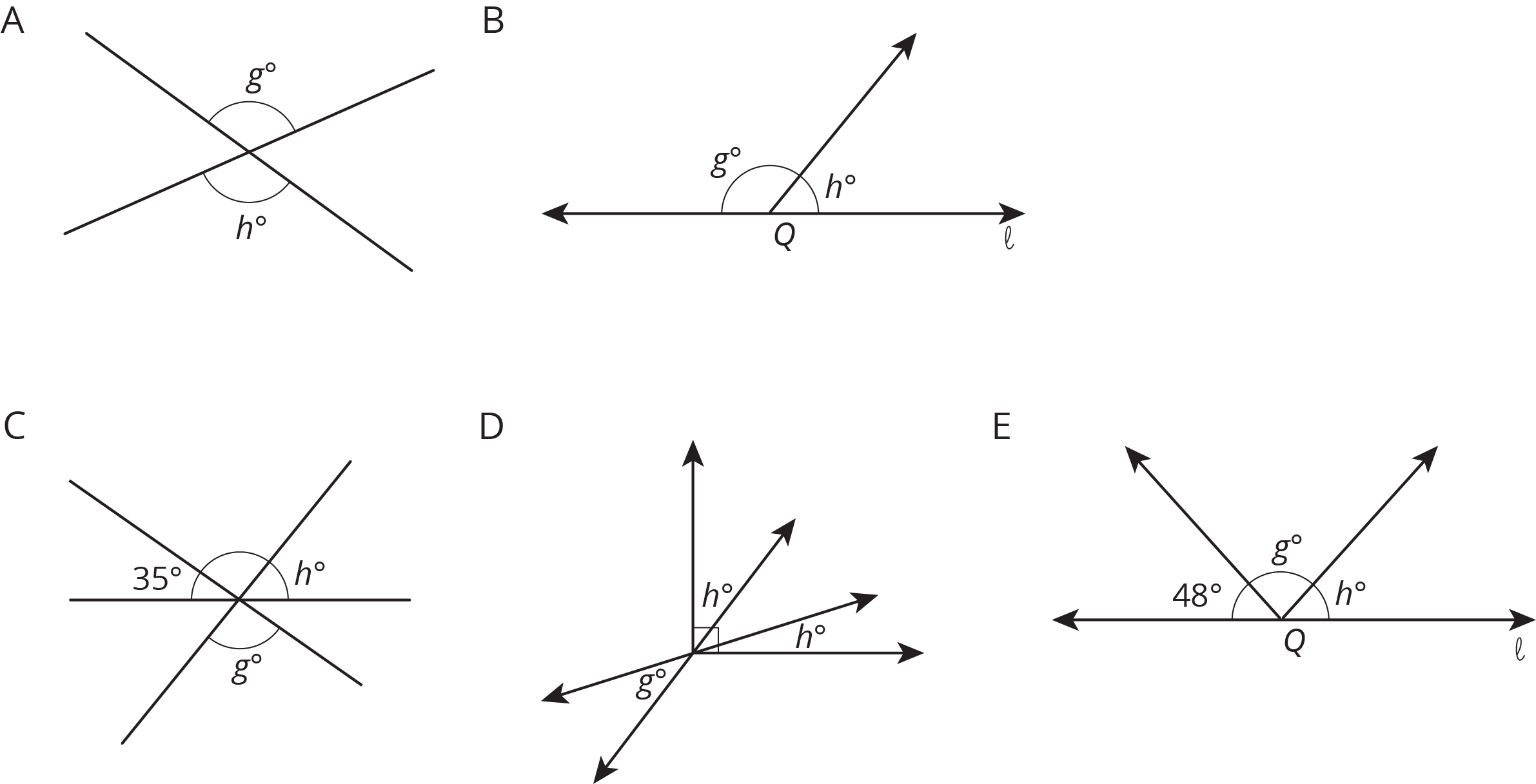
- \(g+h=180\)
- \(g=h\)
- \(2h+g=90\)
- \(g+h+48=180\)
-
\(g+h+35=180\)
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- What is the angle between the hour and minute hands of a clock at 3:00?
- You might think that the angle between the hour and minute hands at 2:20 is 60 degrees, but it is not! The hour hand has moved beyond the 2. Calculate the angle between the clock hands at 2:20.
- Find a time where the hour and minute hand are 40 degrees apart. (Assume that the time has a whole number of minutes.) Is there just one answer?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of this discussion is for students to articulate the angle relationships they noticed in each figure and equation. Display the figures for all to see. Select previously identified students to share their explanations for each figure. If not mentioned in students’ explanations be sure that students see the vertical, supplementary, straight, and right angle relationships in the figures.
Lesson Synthesis
Lesson Synthesis
- If you know that angles \(a\) and \(b\) are vertical, what equation could you use to represent this angle relationship? (\(a = b\))
- If you know that angles \(c\) and \(d\) are complementary, what equation could you use to represent this angle relationship? (\(c + d = 90\))
- If you know that angles \(e\) and \(f\) are supplementary, what equation could you use to represent this angle relationship? (\(e + f = 180\))
As the situations become more intricate, you can use equations to keep track of what you know so that you can revisit them when you learn more information.
4.4: Cool-down - Missing Circle Angles (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can write equations that represent relationships between angles.
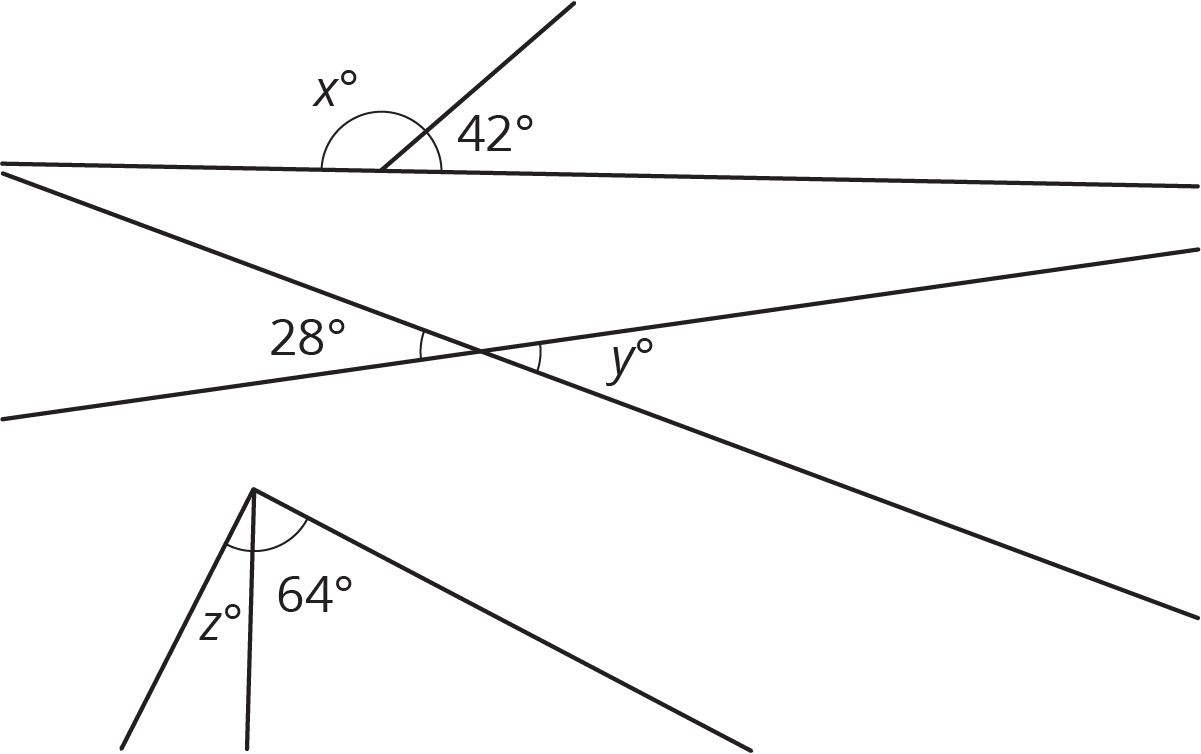
- The first pair of angles are supplementary, so \(x+42 = 180\).
- The second pair of angles are vertical angles, so \(y = 28\).
- Assuming the third pair of angles form a right angle, they are complementary, so \(z + 64 = 90\).