Lesson 8
Reasoning about Solving Equations (Part 2)
8.1: Equivalent to $2(x+3)$ (5 minutes)
Warm-up
Students worked with the distributive property with variables in grade 6 and with numbers in earlier grades. In order to understand the two ways of solving an equation of the form \(p(x+q)=r\) in the upcoming lessons, it is helpful to have some fluency with the distributive property.
Launch
Arrange students in groups of 2. Give 3 minutes of quiet work time and then invite students to share their responses with their partner, followed by a whole-class discussion.
Student Facing
Select all the expressions equivalent to \(2(x+3)\).
- \(2 \boldcdot (x+3) \)
- \((x + 3)2 \)
- \(2 \boldcdot x + 2 \boldcdot 3\)
- \(2 \boldcdot x + 3 \)
- \((2 \boldcdot x) + 3\)
- \((2 + x)3\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Focus specifically on why 1 and 3 are equivalent to lead into the next activity. You may also recall the warm-ups from prior lessons and ask if \(2(x+3)\) is equal to 10, or other numbers, how much is \(x+3\)?
Ask students to write another expression that is equivalent to \(2(x+3)\) (look for \(2x+6\)).
8.2: Either Or (15 minutes)
Activity
This activity continues the work of using a balanced hanger to develop strategies for solving equations. Students are presented with a balanced hanger and are asked to explain why each of two different equations could represent it. They are then asked to find the unknown weight. Note that no particular solution method is prescribed. Give students a chance to come up with a reasonable approach, and then use the synthesis to draw connections between the diagram and each of the two equations. Students notice the structure of equations and diagrams and find correspondences between them and between solution strategies.
Launch
Keep students in the same groups. Give 5–10 minutes of quiet work time and time to share their responses with a partner, followed by a whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Design Principle(s): Optimize output (for explanation); Cultivate conversation
Student Facing
-
Explain why either of these equations could represent this hanger:

\(14=2(x+3)\) or \(14=2x+6\)
- Find the weight of one circle. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Have one student present who did \(7=x+3\) first, and another student present who subtracted 6 first. If no one mentions one of these approaches, demonstrate it. Show how the hanger supports either approach. The finished work might look like this for the first equation:
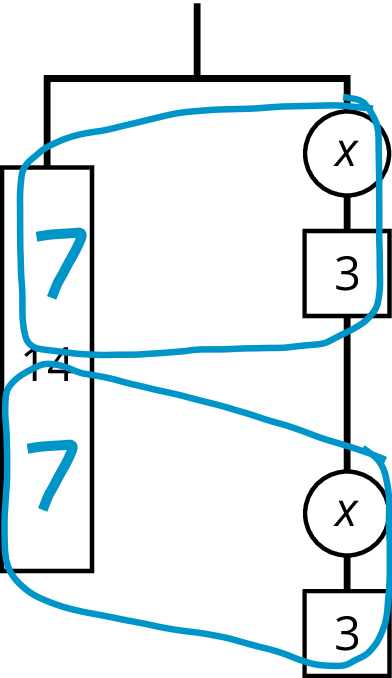
\(\begin {align} 14&=2(x+3) \\ 7&=x+3 \\ \end{align}\)
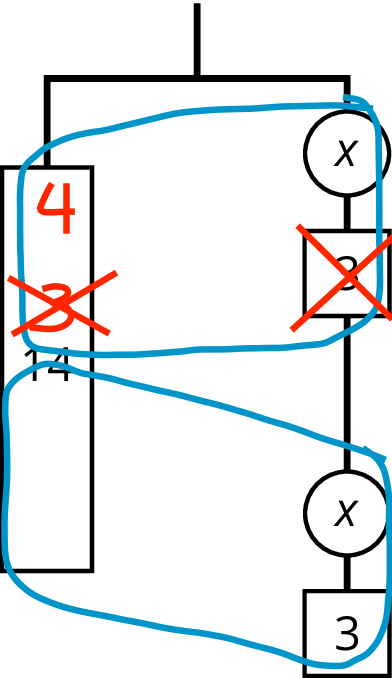
\(\begin {align} 7&=x+3 \\ 4&=x \\ \end{align}\)
For the second equation, rearrange the right side of the hanger, first, so that 2 \(x\)’s are on the top and 6 units of weight are on the bottom. Then, cross off 6 from each side and divide each side by 2. Show this side by side with “doing the same thing to each side” of the equation.
8.3: Use Hangers to Understand Equation Solving, Again (15 minutes)
Activity
The first question is straightforward since each diagram uses a different letter, but it’s there to make sure students start with \(p(x+q)=r\). If some want to rewrite as \(px+pq=r\) first, that’s great. We want some to do that but others to divide both sides by \(p\) first. Monitor for students who take each approach.
Launch
Keep students in the same groups. Give 5–10 minutes of quiet work time and time to share their responses with a partner, followed by a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Here are some balanced hangers. Each piece is labeled with its weight.
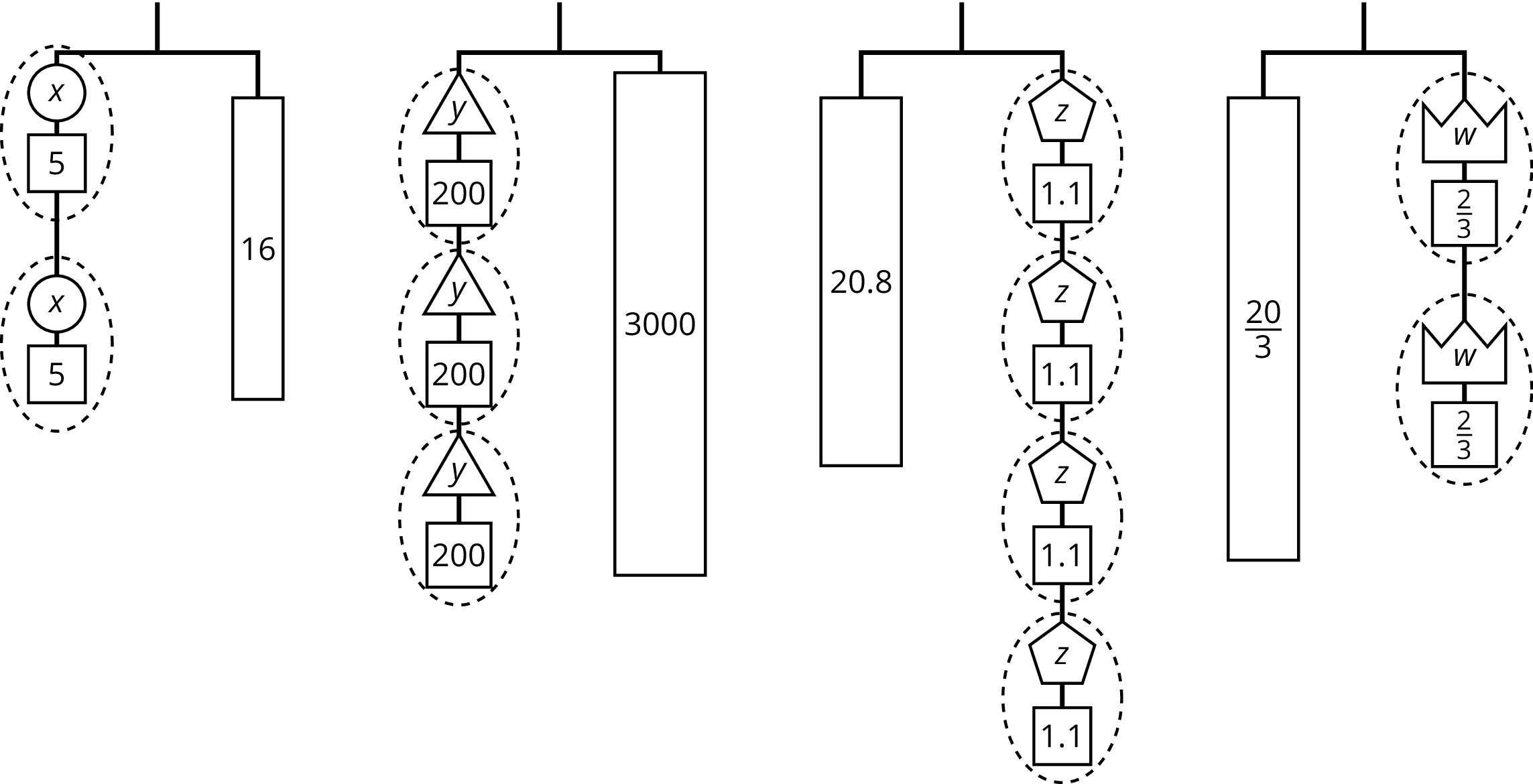
For each diagram:
- Assign one of these equations to each hanger:
\(2(x+5)=16\)
\(3(y+200)=3\!,000\)
\(20.8=4(z+1.1)\)
\(\frac{20}{3}=2\left(w+\frac23\right)\)
- Explain how to figure out the weight of a piece labeled with a letter by reasoning about the diagram.
- Explain how to figure out the weight of a piece labeled with a letter by reasoning about the equation.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select one hanger for which one student divided by \(p\) first and another student distributed \(p\) first. Display the two solution methods side by side, along with the hanger.
Design Principle(s): Cultivate conversation
Lesson Synthesis
Lesson Synthesis
Display the equation \(4(x+7)=40\). Ask one partner to solve by dividing first and the other to solve by distributing first. Then, check that they got the same solution and that it makes the equation true. If they get stuck, encourage them to draw a diagram to represent the equation.
8.4: Cool-down - Solve Another Equation (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The balanced hanger shows 3 equal, unknown weights and 3 2-unit weights on the left and an 18-unit weight on the right.
There are 3 unknown weights plus 6 units of weight on the left. We could represent this balanced hanger with an equation and solve the equation the same way we did before.
\(\begin {align} 3x+6&=18 \\ 3x&=12 \\ x&=4 \\ \end{align}\)
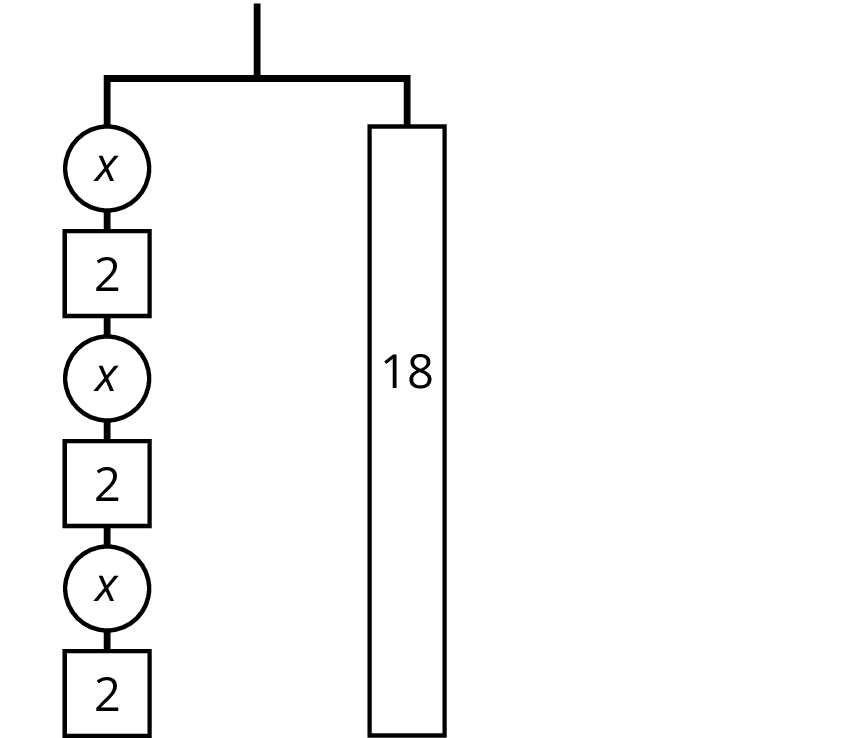
Since there are 3 groups of \(x+2\) on the left, we could represent this hanger with a different equation: \(3(x+2)=18\).
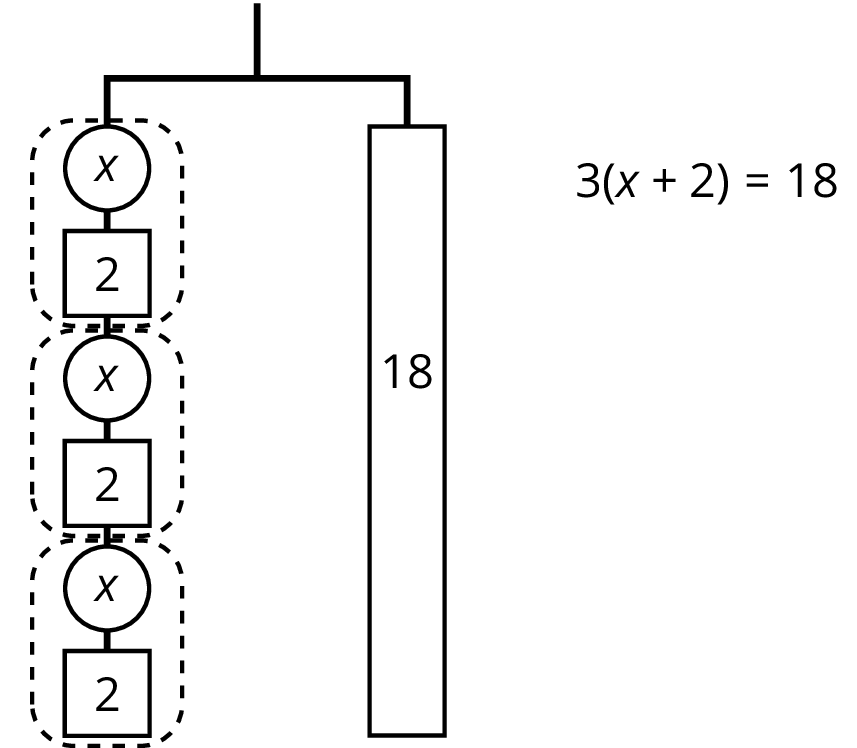
The two sides of the hanger balance with these weights: 3 groups of \(x+2\) on one side, and 18, or 3 groups of 6, on the other side.
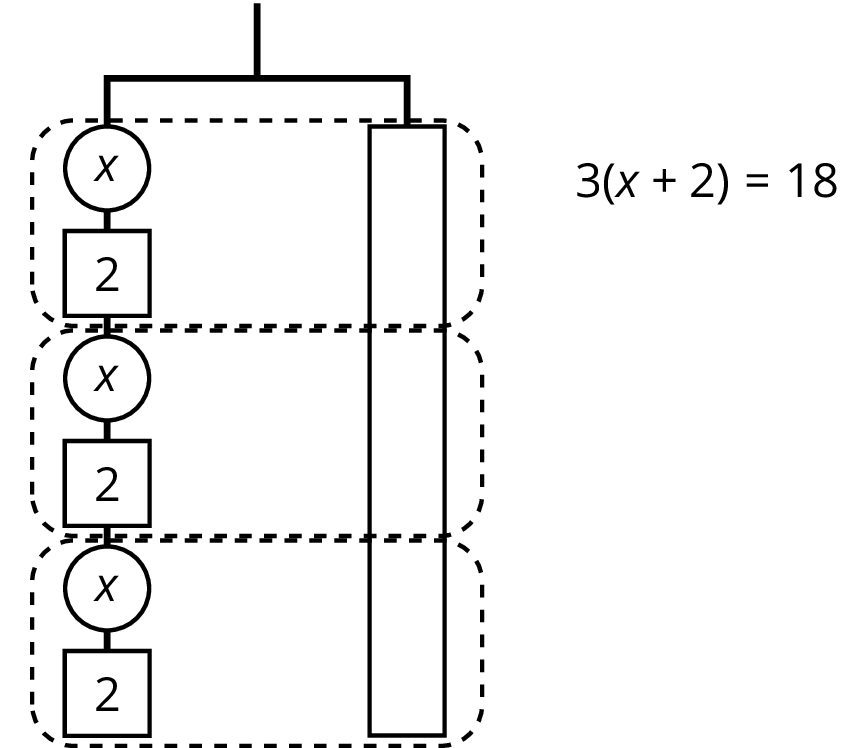
The two sides of the hanger will balance with \(\frac13\) of the weight on each side: \(\frac13 \boldcdot 3(x+2) = \frac13 \boldcdot 18\).
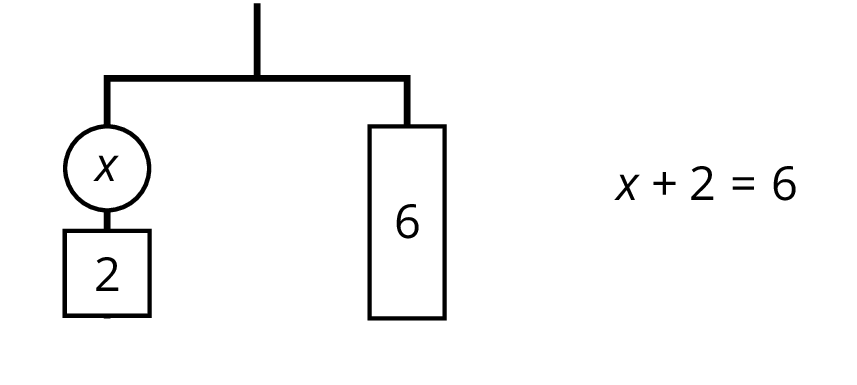
We can remove 2 units of weight from each side, and the hanger will stay balanced. This is the same as subtracting 2 from each side of the equation.
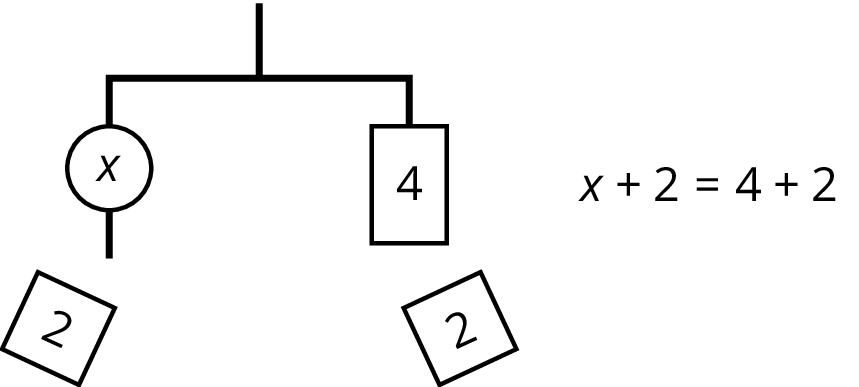
An equation for the new balanced hanger is \(x=4\). This gives the solution to the original equation.
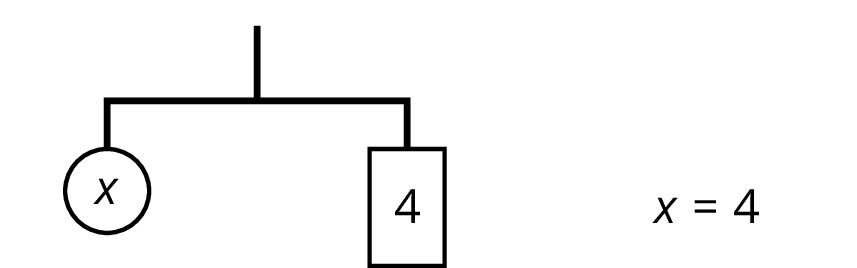
Here is a concise way to write the steps above:
\(\begin{align} 3(x+2) &= 18 \\ x + 2 &= 6 & \text{after multiplying each side by } \tfrac13 \\ x &= 4 & \text{after subtracting 2 from each side} \\ \end{align} \)