Lesson 13
Reintroducing Inequalities
13.1: Greater Than One (5 minutes)
Warm-up
The purpose of this activity is for students to substitute values into an inequality and check to see if each value satisfies the inequality based on a number line representation. This is the first opportunity (of many to come) to practice this type of substitution with inequalities.
Launch
Arrange students in groups of 2. Since it may have been a while since students encountered this notation, remind students that \(x>1\) is read “\(x\) is greater than 1.” Give students 2 minutes of quiet work time followed by 1 minute to share their responses with a partner. During the partner discussion, tell students to compare their answers for the first question and see if they agree with their partner’s chosen values for the second question. Follow with a whole-class discussion.
Student Facing
The number line shows values of \(x\) that make the inequality \(x>1\) true.
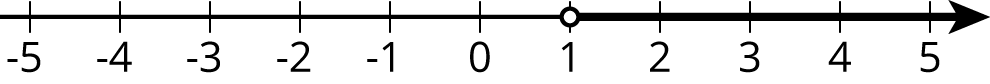
-
Select all the values of \(x\) from this list that make the inequality \(x>1\) true.
-
3
-
-3
-
1
-
700
-
1.05
-
- Name two more values of \(x\) that are solutions to the inequality.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may think 700 is not a solution to \(x > 1.\) Tell students that since there is an arrow at the end of the dark line, it includes all values that would fall on that line, even the ones not shown.
Activity Synthesis
Ask a few students to share their responses for the last question. After each student shares, ask the class whether they agree or disagree. If students focus solely on the number line representation, be sure to tell them that to test whether a value makes an inequality true, you can substitute the value for the variable. Highlight the fact that “greater than 1” does not include 1.
Here are some questions for discussion:
- What does the open circle at 1 mean? (It means 1 is not included.)
- Is 1 a solution to the inequality \(x>1\)?
13.2: The Roller Coaster (15 minutes)
Activity
The purpose of this activity is to remind students that the symbol < is read “is less than” and the symbol > is read “is greater than.” Also, remind students of the use of an open circle or closed circle to indicate that the boundary point is included. Then, the symbols \(\leq\) and \(\geq\) are introduced.
Monitor for students who express the answer to the last question using words or using symbols. The responses to the last question will be used to introduce the new notation.
Launch
Allow students 5–10 minutes quiet work time and time to share their responses with a partner, followed by a whole-class discussion.
Supports accessibility for: Language
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Student Facing
A sign next to a roller coaster at an amusement park says, “You must be at least 60 inches tall to ride.” Noah is happy to know that he is tall enough to ride.

- Noah is \(x\) inches tall. Which of the following can be true: \(x > 60\), \(x = 60\), or \(x < 60\)? Explain how you know.
- Noah’s friend is 2 inches shorter than Noah. Can you tell if Noah’s friend is tall enough to go on the ride? Explain or show your reasoning.
- List one possible height for Noah that means that his friend is tall enough to go on the ride, and another that means that his friend is too short for the ride.
-
On the number line below, show all the possible heights that Noah’s friend could be.
- Noah's friend is \(y\) inches tall. Use \(y\) and any of the symbols \(<\), \(=\), \(>\) to express this height.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students are having trouble interpreting the first three questions or articulating their responses, encourage them to make use of the number line that appears in question 4.
Activity Synthesis
Ask selected students to share their response to the last question. They are likely to write something like “\(y=58\) or \(y>58\).” The < and > symbols are not enough to capture what we need here with a single mathematical statement. In grade 6, students saw graphs of inequalities using open and closed circles. Now, we can introduce new symbols \(\leq\) and \(\geq\), that mean “less than or equal to” and “greater than or equal to.”
13.3: Is the Inequality True or False? (15 minutes)
Activity
The purpose of this task is for students to interpret the notation \(<\), \(>\), \(\leq\), and \(\geq\) to evaluate whether different values make an inequality true. It is not expected that students will solve the inequalities generally. The work in this activity sets students up for success in later lessons when they test points to determine the direction of the inequality in the process of solving.
Notice students who use the following approaches:
- Substituting a value in for \(x\), evaluating the expression, thinking about whether the statement is true. For example, “Is -300 less than 75? Yes, so this is true.”
- Drawing a number line for each inequality and using it to reason about different values.
Launch
Keep students in the same groups. Give 5–10 minutes quiet and partner work time followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
The table shows four inequalities and four possible values for \(x\). Decide whether each value makes each inequality true, and complete the table with “true” or “false.” Discuss your thinking with your partner. If you disagree, work to reach an agreement.
| \(x\) | 0 | 100 | -100 | 25 |
|---|---|---|---|---|
| \(x \leq 25\) | ||||
| \(100 < 4x\) | ||||
| \(\text-3x > \text-75\) | ||||
| \(10 \geq 35 - x\) |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Find an example of in inequality used in the real world and describe it using a number line.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students who try to apply what they know about solving equations to solve the inequalities algebraically may come up with incorrect solutions. For instance, \(100 < 4x\) may at first glance look equivalent to \(x < 25\), since the “less than” sign appears. Students may incorrectly think that \(\text-3x > \text-75\) is equivalent to \(x > 25\). Ask these students, for example, what the solution to \(100 = 4x\) means (25 is the value of \(x\) that makes \(4x\) equal to 100). Then encourage these students to test values like 24 and 26 to see whether they are solutions to \(100 < 4x\). This will be covered in greater detail in a later lesson, so this understanding does not need to be solidified at this time.
Activity Synthesis
The purpose of the discussion is to note the consequences of an inequality using \(\leq\) versus <, and \(\geq\) versus >. Direct students’ attention to \(100 < 4x\) and \(10 \geq 35 - x\). Substituting 25 for \(x\) in each of these inequalities gives \(100 < 100\), which is false, and \(10 \geq 10\), which is true. The key distinction is that \(\geq\) and \(\leq\) inequalities are considered true when both sides are equal, whereas < and > inequalities are considered false when both sides are equal. Ask students to present different strategies for determining whether a value makes an inequality true. Ask whether students were surprised by or initially incorrect about any of the answers. Emphasize that substituting a value in for \(x\), and thinking about whether the resulting inequality is saying something true, is the most direct way to check whether the value is a solution.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
By the end of this lesson, students should be able to interpret the symbols \(\geq\) and \(\leq\) and be able to test whether a given value makes an inequality true. Ask students to write an equality to which -5 is a solution, then trade with their partner to see if their partner agrees.
13.4: Cool-down - Some Values, All Values (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We use inequalities to describe a range of numbers. In many places, you are allowed to get a driver’s license when you are at least 16 years old. When checking if someone is old enough to get a license, we want to know if their age is at least 16. If \(h\) is the age of a person, then we can check if they are allowed to get a driver’s license by checking if their age makes the inequality \(h>16\) (they are older than 16) or the equation \(h=16\) (they are 16) true. The symbol \(\geq\), pronounced “greater than or equal to,” combines these two cases and we can just check if \(h \geq 16\) (their age is greater than or equal to 16). The inequality \(h \geq 16\) can be represented on a number line:
