Lesson 15

Efficiently Solving Inequalities

View Student Lesson

15.1: Lots of Negatives (5 minutes)

CCSS Standards


Building Towards

Warm-up

This warm-up primes students for inequalities that include variables with negative coefficients without context. Students first predict a solution set, and then are given some values to test so that the solution emerges. Do not formalize a procedure for “flipping the inequality” when multiplying by a negative. Look for students who predict solution sets that are incorrect because of the sign.

Launch

Give students 3 minutes of quiet work time followed by a whole-class discussion.

Student Facing

Here is an inequality: \(\text-x \geq \text-4\).

  1. Predict what you think the solutions on the number line will look like.
     
  2. Select all the values that are solutions to \(\text-x \geq \text-4\):
    1. 3
    2. -3
    3. 4
    4. -4
    5. 4.001
    6. -4.001
  3. Graph the solutions to the inequality on the number line:
    Blank number line, 11 evenly spaced tick marks, no labels.

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

The purpose of the discussion is to highlight how negatives in the inequality sometimes make it hard to predict what the solutions will be. (It is important to reason carefully by first determining the value for which both sides are equal and then testing points to determine which on side of that value the solutions lie.) Select students to share how their predictions differed from their final solutions. Consider asking how the solutions to \(\text-x \geq \text-4\) are different from the solutions to \(x \geq 4\). (The solutions go in the opposite direction on the number line.)

15.2: Inequalities with Tables (15 minutes)

CCSS Standards


Building Towards

Activity

The purpose of this activity is for students to get a visual feel for the relationship between an unsimplified inequality (\(x-3 > \text-2\)) and its solution (\(x > 1\)). The tables suggest a way for students to see why the values of \(x\) that satisfy \(x-3 > \text-2\) should also satisfy \(x > 1\). Graphing solutions on the number line reinforces this connection. The second and third questions, taken together, demonstrate how a negative coefficient can make the solutions to an inequality go “the other way.” The work in this activity suggests a procedure for solving inequalities: solve the corresponding equation, then test a number on either side. But the purpose of this activity is not to teach students a procedure, but rather to provide underlying knowledge and experience.

Launch

A potentially challenging aspect of this task is that students must consider the two rows of a table at different times and relate the values in the table to solutions of an inequality. Consider displaying a table like this for all to see, and then asking some questions about it:

\(x\) -4 -3 -2 -1 0 1 2 3 4
\(x+2\) -2 -1 0 1 2 3 4 5 6

After students have had a chance to look at the table, ask them some familiarizing questions:

  • How are the numbers in the top row and bottom row related?
  • Think about the equation \(x+2=\text-2\). What value of \(x\) makes this true? Where do you see that in the table?
  • Think about the inequality \(x+2>3\). What values of \(x\) make this true? Where do you see that in the table?

Give 5–10 minutes of quiet work time to complete the tables and questions followed by a whole-class discussion. Depending on the needs of your class, you might instruct students to pause after each question for discussion before continuing with the next question.

Action and Expression: Internalize Executive Functions. Chunk this task into more manageable parts to support students who benefit from support with organizational skills in problem solving. For example, present one question at a time and monitor students to ensure they are making progress throughout the activity. Consider pausing after the first question for a brief class discussion before moving on.
Supports accessibility for: Organization; Attention

Student Facing

  1. Let's investigate the inequality \(x-3>\text-2\).

    \(x\) -4 -3 -2 -1 0 1 2 3 4
    \(x-3\) -7 -5 -1 1
    1. Complete the table.
    2. For which values of \(x\) is it true that \(x - 3 = \text-2\)?
    3. For which values of \(x\) is it true that \(x - 3 > \text-2\)?
    4. Graph the solutions to \(x - 3 > \text-2\) on the number line:
      Blank number line, 11 evenly spaced tick marks, no labels.

  2. Here is an inequality: \(2x<6\).

    1. Predict which values of \(x\) will make the inequality \(2x < 6\) true.

    2. Complete the table. Does it match your prediction?

      \(x\) -4 -3 -2 -1 0 1 2 3 4
      \(2x\)

    3. Graph the solutions to \(2x < 6\) on the number line:

      Blank number line, 11 evenly spaced tick marks, no labels.

  3. Here is an inequality: \(\text-2x<6\).

    1. Predict which values of \(x\) will make the inequality \(\text-2x < 6\) true.

    2. Complete the table. Does it match your prediction?

      \(x\) -4 -3 -2 -1 0 1 2 3 4
      \(\text-2x\)

    3. Graph the solutions to \(\text-2x < 6\) on the number line:
      Blank number line, 11 evenly spaced tick marks, no labels.
    4. How are the solutions to \(2x<6\) different from the solutions to \(\text-2x<6\)?

Student Response

For access, consult one of our IM Certified Partners.

Anticipated Misconceptions

Some students may answer \(x > 2\) for the first question, since that is the place where the value of \(x-3\) first surpasses the number -2. Remind these students that there are values between 1 and 2. Ask them whether 1.1 is a solution, for example.

Some students may graph only whole-number solutions. Ask these students to think about whether values in between whole numbers are also solutions.

Activity Synthesis

The main take-away is that solving the associated equation to an inequality gives the value that is the boundary between solutions and non-solutions. In this activity, students have a table to check on which side of the boundary are solutions and which side are not solutions. In order to transition to the next activity, ask students whether they need to complete an entire table to test on which side of the boundary the solutions are. The goal is to get students to understand that they only need to test one number. If that number is a solution, then all points on the same side of the boundary are solutions. If the point is not a solution, then the solutions are all the points on the other side of the boundary. The next activity will give students an opportunity to apply this insight and start to articulate such a procedure.

Resist the temptation to summarize the last two problems into a procedure like “whenever you multiply or divide by a negative, flip the inequality.”

15.3: Which Side are the Solutions? (15 minutes)

CCSS Standards


Building Towards

Routines and Materials


Instructional Routines

Activity

In the previous activity, students saw that solving the equation associated with an inequality gives a boundary point that separates values that make the inequality true from values that make the inequality false. This activity builds on that understanding to solidify a process for solving inequalities: first solve the associated equation to find the boundary point, then test a value to determine on which side of that boundary the solutions lie. The first two questions offer more scaffolding, and the last two questions simply give an inequality and ask students to solve and graph.

Launch

Arrange students in groups of 2. Give 5–10 minutes of quiet work time, time to share their responses and reasoning with a partner, and follow with a whole-class discussion. 

Representation: Internalize Comprehension. Activate or supply background knowledge. Allow students to use calculators to ensure inclusive participation in the activity.
Supports accessibility for: Memory; Conceptual processing

Student Facing

  1. Let’s investigate \(\text-4x + 5 \geq 25\).
    1. Solve \(\text-4x+5 = 25\).
    2. Is \(\text-4x + 5 \geq 25\) true when \(x\) is 0? What about when \(x\) is 7? What about when \(x\) is -7?
    3. Graph the solutions to \(\text-4x + 5 \geq 25\) on the number line.
      Blank number line, 11 evenly spaced tick marks, no labels.
  2. Let's investigate \(\frac{4}{3}x+3 < \frac{23}{3}\).
    1. Solve \(\frac43x+3 = \frac{23}{3}\).
    2. Is \(\frac{4}{3}x+3 < \frac{23}{3}\) true when \(x\) is 0?

    3. Graph the solutions to \(\frac{4}{3}x+3 < \frac{23}{3}\) on the number line.

      Blank number line, 11 evenly spaced tick marks, no labels.
  3. Solve the inequality \(3(x+4) > 17.4\) and graph the solutions on the number line.
    Blank number line, 11 evenly spaced tick marks, no labels.
  4. Solve the inequality \(\text-3\left(x-\frac43\right) \leq 6\) and graph the solutions on the number line.
    Blank number line, 11 evenly spaced tick marks, no labels.

Student Response

For access, consult one of our IM Certified Partners.

Student Facing

Are you ready for more?

Write at least three different inequalities whose solution is \(x > \text-10\). Find one with \(x\) on the left side that uses a \(<\).

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

For each question, ask one student to demonstrate and explain their process for solving the inequality. For each, highlight the moment when they find the boundary value (the solution to the related equation) and then when they test one or more numbers on either side to decide which side has values that make the inequality true.

Representing, Conversing: MLR7 Compare and Connect. During the whole-class discussion, ask students to discuss with their partner, what is the same and what is different between the demonstrated processes for solving each inequality. To call students’ attention to the different ways the boundary values were determined, ask students, “Which numbers can be used to check the direction of the solution?” This will help students produce language, including symbols, common to inequalities as they reason about procedures for solving inequalities.
Design Principle(s): Maximize meta-awareness; Cultivate conversation

Lesson Synthesis

Lesson Synthesis

By the time students have finished this lesson, they should have a variety of methods for solving inequalities, all of which involve some kind of final decision about the direction of inequality. Students will have had some summative practice with this in the final activity and the cool-down.

Ask students to consider, “What if someone asked for your help with how to solve inequalities? What would you tell them? How would you describe to someone how to solve any inequality?” Ask them to either write this down or share their thoughts with their partner. Consider creating a persistent display showing the procedure using language the class develops, along with an example.

15.4: Cool-down - Testing for Solutions (5 minutes)

CCSS Standards


Addressing

Cool-Down

For access, consult one of our IM Certified Partners.

Student Lesson Summary

Student Facing

Here is an inequality: \(3(10-2x) < 18\). The solution to this inequality is all the values you could use in place of \(x\) to make the inequality true.

In order to solve this, we can first solve the related equation \(3(10-2x) = 18\) to get the solution \(x = 2\). That means 2 is the boundary between values of \(x\) that make the inequality true and values that make the inequality false.

To solve the inequality, we can check numbers greater than 2 and less than 2 and see which ones make the inequality true.

Let’s check a number that is greater than 2: \(x= 5\). Replacing \(x\) with 5 in the inequality, we get \(3(10-2 \boldcdot 5) < 18\) or just \(0 < 18\). This is true, so \(x=5\) is a solution. This means that all values greater than 2 make the inequality true. We can write the solutions as \(x > 2\) and also represent the solutions on a number line:

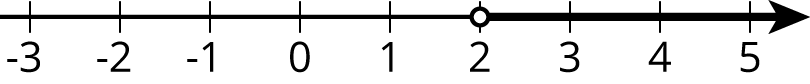
Number line, labeled negative 3 to 5 by ones.  An arrow begins at 2, open circle, extends to the right.

Notice that 2 itself is not a solution because it's the value of \(x\) that makes \(3(10-2x)\) ​equal to 18, and so it does not make \(3(10-2x) < 18\) true.

For confirmation that we found the correct solution, we can also test a value that is less than 2. If we test \(x=0\), we get \(3(10-2 \boldcdot 0) < 18\) or just \(30 < 18\). This is false, so \(x = 0\) and all values of \(x\) that are less than 2 are not solutions.